Mô hình phân lớp Naive Bayes

Bài đăng này đã không được cập nhật trong 4 năm

1. Mô hình phân lớp là gì?

Một mô hình phân lớp là một mô hình Machine Learning dùng để phân loại các vật mẫu dựa trên các đặc tính đã xác định.

2. Mô hình phân lớp Naive Bayes

Naive Bayes là một thuật toán phân lớp được mô hình hoá dựa trên định lý Bayes trong xác suất thống kê: , trong đó:

P(y|X) gọi là posterior probability: xác suất của mục tiêu y với điều kiện có đặc trưng X
P(X|y) gọi là likelihood: xác suất của đặc trưng X khi đã biết mục tiêu y
P(y) gọi là prior probability của mục tiêu y
P(X) gọi là prior probability của đặc trưng X

Ở đây, X là vector các đặc trưng, có thể viết dưới dạng:

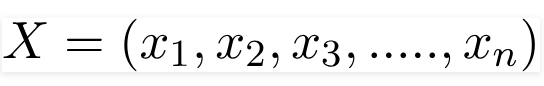
Khi đó, đẳng thức Bayes trở thành:

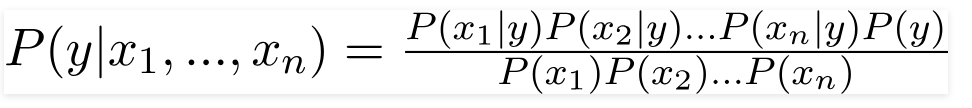
Trong mô hình Naive Bayes, có hai giả thiết được đặt ra:

Các đặc trưng đưa vào mô hình là độc lập với nhau. Tức là sự thay đổi giá trị của một đặc trưng không ảnh hưởng đến các đặc trưng còn lại.
Các đặc trưng đưa vào mô hình có ảnh hưởng ngang nhau đối với đầu ra mục tiêu.

Khi đó, kết quả mục tiêu y để P(y|X) đạt cực đại trở thành:

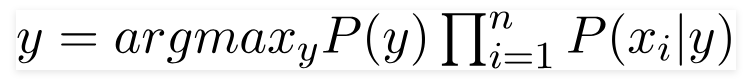
Chính vì hai giả thiết gần như không tồn tại trong thực tế trên, mô hình này mới được gọi là naive (ngây thơ). Tuy nhiên, chính sự đơn giản của nó với việc dự đoán rất nhanh kết quả đầu ra khiến nó được sử dụng rất nhiều trong thực tế trên những bộ dữ liệu lớn, đem lại kết quả khả quan. Một vài ứng dụng của Naive Bayes có thể kể đến như: lọc thư rác, phân loại văn bản, dự đoán sắc thái văn bản, ...

3. Một số kiểu mô hình Naive Bayes

3.1. Multinomial Naive Bayes

Mô hình này chủ yếu được sử dụng trong phân loại văn bản. Đặc trưng đầu vào ở đây chính là tần suất xuất hiện của từ trong văn bản đó.

3.2. Bernoulli Naive Bayes

Mô hình này được sử dụng khi các đặc trưng đầu vào chỉ nhận giá trị nhị phân 0 hoặc 1 (phân bố Bernoulli).

3.3. Gaussian Naive Bayes

Khi các đặc trưng nhận giá trị liên tục, ta giả sử các đặc trưng đó có phân phối Gaussian. Khi đó, likelihood sẽ có dạng:

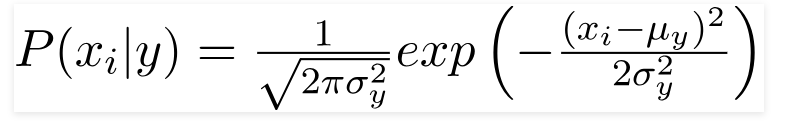
4. Ví dụ

Xét một bộ dữ liệu đơn giản về việc đi làm muộn của một bạn nhân viên. Bộ dữ liệu được biểu diễn dạng bảng dưới đây:

	Giờ dậy (x1)	Sức khoẻ (x2)	Thời tiết (x3)	Đi muộn (y)
1	Sớm	Tốt	Nắng	Không
2	Sớm	Xấu	Mưa	Không
3	Bình thường	Tốt	Nắng	Có
4	Muộn	Xấu	Nắng	Có
5	Sớm	Xấu	Nhiều mây	Không
6	Bình thường	Xấu	Nhiều mây	Không
7	Muộn	Tốt	Nắng	Có
8	Bình thường	Tốt	Nắng	Không
9	Sớm	Xấu	Nhiều mây	Có
10	Muộn	Tốt	Mưa	Có

Bằng việc lập bảng tần suất (frequency table) cho từng đặc trưng theo mục tiêu, có thể tính được likelihood P(X|y).

Giờ dậy (x1)

	Muộn	Không muộn	P(x1\|Muộn)	P(x1\|Không muộn)
Sớm	1	3	1/5	3/5
Bình thường	1	2	1/5	2/5
Muộn	3	0	3/5	0/5

Sức khoẻ (x2)

	Muộn	Không muộn	P(x2\|Muộn)	P(x2\|Không muộn)
Tốt	3	2	3/5	2/5
Xấu	2	3	2/5	3/5

Thời tiết (x3)

	Muộn	Không muộn	P(x3\|Muộn)	P(x3\|Không muộn)
Nắng	3	2	3/5	2/5
Nhiều mây	1	2	1/5	2/5
Mưa	1	1	1/5	1/5

Giả sử, để dự đoán cho một ngày X=(Muộn, Xấu, Mưa), cần tính:

P(Muộn|X) ∝ P(Muộn|Muộn) * P(Xấu|Muộn) * P(Mưa|Muộn) * P(Muộn) = (3/5) * (2/5) * (1/5) * (5/10) = 0.024

P(Không muộn|X) ∝ P(Muộn|Không muộn) * P(Xấu|Không muộn) * P(Mưa|Không muộn) * P(Không muộn) = (0/5) * (3/5) * (1/5) * (5/10) = 0

=> y = argmax{ P(X|y)P(y) } = Muộn.

Vì vậy, nếu anh chàng nhân viên thấy báo thức reo rồi mà còn cố ngủ thêm 15 phút, lúc dậy thân thể uể oải, nhìn ra ngoài trời thấy đang mưa, thì khả năng rất cao là hôm nay sẽ bị trừ lương.

4. Kết luận

Mô hình Naive Bayes là mô hình phân lớp đơn giản dễ cài đặt, có tốc độ xử lý nhanh. Tuy nhiên có nhược điểm lớn là yêu cầu các đặc trưng đầu vào phải độc lập, mà điều này khó xảy ra trong thực tế làm giảm chất lượng của mô hình. Thuật toán này thường được sử dụng trong phân tích sắc thái, lọc thư rác, recommendation systems, ...