Machine Learning Algorithms From Scratch With Ruby: Linear Regression

Bài đăng này đã không được cập nhật trong 2 năm

The best way for programmer to understand the machine learning algorithms is implement them from scratch. So, in this post I am going write an algorithm using my favorite language Ruby and Python and I'll write Linear Regression algorthm.

Why is Linear Regression?

Linear regression is a very simple algorithm but it is one of the most well known and well understood algorithms in statistics and machine learning. And it has very simple formular:

y = B0 + x * B1

where:

y: is the predicted output(label) for that set of input(feature) values.
x: is a specific set of input(feature) values.
B0: is the specific values used for the coeffcients.
B1: is the specific values used for the coeffcients.

And we are going to write an algorithm to find the best B0 and B1 from the given set of traning data x, y.

Note: In order for me to easy understand the formular, I define, y as label, x as feature, B0 as error, and B1 as multiplier. So we got label = feature * multiplier + error.

Simple Linear Regression

Simple linear regression use statistics to estimate the coeffcients. it calculate statistical properties from the data such as means, standard deviations, correlations and covariance. And we have the equation:

Let's convert the equation into ruby code.


class SimpleLinearRegression
  attr_accessor :multiplier, :error

  def initialize(multiplier = 0.0, error = 0.0)
    self.multiplier = multiplier
    self.error = error
  end

  def fit(features, labels)
    calculate_multiplier_and_error(features, labels)
    puts "Multiplier: #{self.multiplier}"
    puts "Error: #{self.error}"
  end

  def predict(feature)
    return self.multiplier * feature + self.error
  end

  private

  def calculate_multiplier_and_error(features, labels)
    mean_features = mean(features)
    mean_labels = mean(labels)

    dividend = 0.0
    divisor = 0.0
    (0...labels.size).each do |index|
      # dividend = sum((features[i] -mean_features) * (labels[i] -mean_labels))
      dividend += (features[index] - mean_features) * (labels[index] - mean_labels)
      # divisor = sum((features[i] -mean_features) ** (features[i] -mean_features))
      divisor += (features[index] - mean_features) ** 2
    end
    # multiplier = dividend / divisor
    self.multiplier = dividend / divisor
    # error = mean_labels - self.multiplier * mean_features
    self.error = mean_labels - self.multiplier * mean_features
  end

  def mean(arr_data)
    arr_data.reduce(:+) / arr_data.size.to_f
  end
end

It's time to train and predect data using our implemented algorithm.

# load sample data
features = [1,2,4,3,5]
labels = [1,3,3,2,5]
puts "SimpleLinearRegression testing"
puts "Features: #{features}"
puts "Labels: #{labels}"
puts "-" * 50
puts "Training"
# init model
model = SimpleLinearRegression.new()
# train the model
model.fit(features, labels)
puts "-" * 50
puts "Prediction"
puts "Predict the known data"
# predict label by the given feature
features.each_with_index do |n, index|
  puts "x= #{n}, pred y: #{model.predict(n)}, actual y: #{labels[index]}"
end
puts "Predict the unknown data"
pred_label = model.predict(10)
puts "the predict of given feature 10 is: #{pred_label}"

And the the result:

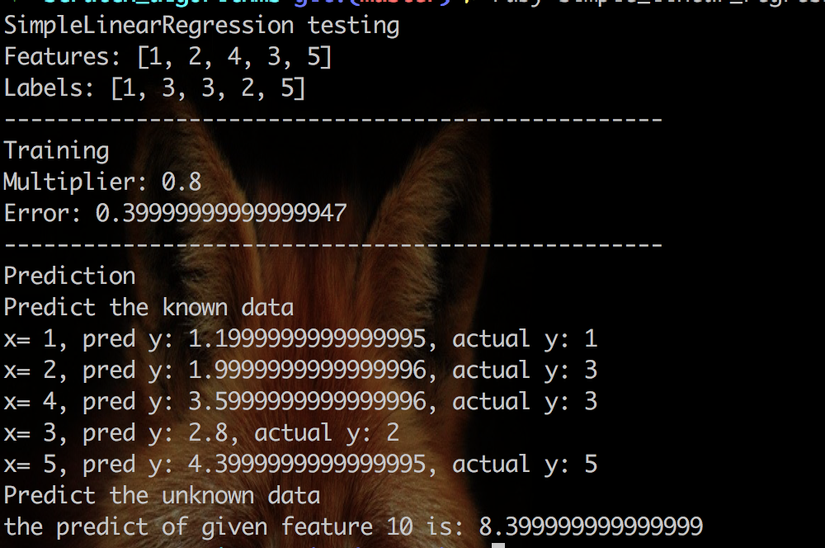
It's working. Awesome.

Gradient Descent Linear Regression

Gradient Descent is a process of optimizing the values of the coeffcients by iteratively minimizing the error of the model on your training data and it works by starting with zero values for each coeffcient. A learning rate is used as a scale factor and the coeffcients are updated in the direction towards minimizing the error. The process is repeated until a minimum sum squared error is achieved or no further improvement is possible. And we can sum them up as the equation belove:

Let's convert the equation into ruby code.

class GradientDescentLinearRegression
  attr_accessor :multiplier, :error, :alpha, :epochs

  def initialize(alpha = 0.01, epochs = 10, multiplier = 0.0, error = 0.0)
    self.alpha = alpha
    self.epochs = epochs
    self.multiplier = multiplier
    self.error = error
  end

  def fit(features, labels)
    update_weights(features, labels)
    puts "alpha: #{self.alpha}"
    puts "epochs: #{self.epochs}"
    puts "multiplier: #{self.multiplier}"
    puts "error: #{self.error}"
  end

  def predict(feature)
    return self.multiplier * feature + self.error
  end

  private

  def update_weights(features, labels)
    self.epochs.times do
      (0...labels.size).each do |index|
        # calculate the prediction
        predicted = self.multiplier * features[index] + self.error

        # calculate the error
        err = predicted - labels[index]

        # update multiplier and error
        self.error =  self.error - alpha * err
        self.multiplier = self.multiplier - alpha * err * features[index]
      end
    end
  end
end

Let's test our implemented code.


# load sample data
features = [1,2,4,3,5]
labels = [1,3,3,2,5]
puts "GradientDescentLinearRegression testing"
puts "Features: #{features}"
puts "Labels: #{labels}"
puts "-" * 50
puts "Training"
# init model
model = GradientDescentLinearRegression.new()
# train the model
model.fit(features, labels)
# predict label by the given feature
puts "Predict the known data"
features.each_with_index do |n, index|
  puts "x= #{n}, pred y: #{model.predict(n)}, actual y: #{labels[index]}"
end
puts "Predict the unknown data"
pred_label = model.predict(10)
puts "-" * 50
puts "Prediction"
puts "the predict of given feature 10 is: #{pred_label}"

Here the result:

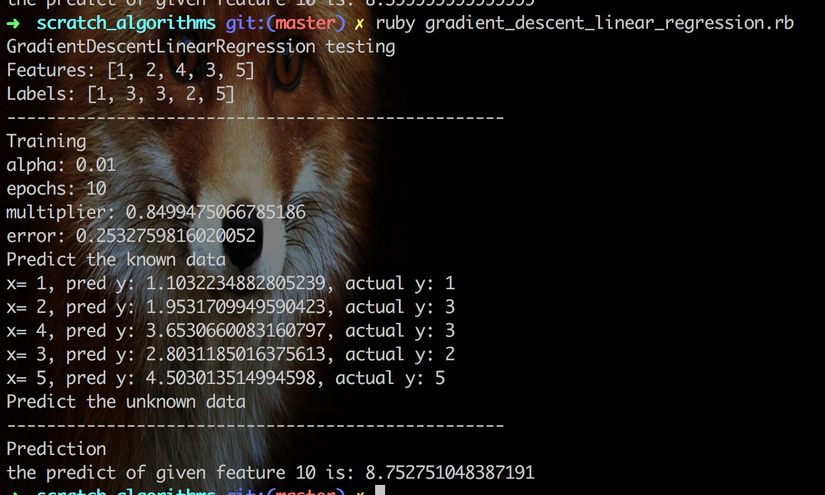
Look great.

Resources

Final Word

In this post, we talk about how to implement linear regression algorithms step-by-step. You have learned:

How to calculate the coeffcients(multiplier, error) for a linear regression model from the training data
How to make predictions using your learned model

You now know how to implement it from scratch. However, this implementation is used for helping you understand how linear regression algorithm work only. If you want to use linear algorithm for real work problems, you better use implementation from some library like sk-learn, .. etc instead because it is well written and well tested.

Why is Linear Regression?

Simple Linear Regression

Gradient Descent Linear Regression

Resources

Final Word

Mục lục