Câu hỏi được đặt ra

Sau một thời gian đi hóng phỏng vấn của các tay to trong team thì một câu hỏi hay được đặt ra để phân biệt giữa người hiểu lơ mơ và người hiểu không lơ mơ lắm chính là câu hỏi trên đề bài:

Phân biệt sự khác nhau giữa hồi quy tuyến tính và phân lớp tuyến tính?

Vậy thì bài viết này sẽ giải thích cụ thể sự khác nhau đó nhé, kèm tất cả những gì liên quan đến cả 2 mô hình trên. Nếu có lỡ múa rìu qua mắt thợ, xin mọi người hãy lượng thứ, và comment nhẹ nhàng chúng ta trao đổi dưới comment section nhé :'3

Sự khác nhau về mặt tính chất bài toán

Như tên gọi thì đây là 2 bài toán khác hẳn nhau:

• Hồi quy tuyến tính lấy vào các đặc trưng và đưa ra một số thực trong dải $(-\infty,+\infty)$

Ví dụ: bài toán định giá nhà đất (giá trị không dương ám chỉ lỗ/không đáng mua), bài toán định giá cổ phiếu (giá trị âm gợi ý nên dùng một lựa chọn phái sinh thích hợp), v.v.

• Phân lớp tuyến tính lấy vào các đặc trưng và đưa ra quyết định kết quả đầu vào thuộc về một lớp nào đó. Thường bài toán này sẽ đưa ra một/các số là các xác suất đầu vào rơi vào một lớp nào đó. Trong bài toán có $m$ lớp, thuật toán này sẽ trả lại $m$ số trong khoảng $(0,1)$, cố tổng bằng $1$, tạo thành một phân bố rời rạc không trùng.

Ví dụ: phân loại chó mèo, phân loại trong ảnh có xúc xích hay không (phân lớp nhị phân), nhận biết ảnh chữ số (phân lớp 10 loại: các chữ số từ 0 đến 9), v.v.

Sự khác nhau về công thức toán học

Như đã nói ở trên thì 2 bài toán này chỉ giống nhau ở điểm "tuyến tính." Tuyến tính ở đây nói về tổ hợp tuyến tính: đó là một kết hợp đó mỗi phần tử chỉ ở bậc nhất (không có bình phương (bậc 2), lập phương (bậc 3), hay các hàm phức tạp phi tuyến tính như $\log x$ hay exponential $e^x$). Trong trường hợp cơ bản nhất với hàm $f:\mathbb{R}^n\rightarrow\mathbb{R}^1$, khi chúng ta có các đặc trưng $\mathbf{x}=\begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix}\in\mathbb{R}^n$ phụ thuộc vào đầu vào, thì sau tổ hợp tuyến tính với trọng số $\mathbf{w}=\begin{bmatrix} w_1 \\ w_2 \\ \vdots \\ w_n \end{bmatrix}\in\mathbb{R}^n$, thì:

$$y=f(\mathbf{x})=w_1x_1+\dots+w_nx_n=\sum^n_{i=1}w_ix_i=\mathbf{w}^\top\mathbf{x},$$

trong đó $\mathbf{w}$ bao gồm các giá trị trọng số đã được tối ưu và cố định sau backpropagation.

Các lưu ý nho nhỏ:

• Trong các sách toán, trọng số có thể được đặt tên là $\mathbf{c}$, và vector biến (đặc trưng) có thể được đặt tên là $\mathbf{v}$.
• Các mạng tuyến tính thường có thêm số hạng bias $b$, biến công thức trên thành $y=\mathbf{w}^\top\mathbf{x}+b$. Số hạng này không thay đổi bất cứ lập luận nào trong bài này: bạn có thể coi đó là tham số/trọng số $w_0$ cho đặc trưng $x_0=1$ không phụ thuộc vào đầu vào.

Vậy sự khác nhau về công thức giữa giữa hồi quy tuyến tính và phân lớp tuyến tính là gì? Như đã nói ở phần trên, hồi quy tuyến tính đưa ra một kết quả thuộc $\mathbb{R}^n$, và công thức của nó chính là công thức đã viết ở trên. Còn với bài toán phân lớp nhị phân, đầu ra là một số xác suất đầu vào có thuộc vào lớp đó không - nói cách khác, một số thực trong khoảng $(0, 1)$. Công thức của bài toán này cũng rất đơn giản: làm giống hồi quy tuyến tính, rồi song ánh kết quả từ $(-\infty,+\infty)$ qua $(0,1)$ bằng hàm sigmoid:

$$\sigma(x)=\frac{e^{x}}{1+e^{x}}=\frac{1}{1+e^{-x}}.$$

Vậy, chúng ta lấy kết quả cuối cùng bằng công thức

$$y=\sigma(\mathbf{w}^\top\mathbf{x})=\frac{1}{1+e^{-\mathbf{w}^\top\mathbf{x}}},$$

và kết quả sẽ là xác suất cần tìm. Sigmoid ở đây là một ví dụ của hàm kích hoạt: hàm này sẽ dùng để biến đổi các đầu ra tuyến tính sang miền kết quả cần thiết, hoặc để thêm sự phi tuyến tính để tăng độ phức tạp của mô hình, v.v.

Fun fact/trivia: hàm sigmoid là một song ánh chứng minh kích cỡ không gian của $\mathbb{R}^n$ và $(0,1)$ là giống nhau, và cùng là $2^{\aleph_0}$ - với $\aleph_0$ là số số nguyên tồn tại (loại vô cực nhỏ nhất). Nếu giả thiết miền liên tục là đúng, thì con số đó sẽ tương đương với $\aleph_1$ (một loại vô cực to hơn).

Về toán thì ok hiểu sơ sơ rồi, nhưng mà vẫn không tưởng tượng được!

Công thức của $\mathbf{w}^\top\mathbf{x}(+b)$ là một đường thẳng trong không gian 2 chiều, và là 1 mặt phẳng (hyperplane) trong không gian nhiều chiều. Ở ví dụ 2 chiều $\mathbf{x}=(x_1, x_2)$, đường thẳng tương ứng với $\mathbf{w}=(3,2)$ nhìn như sau:

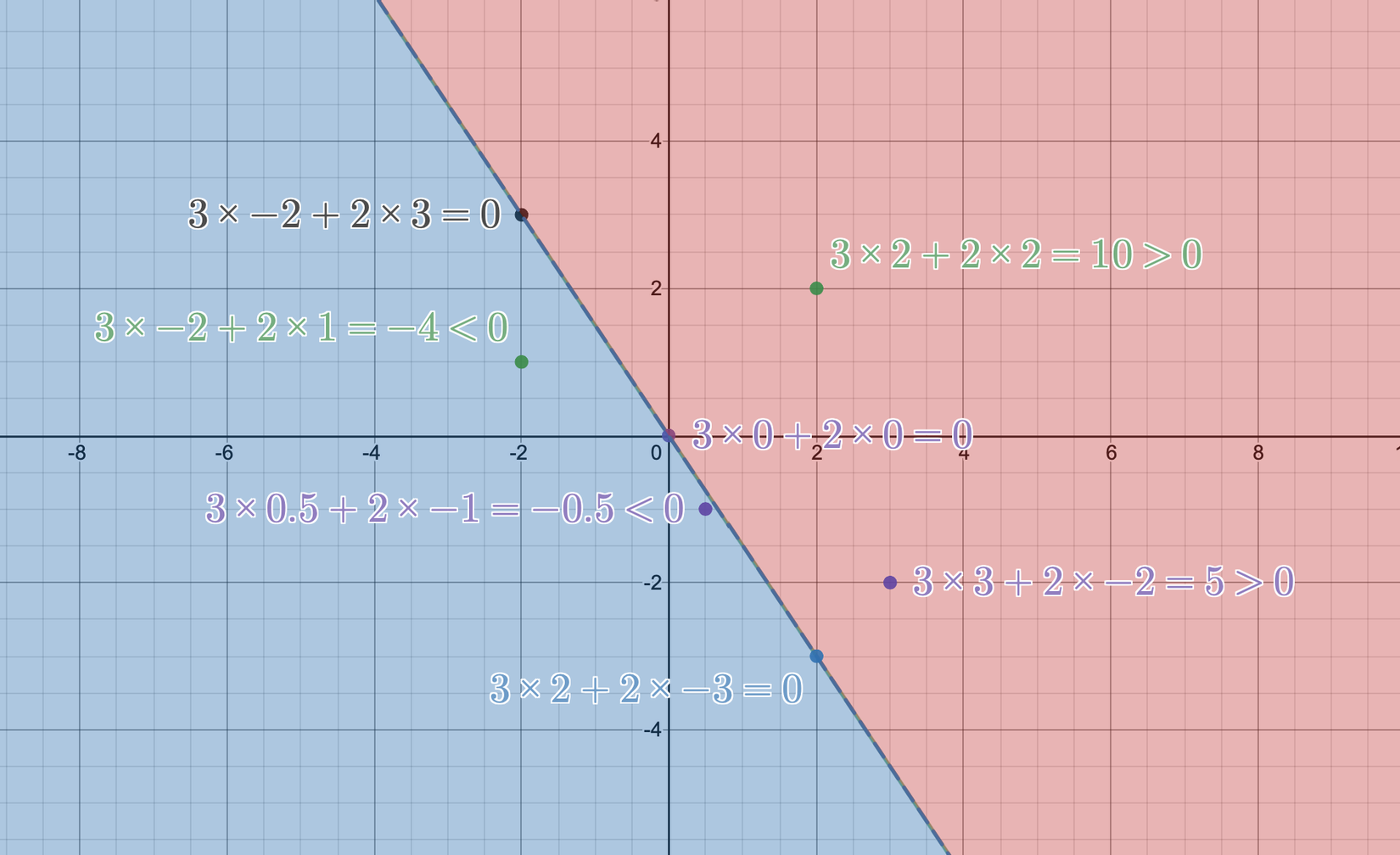
_{Mình xin lỗi vì màu chữ khó đọc, nhưng hãy trách Desmos - trang mình dùng để vẽ đồ thị. Nếu bạn có gợi ý trang nào tốt hơn, hãy comment giúp mình ở dưới nhé.}

Như chúng ta có thể thấy, đường thẳng đó chia mặt phẳng $\mathbb{R}^2$ thành 2 phần: các điểm $\mathbf{x}'$ nằm ở nửa màu đỏ sẽ có tính chất $\mathbf{w}^\top\mathbf{x}'>0$, các điểm nằm ở nửa màu xanh sẽ có tính chất $\mathbf{w}^\top\mathbf{x}'<0$, và các điểm nằm trên đường thẳng thì, như các bạn chắc cũng đoán được, $\mathbf{w}^\top\mathbf{x}'=0$.

Trong bài toán hồi quy tuyến tính, mặt phẳng 2 chiều như ảnh trên tương ứng với bài toán đặc trưng 1 chiều: chiều thứ 2 chính là giá trị tiên đoán đầu ra của mô hình:

• Với $x=2$, mô hình sẽ dự đoán $y=\frac{-3}{2}\times x = -3$.
• Với $x=-2$, mô hình sẽ dự đoán $y=\frac{-3}{2}\times x = 3$.
• Với $x=10$, mô hình sẽ dự đoán $y=\frac{-3}{2}\times x = -15$.

Trong bài toán phân lớp tuyến tính, mặt phẳng 2 chiều như ảnh trên tương ứng với bài toán đặc trưng 2 chiều: cả 2 chiều tương ứng với đặc trưng đưa vào, và việc nó rơi vào bên trái hay bên phải sẽ quyết định việc điểm đó được phân lớp đúng (bên màu đỏ) hay sai.

• Với $\mathbf{x}=(2,2)$, mô hình sẽ dự đoán "đúng": $\mathbf{w}^\top\mathbf{x}=10>0$.
• Với $\mathbf{x}=(3,-2)$, mô hình sẽ dự đoán "đúng": $\mathbf{w}^\top\mathbf{x}=5>0$.
• Với $\mathbf{x}=(-2,1)$, mô hình sẽ dự đoán "sai": $\mathbf{w}^\top\mathbf{x}=-4<0$.
• Với $\mathbf{x}=(0.5,-1)$, mô hình sẽ dự đoán "sai": $\mathbf{w}^\top\mathbf{x}=-0.5<0$.

Để ý kỹ hơn tí nữa, bạn sẽ nhận ra: sau khi được "kích hoạt," hàm sigmoid sẽ lớn hơn 0.5 với các giá trị đầu vào lớn hơn 0, và bé hơn 0.5 với các giá trị đầu vào nhỏ hơn 0.5. Giá trị càng lớn thì sau sigmoid càng gần 1, và càng bé thì sau sigmoid càng gần 0. Biểu đồ của hàm sigmoid nhìn như sau:

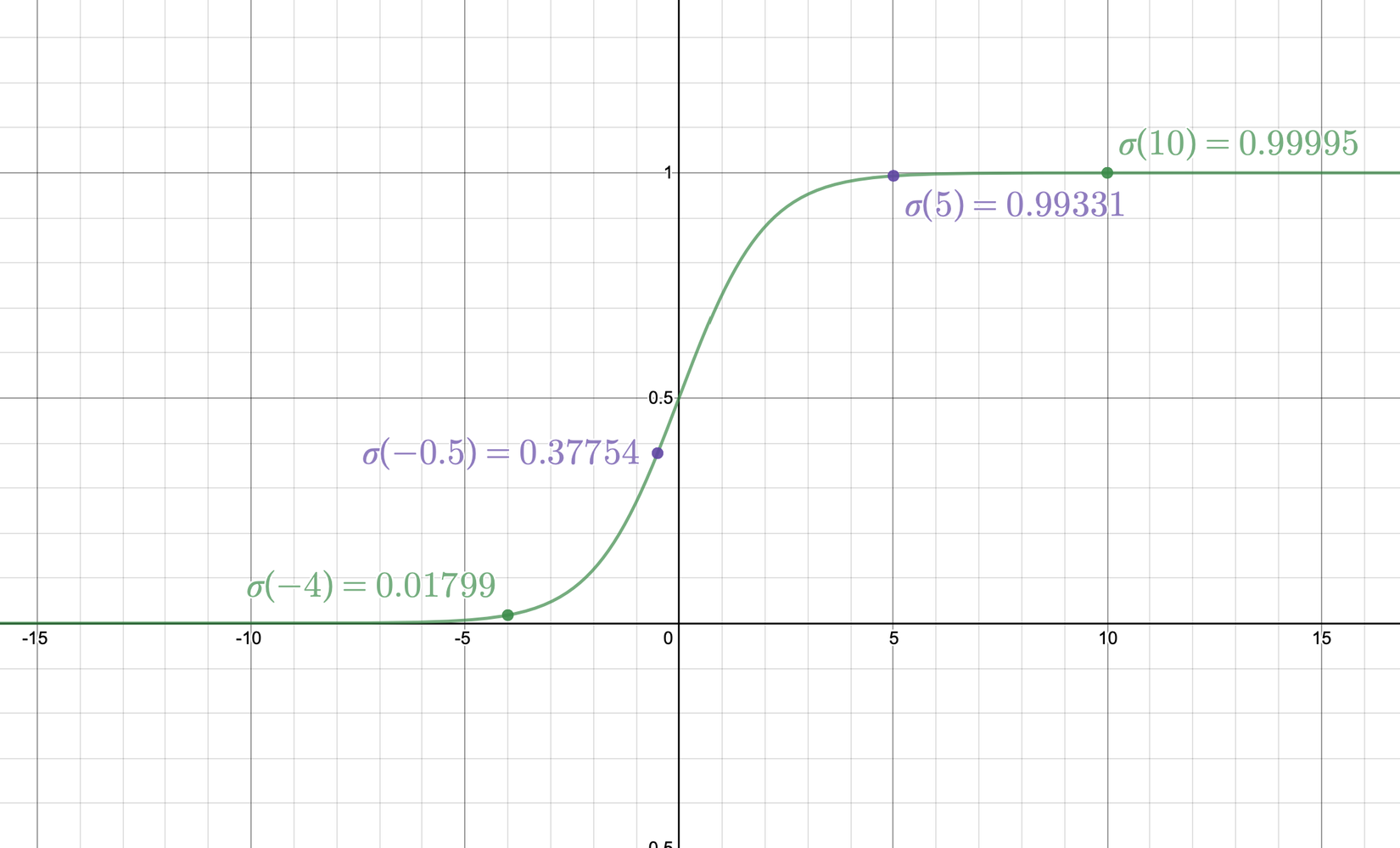
Vậy, giá trị sau khi qua phần tương tự như hồi quy tuyến tính cho ta một giá trị biểu trưng cho độ tự tin của mô hình về việc nhận xem đầu vào đó có thuộc lớp đó hay không: giá trị đó càng lớn thì xác suất càng gần 1, và nếu độ tự tin ở phía âm, thì xác suất càng gần 0, và nếu giá trị càng gần 0, thì xác suất càng gần 0.5, ám chỉ rằng mô hình không chắc chắn về kết quả:

• Với $\mathbf{w}^\top\mathbf{x}=10$, xác suất "đúng" là: $\sigma(\mathbf{w}^\top\mathbf{x})=0.99995$.
• Với $\mathbf{w}^\top\mathbf{x}=5$, xác suất "đúng" là: $\sigma(\mathbf{w}^\top\mathbf{x})=0.99331$.
• Với $\mathbf{w}^\top\mathbf{x}=-4$, xác suất "đúng" là: $\sigma(\mathbf{w}^\top\mathbf{x})=0.01799$.
• Với $\mathbf{w}^\top\mathbf{x}=-0.5$, xác suất "đúng" là: $\sigma(\mathbf{w}^\top\mathbf{x})=0.37754$.

Nhầm lẫn hay gặp phải: hàm sigmoid phân miền theo đồ thị.

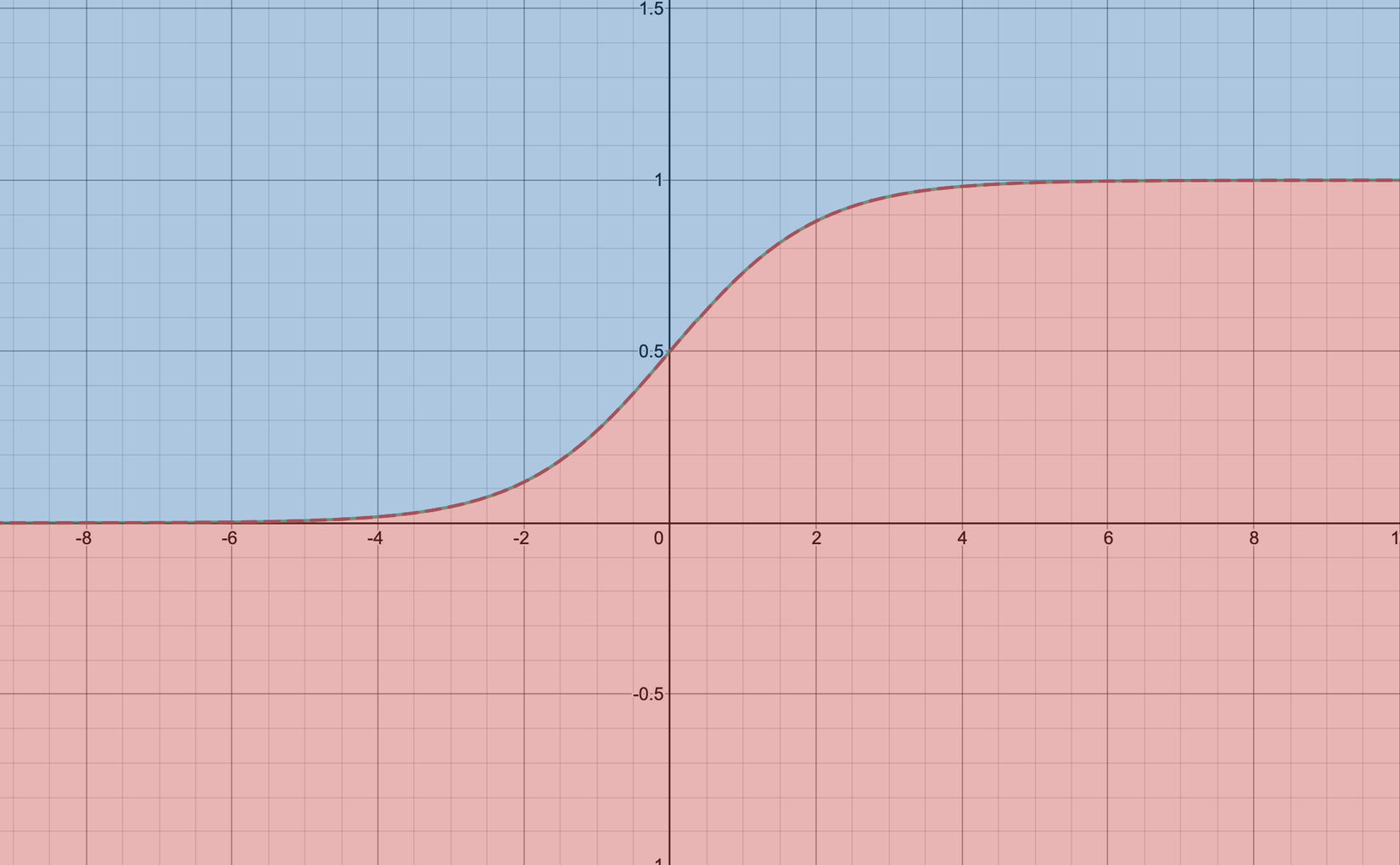
Như hình vẽ thì sigmoid cũng chia mặt phẳng ra thành 2 phần (như mọi hàm không tự cắt nhau khác). Tuy nhiên, cách hiểu đó là sai, vì 2 yếu tố sau:

• Hàm trên không tuyến tính. Thật dễ hiểu, khi nhìn vào, đường phân cách không phải là đường thẳng. Cụ thể hơn, thay vì dùng sigmoid để tạo ra giá trị xác suất, bạn đã sử dụng sigmoid để tạo ra sự phi tuyến tính trong hàm phân lớp. Công thức thực sự mà bạn đã sử dụng trong ví dụ sai này là $f(x_1,x_2)=\sigma(w_1x_1)+w_2x_2\overset{?}{=}0$.
• Giả sử như hàm sigmoid được dùng để thêm sự phi tuyến tính, phân lớp như trên cho các điểm ở mục đỏ có giá trị $f(\mathbf{x})>0$, và ngược lại ở vùng xanh; trong khi ở bài toán phân lớp tuyến tính khi sử dụng sigmoid để tạo ra xác suất, chúng ta phân lớp bằng cách so sánh giá trị kết quả với $0.5$.

Tất cả các thứ khác/Ngoài lề so sánh

Tại sao lại là sigmoid?

Ý tưởng của (các loại) hàm kích hoạt cho bài toán phân loại 2 lớp là, với các giá trị của độ tự tin (như đã định nghĩa ở phần trên) lớn hơn 0, hàm cần trả về kết quả là 1, và bé hơn 0 trả về kết quả là 0. Hoàn hảo nhất cho yêu cầu này là hàm bước Heaviside:

Tuy nhiên, hàm này có những nhược điểm không thể khắc phục: nó không tồn tại đạo hàm tại điểm 0, và đồng thời vô cùng không ổn định (unstable): đạo hàm của nó là $1$ khi $x>0$ và $-1$ khi $x<0$, và chỉ cần tốc độ học máy hơi cao quá chút thôi là kết quả đã không thể cứu chữa rồi. Vì vậy, lý do đơn giản nhất để chuyển qua sigmoid là vì hàm này có đạo hàm tại mọi nơi.

Ngoài ra, còn một lý do nữa quan trọng hơn liên quan đến xác suất thống kê. Nếu bạn tinh ý (hoặc biết trước), thì tất cả những gì mình đã mô tả về phân lớp tuyến tính cũng chính là định nghĩa của hồi quy logistic. Nếu xác suất đầu vào qua được mô hình phân lớp với kết quả "đúng" với xác suất $p$, thì tỷ lệ ăn/thua của đầu vào đó là $\frac{p}{1-p}$. Giả thiết của mô hình này là hàm $\log$ của tỷ lệ đó có quan hệ tuyến tính với các đặc trưng:

$$\log\frac{p}{1-p}=\mathbf{w}^\top\mathbf{x};$$

Vậy sau một hồi biến đổi bằng tay, bạn sẽ ra được

$$p=\frac{1}{1+e^{-\mathbf{w}^\top\mathbf{x}}},$$

chính là công thức cho sigmoid.

Các hàm phân lớp nhị phân khác

Tanh

Hàm $\tanh$ khác với sigmoid một cách cơ bản: đầu ra của $\tanh$ trong khoảng $(-1,1)$, nhưng lại vô cùng quen thuộc:

$$\tanh x = \frac{e^x-e^{-x}}{e^x+e^{-x}}=\frac{1-e^{-2x}}{1+e^{-2x}}=1-2\times\frac{1}{1+e^{-2x}}=1-2\sigma(2x).$$

Vậy ta có thể thấy $\tanh$ là một song ánh từ kết quả $(0,1)$ của sigmoid về $(-1,1)$.

Ngoài lề hơn nữa: Tại sao lại $(-1, 1)$? Tại vì với kết quả này ta có thể dễ dàng biểu diễn các hàm logic bằng perceptron! Với 2 giá trị logic $(x_1, x_2)$ ($>0$ cho True và $<0$ cho False), hàm AND có thể biểu diễn dưới dạng một mô hình tuyến tính với $\mathbf{w}=(1,1)$ và $b=-1$:

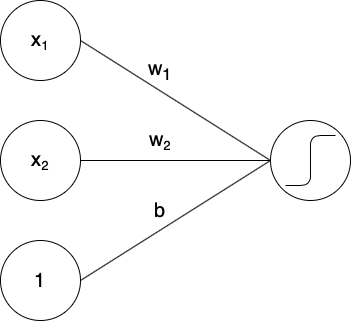
Vẽ bảng giá trị có thể sẽ chứng minh được ngay:

Tương tự các bạn có thể tự viết ra công thức cho các hàm logic khác (OR, XOR, NAND), cho biến thể kết hợp $>2$ giá trị, và cho trường hợp sử dụng sigmoid thay vì $\tanh$ nhé!

Hard sigmoid

Đây là một hàm ước lượng của sigmoid, với tính chất tuyến tính từng phần (piecewise-linear function), việc tính đạo hàm của nó rất nhanh.

Đa phần các module học máy đều đã định nghĩa hàm này: ví dụ như ở Theano, và ở Keras đều được đặt tên là hard_sigmoid:

$$\texttt{hard\_sigmoid}(x)=\begin{cases} 0 & \text{if }x<-2.5,\\ 1 & \text{if }x>-2.5,\\ 0.2x+0.5 & \text{otherwise}.\\ \end{cases}$$

Ngoài ra, Theano còn có ultra_fast_sigmoid: cũng là một hàm tuyến tính từng phần, nhưng sát hơn hàm sigmoid thật rất nhiều, như đã được biểu diễn trên biểu đồ trên.

Hàm mất mát

Một điểm khác nhau nữa của 2 bài toán trên là hàm mất mát: với mỗi tính chất một bài toán, một hàm mất mát khác nhau được sử dụng một cách phù hợp.

Bài toán hồi quy tuyến tính

Trong bài toán hồi quy tuyến tính, do tính chất đầu ra là một số thực, có 2 hàm mất mát thường được sử dụng:

MSE - Mean Squared Error ($l_2$ loss)

$$l(\mathbf{y},\hat{\mathbf{y}})=\frac{1}{n}\Vert\mathbf{y}-\hat{\mathbf{y}}\Vert_2^2=\frac{1}{n}\sum_{i=1}^n(y_i-\hat{y}_i)^2$$

Hàm mất mát này được sử dụng gần như mọi lúc mọi nơi vì nó đã được nghiên cứu đến chết rồi. Ưu điểm thì vô cùng: hàm đơn giản, đạo hàm tồn tại và dễ tính, và có mối quan hệ mật thiết với giả nghịch đảo: kết quả tối ưu của bài toán này với trường hợp perceptron đơn giản đang được đặt ra $\mathbf{Y}=f(\mathbf{X})=\mathbf{XW}$ là:

$$\mathbf{W}=\mathbf{X}^\dagger\mathbf{Y}=(\mathbf{X}^\top\mathbf{X})^{-1}\mathbf{X}^\top\mathbf{Y}.$$

Chứng minh nhanh: ta có

$$\mathbf{XW}=\mathbf{Y}\Rightarrow\mathbf{X}^\top\mathbf{XW}=\mathbf{X}^\top\mathbf{Y}\Rightarrow\mathbf{W}=(\mathbf{X}^\top\mathbf{X})^{-1}\mathbf{X}^\top\mathbf{Y}.$$

Hệ quả của chứng minh trên là chúng ta không phải backprop gì cho mệt mỏi cả, một phép toán ra luôn kết quả tối ưu rồi! Tuy nhiên với các bài toán phức tạp hơn như Multi-Layer Perceptron hay các mạng có (nhiều) yếu tố phi tuyến tính thì các bạn vẫn phải sử dụng backprop như thường lệ.

MAE - Mean Absolute Error ($l_1$ loss)

$$l(\mathbf{y},\hat{\mathbf{y}})=\frac{1}{n}\Vert\mathbf{y}-\hat{\mathbf{y}}\Vert_1=\frac{1}{n}\sum_{i=1}^n\vert y_i-\hat{y}_i\vert$$

Tương tự với MSE, hàm mất mát này sẽ càng ngày càng giảm (về gần 0) khi $y_i$ càng ngày càng tiến tới $\hat{y}_i$. Tuy nhiên, có thể thấy rằng hàm này không tồn tại đạo hàm tại mọi nơi (cụ thể là $l'(0)$ không tồn tại). Vậy tại sao hàm này vẫn được dùng trong thực tế?

Lý do là sử dụng MAE làm cho mô hình tăng độ thưa thớt (sparsity). Như chúng ta đã biết, mô hình học máy có một vấn đề muôn thuở là overfitting - vì vậy, chúng ta có nhiều cách làm giảm độ phức tạp của một mô hình đi, trong đó có một cách là làm tăng độ thưa thớt của các tham số. Sau đó, chúng ta có thể sử dụng cắt tỉa (pruning) và giảm số tham số một cách đáng kể (gần 90%!) mà vẫn giữ nguyên (thậm chí còn tăng!) độ chính xác của mô hình.

_{Về việc cắt tỉa, các bạn có thể tham khảo phiên bản rút gọn tại đây, một bài viết khá hay của đệ mình Phạm Hữu Quang (chỉ cần đọc mục Pruning thôi nhé!); hoặc phiên bản dài dằng dặc tại đây, một bài viết từ sếp của mình Phạm Văn Toàn.}

Lý do mà MAE làm tăng độ thưa thớt của mô hình? Một cách đơn giản dễ hiểu nhất là hãy nhìn vào biểu đồ sau:

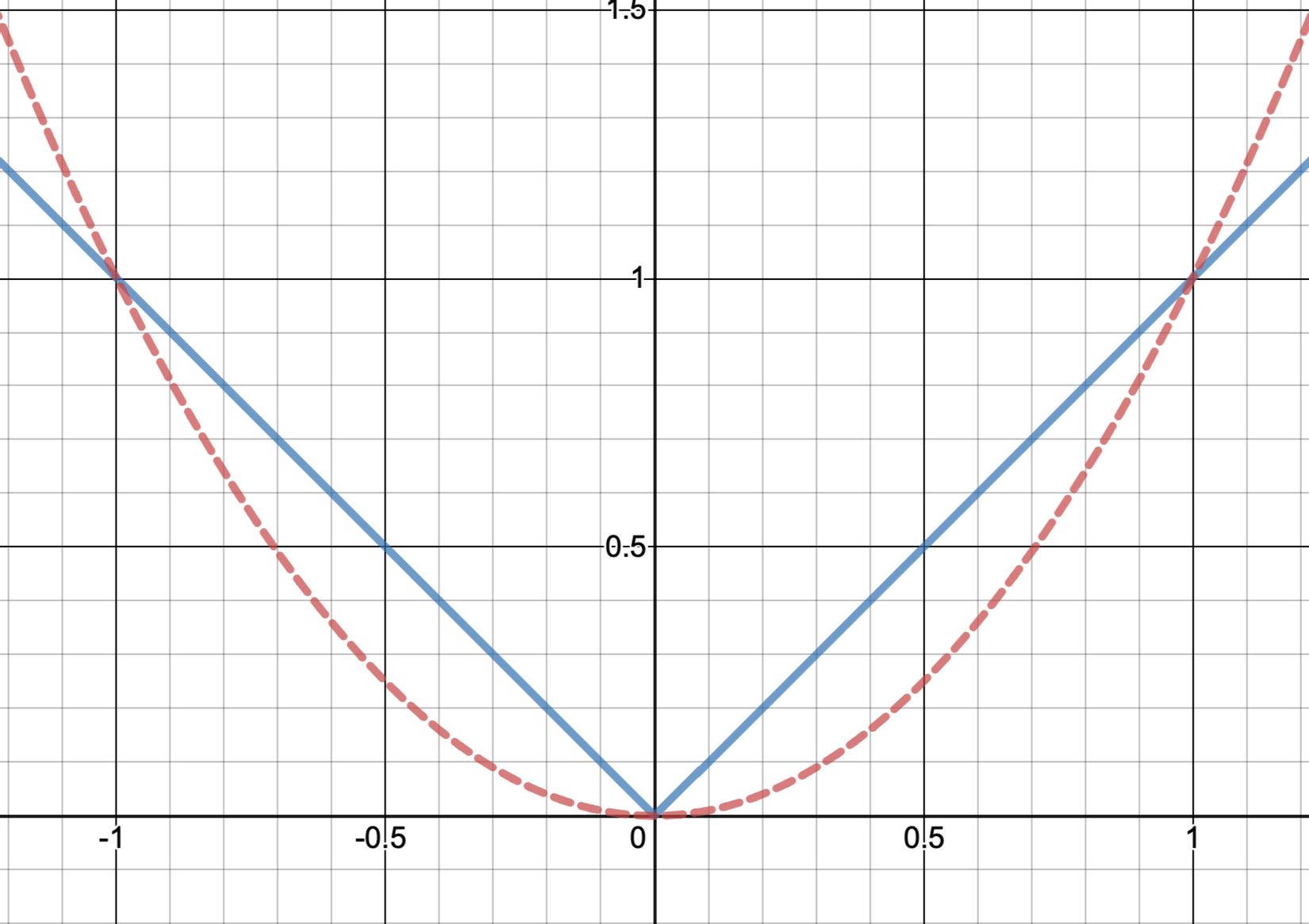
_{Đường xanh liền là MAE, đường đỏ đứt là MSE.}

Thường thì hàm mất mát sẽ xuống tới rất thấp dưới 1 (tầm $10^{-4}$ đến $10^{-6}$). Chúng ta có thể thấy, trong khoảng đó, cùng để giảm một tham số xuống cùng một giá trị thì loss của MSE giảm có 1 tí tẹo, trong khi loss của MAE giảm đi gấp nhiều lần. Vì vậy, thực tế thì không phải là MAE làm tăng độ thưa thớt, mà là MSE làm giảm độ thưa thớt.

Bài viết này cũng cho biết rằng MSE sẽ ra kết quả kém hơn MAE nếu như tập dữ liệu của chúng ta có nhiều kết quả nhiễu/đánh kết quả sai. Ngoài ra, nếu MAE được sử dụng trong một phần nhỏ của hàm mất mát, nhiều khi MSE được sử dụng thay thế tạm thời (surrogate loss/proxy norm), với hi vọng rằng nếu MSE giảm thì MAE cũng giảm. Đương nhiên là kết quả về độ thưa thớt (hoặc các tính chất khác) sẽ không thể tốt bằng MAE, tuy nhiên nếu hàm mất mát quá phức tạp thì nhiều lúc chúng ta phải đánh đổi bằng những ước lượng như vậy.

Bài toán phân lớp tuyến tính

Với bài toán phân lớp tuyến tính, ta có kết quả từ mô hình $y\in(0,1)$ sau sigmoid và kết quả thực $\hat{y}\in\{0,1\}$. Chúng ta cũng có thể sử dụng MAE/MSE để tối ưu, tuy nhiên các hàm mất mát đó khá là "ăn liền," và sẽ không tận dụng được tính chất bài toán để ra kết quả tốt nhất. Thay vì đó, chúng ta sẽ sử dụng hợp lý cực đại: từ xác suất đầu ra và xác suất thực, ta ra được công thức của hợp lý (từ giờ sẽ gọi là likelihood vì nghe tên tiếng Việt rất không hợp lý):

$$\mathcal{L}(\mathbf{y},\hat{\mathbf{y}})=y^{\hat{y}}(1-y)^{1-\hat{y}}.$$

Giải thích cơ bản ý nghĩa của giá trị trên: theo bài toán, chúng ta cần $y=\hat{y}$, và xét cả 2 trường hợp của giá trị đúng:

• Nếu $\hat{y}=1$, $\mathcal{L}=y$ cũng cần bằng 1 (giá trị tối đa),
• Nếu $\hat{y}=0$, $\mathcal{L}=1-y$ cũng cần bằng 1 (giá trị tối đa).

Cả 2 giá trị trên đều cần được tối đa, nên likelihood cũng cần được tối đa hoá. Giờ chúng ta lấy $\log$ của likelihood rồi đổi thành dấu âm, vì hàm $\log$ là hàm đồng biến và hàm âm (nhân $-1$) là hàm nghịch biến, nên sau khi áp dụng 2 biến đổi trên, chúng ta sẽ cần tối thiểu hoá công thức sau:

$$-\log\mathcal{L}(\mathbf{y},\hat{\mathbf{y}})=-\hat{y}\log{y}-(1-\hat{y})\log(1-{y}).$$

Công thức trên chính là hàm negative log-likelihood, và là hàm mất mát được sử dụng trong bài toán hồi quy logistic/phân lớp tuyến tính. Công thức trên cũng tương đương với việc tối thiểu hoá cross-entropy/phân kỳ Kullback-Leibler:

$$\begin{aligned} D_{KL}(\hat{y}\Vert y) &=\hat{y}\log\frac{\hat{y}}{y}-(1-\hat{y})\log\frac{1-\hat{y}}{1-y} \\ &=\hat{y}\log{\hat{y}}+(1-\hat{y})\log(1-\hat{y})-\hat{y}\log{y}-(1-\hat{y})\log(1-{y}) \\ &=O(\hat{y})-\log\mathcal{L}(\mathbf{y},\hat{\mathbf{y}}), \end{aligned}$$

với cách hiểu $y$ là xác suất của một phân bố Bernoulli. Vì phần đã được rút gọn lại thành $O(\hat{y})$ không phụ thuộc vào đầu vào của mô hình mà chỉ là một hằng số, nó không ảnh hưởng tới việc tối ưu hoá; đồng nghĩa với việc tối thiểu hoá hàm mất mát của phân kỳ K-L tương đương với việc tối thiểu hoá hàm mất mát của negative log-likelihood.

Phân lớp nhiều hơn 2 lớp

Có 2 cách để xử lý vấn đề này: one-versus-one và one-versus-rest. Trong trường hợp one-versus-one, chúng ta tạo ra nhiều mô hình để phân xem nó có thuộc một lớp bất kỳ hay không - cách này sẽ làm gia tăng lượng tham số một cách đáng kể. Với one-versus-rest, khi chúng ra giả thiết rằng một đầu vào có chính xác một lớp đầu ra, chúng ta có thể sử dụng softmax.

_{Nếu một đầu vào có thể có kết quả nhiều hơn một lớp, bạn cần quay lại sử dụng sigmoid như one-versus-one.}

• Đầu ra của mô hình/ground truth sẽ là one-hot encoding của kết quả thực: nếu kết quả là lớp $m$ trong $n$ lớp có thể xảy ra, thì ground truth sẽ là vector $n$ chiều toàn số 0, với chính xác 1 số 1 nằm ở vị trí $m$.
• Với đầu ra của mô hình $n$ lớp trước kích hoạt là $\mathbf{h}=\begin{bmatrix}h_1\\\vdots\\h_n\end{bmatrix}$, ta sử dụng softmax để kích hoạt như sau:

$$y_m=\text{softmax}(h_m;\mathbf{h})=\frac{e^{y_m}}{\sum^n_{i=1}e^{y_i}}.$$

• Khá là dễ nhận ra rằng hàm này cũng rất tương tự với sigmoid, đưa ra kết quả luôn dương có tổng bằng 1 (tạo thành một phân bố rời rạc), và nếu độ tự tin về kết quả một lớp lớn hơn một lớp khác thì xác suất sau kích hoạt của lớp đó sẽ lớn hơn lớp kia (hàm đồng biến). Vì vậy nên hàm này được gọi là softmax:
  • Kết quả đúng nhất sẽ ra xác suất rất gần 1 (giống như minh hoạ bằng biểu đồ của sigmoid), nên được sử dụng để thay thế cho hàm $\max$ (tương tự như sigmoid được sử dụng thay thế cho hàm bước Heaviside).
  • Hàm này liên tục và tồn tại đạo hàm tại mọi nơi (soft).
• Hàm mất mát của softmax là cross-entropy: tương tự với trường hợp của sigmoid (cũng từ MLE, chứng minh tương tự), với output của mô hình là $\mathbf{y}\in\mathbb{R}^n$ và kết quả thực (ground truth) $\hat{\mathbf{y}}\in\mathbf{R}^n$, hàm mất mát được định nghĩa là:

$$l(\mathbf{y}, \hat{\mathbf{y}})=-\hat{\mathbf{y}}\log{\mathbf{y}}=-\sum_{i=1}^n\hat{y}_i\log y_i.$$

Sự khác nhau giữa sigmoid và softmax 2 lớp

Đây cũng là một câu hỏi phỏng vấn nhiều người mất một chút thời gian để nghĩ: câu trả lời là chả khác nhau gì cả. Với softmax 2 lớp, ta có kêt quả của lớp 1 là:

$$p_1=\frac{e^{y_1}}{e^{y_1}+e^{y_2}}=\frac{1}{1+e^{-(y_1-y_2)}}.$$

Các bạn thấy quen thuộc chưa? Một đầu ra 2 số trước khi dùng softmax có hiệu tương ứng với đầu ra 1 số trước khi dùng sigmoid. Vậy, sigmoid sẽ cho cùng kết quả với softmax nhưng với it tham số hơn.

Kết bài

Cho dù toàn tự nhủ là mình hiểu gần hết và khá sâu các khái niệm cơ bản, tuy nhiên nhiều lúc mình chợt nhận ra là mình không hiểu gì hết cả! Vì vậy, mình viết ra bài này để giới thiệu các bạn là một phần thôi, mà là để mình tự củng cố kiến thức là nhiều. Cảm ơn các bạn đã đọc bài này, và hẹn gặp các bạn ở bài sau! Nếu bạn có câu hỏi nào muốn hỏi/mình giải thích, hãy comment dưới bài này, hoặc đặt câu hỏi trong Viblo nhé