Tấn công và phòng thủ bậc nhất cực mạnh cho các mô hình học máy
Bài đăng này đã không được cập nhật trong 4 năm
Update 2: Slides cho bài này đã được tạo để mình đi present tại ĐHBKHN, sau khi được approve sẽ update link sau.
Update 1: Bleeding edge của CleverHans đã lên từ 3.1.0 đến 4.0.0, và các tấn công cho PyTorch/JAX đã không còn là thử nghiệm. Code trong bài đã được update cho phiên bản mới nhất.
Giới thiệu
Lời mở đầu
Xin chào các bạn, sau nửa năm vắng bóng đi chơi CTF thì mình lại quay về với nghề kiếm cơm viết bài AI đây  Như title thì chắc các bạn cũng có thể thấy rằng đây là một phạm trù cũng khá liên quan, và sau khi đọc bài này thì có thể bạn sẽ làm được một vài bài CTF mới lạ (ví dụ, WGMY2019 có một challenge liên quan đến computer vision). Ngoài ra, mình có một bài Viblo CTF tương tự, các bạn có thể thử
Như title thì chắc các bạn cũng có thể thấy rằng đây là một phạm trù cũng khá liên quan, và sau khi đọc bài này thì có thể bạn sẽ làm được một vài bài CTF mới lạ (ví dụ, WGMY2019 có một challenge liên quan đến computer vision). Ngoài ra, mình có một bài Viblo CTF tương tự, các bạn có thể thử 
Hacking trong deep learning?
Có một quy tắc vàng trong lập trình là "never trust user input", hay tạm dịch là không bao giờ được tin rằng đầu vào của người dùng là an toàn. Tương tự trong deep learning cũng vậy, có thể bạn không thực thi code từ xa (RCE) được, nhưng bạn cũng có thể làm được vài thứ khá hay ho đấy.
Chắc bạn đã nghe thấy các hệ thống an ninh bằng cách nhận diện khuôn mặt rồi chứ? Nếu bây giờ mặt mình sửa mũi tí nhưng camera nhận ra mình là Joe Biden thì sao? Khỏi phải tràn vào Capitol Hill bằng vũ lực, mình có thể hiên ngang đi vào phóng tên lửa rồi (có lẽ vậy). Hoặc là thực tế hơn, hệ thống chống trộm của nhà bạn sẽ kêu lên nếu nhìn thấy có người đi qua. Tuy nhiên, dùng phương pháp in áo print-on-demand với các chi tiết đặc biệt, mình có thể né toàn bộ hệ thống đó và vào bê bồ bạn đi đấy.
Trong bài này thì mình sẽ không đề cập đến topic cụ thể trên đâu, mà chỉ trình bày về nhưng khái niệm tiền đề của các tấn công nói chung nên đừng hi vọng nhiều quá và bảo mình treo đầu dê bán thịt chó nhé 
Khái niệm cơ bản
Tấn công trong deep learning là sao?
Do mô hình học sâu có không gian đầu vào rất lớn và độ phức tạp lớn, nếu nó nhớ các dữ liệu đầu vào và khiến đường phân lớp (decision boundary) cố fit các điểm nhiễu, chúng ta có thể dễ dàng sửa đầu vào cho giống điểm data nhiễu kia để lừa mô hình. Đó là lý do tại sao các phương pháp data augmentation như thêm nhiễu/trộn đầu vào giúp cho mô hình không bị overfit vào training set. Chưa kể, đa số các mô hình hiện đại đều sử dụng batchnorm để có thể thành công train các model sâu, nhưng batchnorm lại khiến model dễ bị tấn công hơn rất nhiều.
Yêu cầu của tấn công
Lại một ví dụ nữa cho dễ hình dung nhé! Mình thì thích mèo, còn người yêu mình thì thích chó. Mình thì không thích chó, vì hồi bé có con nó tợp ngay gần háng ông anh họ mình. Mình thì muốn nuôi một con mèo, nhưng bồ mình thì có một hệ thống nhận diện request và tự động reject tất cả yêu cầu nuôi con gì mà không phải là chó. Thế mình bây giờ phải làm gì?
Đầu tiên, mình phải có ảnh con mèo mình muốn mua . Sau đó, chúng ta phải sửa ảnh đó tí tẹo sao cho cho mô hình nhìn hình nó phải đoán ra con chó. Cái ảnh đã sửa đó được gọi là adversarial example . Độ "tí tẹo" khác nhau giữa ảnh gốc và adversarial example có thể được tạo bằng cách thêm nhiễu hoặc các image deformity (như kiểu ảnh bị méo tí chỗ này lồi ra chỗ kia, cái này hơi khó dịch). Phổ biến nhất là thêm adversarial noise, nghĩa là nhiểu được thiết kế để tạo adversarial example; và độ khác nhau thường được tính bằng hoặc norm. Độ khác nhau đó sẽ bị giới hạn trên sao cho ảnh mới nhìn trông vẫn giống ảnh gốc. Ví dụ, trong trường hợp sử dụng , và độ chênh lệch tối đa là , chúng ta có yêu cầu như sau:
có chỗ nào cho nuôi nekomimi không nhỉ
Vậy thì phải làm gì đây?
Dạy mô hình sao cho nó không chỉ nhớ những gì nó đã thấy, mà phải biết để ý rằng ảnh con mèo chụp lệch sáng tí vẫn phải là con mèo. Cụ thể là, nếu đầu vào chỉ khác nhau chút đỉnh (theo một metric distance nào đó như đã mô tả ở trên), thì mô hình phải dự đoán ra cùng kết quả.
Bậc nhất (First-order)?
First-order ở đây là gì? Nghĩa là các phương pháp trong bài này hoạt động dựa trên gradient (bậc nhất) mà các model tạo ra trong quá trình feed-forward hoặc backwards. Điều này ám chỉ rằng các phương pháp này chỉ hoạt động trong điều kiện bạn có toàn bộ thông tin về mô hình, các trọng số, và đạo hàm bậc nhất của nó (white-box threat model). Nếu bạn muốn tìm phương pháp cho bài toán trường hợp hộp đen chỉ có kết quả phân lớp đầu ra, bạn có thể đọc bài viết về phương pháp HopSkipJumpAttack của mình.
Tấn công
Fast Gradient Sign Method
Được giới thiệu bởi dân chơi deep learning Ian Goodfellow vào năm 2015, FGSM là một phương pháp đơn giản nhưng hiệu quả để có thể sinh ra các adversarial example cho một mô hình học máy.

Như chúng ta đã biết, gradient của một trọng số theo hàm mất mát sẽ cho chúng ta biết trọng số phải thay đổi như thế nào để làm giảm hàm mất mát. Quá trình training một mô hình về cơ bản chỉ là sử dụng phương pháp trên, với tên gọi mỹ miều là gradient descent, để cập nhật các thông số của mô hình dần đến tối ưu (cực tiểu địa phương).
Tương tự như phương pháp trên, nhưng thay vì tối ưu trọng số của mô hình, chúng ta tối ưu chính ảnh đầu vào, và giữ nguyên (đóng băng) mô hình. Từ nhãn đúng, bắt đầu từ một ảnh con mèo, chúng ta sẽ tính gradient của ảnh đó theo hàm mất mát, và từ đó đi theo hướng đó để kết quả trả về của mô hình trở nên xa khỏi nhãn đúng — để ý đây là ngược lại với gradient descent, hay còn gọi là gradient ascent. Ngoài ra, thay vì chỉ thuần túy nhân gradient với một step size, chúng ta sử dụng công thức sau để chắc chắn ảnh không khác nhau quá theo độ đo :
trong đó là hàm mất mát. Có thể dễ thấy từ công thức trên thì
do kết quả hàm có tất cả các giá trị trong ma trận là , khiến adversarial example của chúng ta thỏa mãn yêu cầu về độ khác nhau tối đa.
Chú ý là những phương pháp này không chắc chắn sẽ tạo thành công một adversarial example cho một classification khác với ảnh gốc. Ngoài ra, tác giả Phạm Văn Toàn đã viết một bài về chủ đề này vô cùng chi tiết, các bạn có thể tham khảo để có ý tưởng và code PyTorch.
Basic Iteration Method
Đây là một cải tiến của FSGM của Kurakin et. al tại ICLR workshop 2017. Thay vì nhảy một nháy theo gradient với step size thì chúng ta nhảy nhiều nháy với step size . Tuy nhiên, đảm bảo về việc adversarial không khác ảnh gốc quá không còn đúng nữa, nên chúng ta phải clip lại cho vào đúng trong khoảng cho phép:
Công thức cụ thể của BIM như sau: bắt đầu với là ảnh gốc, mỗi iteration chúng ta update như sau:
Projected Gradient Descent
Projected Gradient Descent là một phương pháp tối ưu hóa cũng được sử dụng phổ biến, tương tự như SGD hay BFGS. Tại ICLR 2018, Madry et. al đã giới thiệu phương pháp này để tấn công mô hình, được mệnh danh là "the universal first-order adversary", phương pháp tấn công tối ưu sử dụng dữ liệu đạo hàm bậc nhất của mô hình. Ngoài ra, paper đó còn giới thiệu phương pháp training mô hình chống adversarial example — phần này sẽ được đề cập ở phần dưới.
Phương pháp này tương tự với BIM, tuy nhiên bao gồm vài điểm khác nhau:
-
PGD bắt đầu không tại ảnh gốc, mà là tại một điểm ngẫu nhiên trong khoảng cho phép xung quanh ảnh gốc.
Lý do là với mô hình đã train hết cỡ với các ảnh trong tập train, gradient của hàm mất mát với các ảnh đó có thể tiến tới 0, và gradient descent/ascent sẽ không thay đổi gì cả.
-
PGD thêm hỗ trợ cho (và các metric distances khác) thay vì chỉ , bằng cách tổng quát hóa hàm bằng hàm chiếu (projection) . Công thức mới sẽ như sau:
Công thức trên hơi khác với trong paper do đã được sửa để thống nhất với các công thức từ các paper/tấn công trước.
Trong trường hợp , hàm chiếu chính là hàm . Trong trường hợp , bề mặt cần được chiếu xuống là một khối cầu đa chiều (hypersphere) có bán kính là xung quanh ảnh gốc, và hàm chiếu được tính như sau:
-
(Bonus) Thí nghiệm về PGD trong paper thỉnh thoảng lại khởi động lại tại một điểm ngẫu nhiên như định nghĩa ở trên.
Khởi động lại quá trình tấn công tại các điểm khác nhau giúp khám phá toàn bộ loss landscape xung quanh ảnh gốc và phân tích độ hiệu quả của thuật toán.
PyTorch code (hay tương tự với TensorFlow) cho PGD cũng khá đơn giản, đặc biệt với sự giúp đỡ của các adversarial toolbox như CleverHans của CleverHans Lab, Foolbox của Bethge Lab, hay Adversarial Robustness Toolbox của IBM. Sau đây là code sử dụng CleverHans cho PGD — chú ý rằng CleverHans support cho PyTorch hiện đang chỉ ở bản bleeding edge (ver. 4.0.0) nhưng không tồn tại trong phiên bản trên pip (ver 3.0.1), nên bạn phải compile lại code trên GitHub của project:
pip install git+https://github.com/tensorflow/cleverhans.git#egg=cleverhans
Rồi từ đó chỉ cần import và chạy:
from cleverhans.torch.attacks.projected_gradient_descent import projected_gradient_descent as PGD
# optional, only for linf norm or something else
import numpy as np
adversary = PGD(
model, original_data, eps=eps, eps_iter=eps_iter, nb_iter=nb_iter,
norm=np.inf, clip_min=-1., clip_max=1.
)
Trong đó
adversary: adversarial example đầu ramodel: mô hình bị tấn côngoriginal_data: ảnh gốc cần bị chỉnh sửaeps: khoảng cách tối đa giữa ảnh gốc và adversarial exampleeps_iter: độ dài bước nhảy mỗi iterationnb_iter: số iteration chạy FGSM (update adversarial example theo gradient) trong cả quá trình PGDnorm: metric distance giữa ảnh gốc và adversarial example, hiện chỉ supportnp.infcho hoặc2cho .
Phòng thủ
PGD-Adversarial Training
Khái niệm về adversarial training đã được giới thiệu từ paper FGSM, tuy nhiên tấn công đó không quá mạnh để đủ hiệu quả. Trong paper về PGD, tác giả đã giới thiệu adversarial training với tấn công PGD cho hiệu quả, và có đưa ra một vài kết luận về ảnh hưởng của hyperparameters.
Việc train mô hình theo phương pháp này khá đơn giản như sau: thay vì train đầu vào và ground truth , chúng ta thay đầu vào với PGD adversarial example được tạo ra để tấn công phiên bản trọng số mô hình hiện tại.
Code PyTorch khá đơn giản:
# define some model beforehand
model = model.to(device)
criterion = torch.nn.CrossEntropyLoss()
# based on robust overfitting src code
optimizer = torch.optim.SGD(model.parameters(), lr=lr, momentum=0.9, weight_decay=5e-4)
# define the rest of the training parameters
eps, eps_iter, nb_iter = ...
for epoch in range(epochs):
trainloader = torch.utils.data.DataLoader(
trainset, batch_size=batch_size, shuffle=True, num_workers=cpu_count()
)
for minibatch, (vanilla, labels) in enumerate(trainloader):
vanilla = vanilla.to(device)
labels = labels.to(device)
# generate adversary
model.eval()
adversary = PGD(
model, vanilla, eps=eps, eps_iter=eps_iter, nb_iter=nb_iter,
norm=np.inf, clip_min=-1., clip_max=1.
)
model.train()
# zero the gradient beforehand
optimizer.zero_grad()
# adversarial output
adversary_output = model(adversary)
loss = criterion(adversary_output, labels)
# update weights
loss.backward()
optimizer.step()
Tuy nhiên, chú ý rằng train một mô hình PGD-AT theo như paper sẽ mất thời gian gấp 10 lần so với train bình thường. Cũng dễ hiểu, vì mỗi một training epoch chúng ta phải sinh ra các adversarial example mới, và tốc độ hội tụ cũng sẽ chậm hơn do data thay đổi theo mô hình (cụ thể hơn là decision boundary), và cả 2 phải cùng kéo nhau hội tụ (chứ không phải 1 cái đã biết điểm tối ưu và kéo cái còn lại về đó). Trong thực tế, lúc mình train chỉ mất có gấp 3 lần thôi nên vô tư đi.
TRADES
Là người chiến thắng cuộc thi NeurIPS 2018 Adversarial Vision Challenge (cách giải nhì tới 11.41%!), Zhang et. al giới thiệu một phương pháp training mô hình dùng để tối ưu tradeoff giữa tối ưu standard accuracy — xác suất dự đoán đúng class của đầu vào tự nhiên; và robust accuracy — xác suất dự đoán đúng class của các adversarial example. Trong paper có rất nhiều toán phức tạp chúng minh một tight bound cho robust accuracy cho các hàm mất mát phổ biến. Tuy nhiên, tất cả những gì bạn cần rút ra là phương pháp này được train với objective như sau:
trong đó là hàm mất mát như cross-entropy, giống như trong các định nghĩa của các phương pháp tấn công ở trên; và có nhiệm vụ của một regularizing coefficient giúp tradeoff giữa tối ưu xác suất dự đoán đúng (số hạng đầu) và xác suất tấn công thất bại (số hạng sau).
Sự khác nhau của phương pháp này với các phương pháp trên là việc train các adversarial example được thực hiện với soft label thay vì true label , từ đó adversarial training không phải dần kéo decision boundary về đúng với data, mà thay vì đó đang ép cho decision boundary được smooth (mượt) — với các đầu vào gần giống nhau thì kết quả đầu ra cũng phải gần giống nhau.
Tuy nhiên, phương pháp này có một điểm yếu trong thí nghiệm không bị phát hiện ra cho đến paper sau:
Robust Overfitting
Một kết quả khá bất ngờ đến từ Rice et. al, được publish tại ICLR 2020. Trong đó, tác giả cho thấy rằng TRADES thành công do họ chọn best checkpoint trong code của họ (và việc đó tương tự với việc sử dụng early stopping), và nếu train TRADES gấp đôi đến chết thì robust accuracy sau một điểm sẽ càng ngày càng giảm:

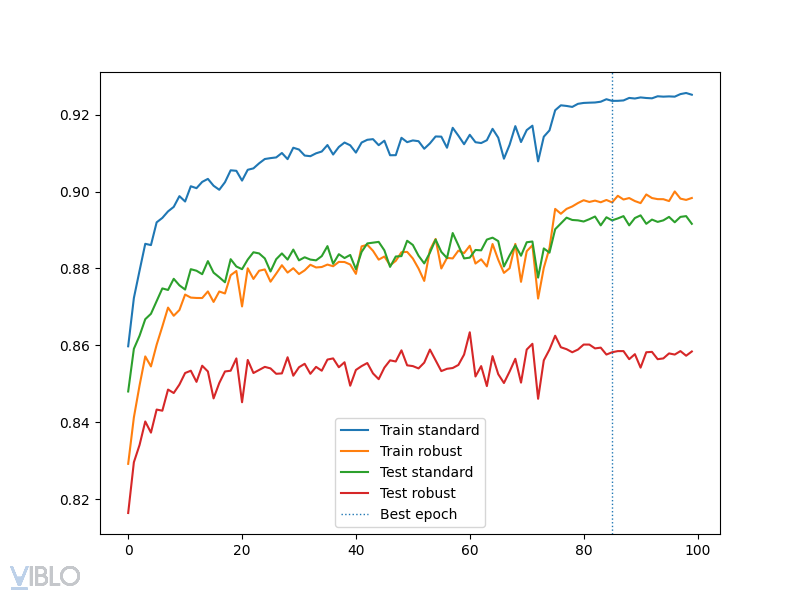
Trong đó, cụ thể các chỗ accuracy nhảy lên/xuống đột ngột là khi thay đổi learning rate. Trong đó, kết luận của paper là sau lần giảm learning rate đầu tiên, mô hình sẽ tốt lên rất nhanh lúc đầu, rồi sau đó trong khi model fit càng ngày càng tốt lên với training set, robust accuracy cho test set lại càng ngày càng tệ dần. Tác giả sau đó gợi ý chúng ta có thể chọn early stop mô hình bằng một tập validation riêng, chỉ cần tầm 1000 examples là được. Với early stopping, tác giả cho biết PGD-AT có kết quả còn cao hơn TRADES.
Code thì bạn chỉ cần sửa tí tẹo từ code PGD-AT ở trên nhé  Và đây là plot mình tự train để kiểm chứng trên tập Fashion-MNIST:
Và đây là plot mình tự train để kiểm chứng trên tập Fashion-MNIST:
Hết.
Hãy like subscribe và comment vì nó miễn phí?
Nếu bạn muốn trao đổi thêm về chủ đề này, mình vô cùng chào đón các kiến thức mới hay góc nhìn lạ. Hiện tại mình đang làm bằng thạc sĩ về chủ đề này, nên mong có dịp diện kiến các cao nhân trong ngành 
All rights reserved
