HopSkipJumpAttack: Cách tấn công một mô hình học máy khi chỉ biết dữ liệu đầu ra.
Bài đăng này đã không được cập nhật trong 5 năm
Đây (vốn) là một bài trong series Báo khoa học trong vòng 5 phút.
Mở bài
Bạn muốn hack cho AI nhìn con mèo đoán ra con chó? Cũng dễ thôi nếu bạn có được cả mô hình và trọng số trong tay (ví dụ, sử dụng fast gradient sign method, với hướng dễn trên TensorFlow hoặc PyTorch, và đọc bài của anh Phạm Văn Toàn team mình tại đây). Tuy nhiên, cuộc đời thường không dễ vậy, và bạn phải đối mặt với các mô hình hộp đen — nghĩa là, bạn không biết cụ thể mô hình như thế nào, chỉ lấy được các kết quả đầu ra mà thôi. Ví dụ, bạn dùng một API nào đó như Google Vision chẳng hạn. Nếu như API đó cho bạn cả độ tự tin của nó về một quyết định (hay còn gọi là softmax probabilities) thì cũng vẫn dễ, vì bạn biết hướng gradient nào sẽ cho kết quả theo mong muốn, như mình đã viết ở đây. Nhưng mà Google Vision thì không cho gì ngoài kết quả phân lớp cuối cùng cả. Vậy thì làm sao bây giờ? Hãy đọc bài này để biết thêm chi tiết!
Paper được nhắc đến trong bài này có tên là HopSkipJumpAttack: A Query-Efficient Decision-Based Attack. Được viết bởi Chen et. al, University of California, Berkeley. Hiện đang là preprint chưa submit. Tên gọi cũ trong các phiên bản preprint trước là BoundaryAttack++.
Đây là video present paper (17 phút) cho biết ý tưởng nhanh của thuật toán (tuy nhiên nói khá sơ sài về mục boundary search):
Bài này mình sẽ không viết theo dàn bài bình thường vì nó quá dài và nhiều chứng minh toán học, và mỗi lần mình đọc thì mình buồn ngủ  Thay vì vậy, bài này sẽ giải thích thuật toán và ý tưởng đằng sau đó.
Thay vì vậy, bài này sẽ giải thích thuật toán và ý tưởng đằng sau đó.
Đồng thời, mình cũng có implementation tại repo của mình, để các bạn không phải cóp code tay từng section  .
.
Định nghĩa vài khái niệm
-
Bỏ qua tất cả các phần toán, bạn chỉ cần biết như sau:
- data gốc là ,
- data cần tìm là
sao cho mô hình bị tấn công phân lớp theo yêu cầu của chúng ta. Đối với targeted attack thì kết quả trả ra là một lớp cụ thể được xác định từ trước, còn đối với untargeted attack thì chỉ cần kết quả của khác với là được.
-
Với mỗi ảnh gốc , hàm cho biết data của chúng ta đã tấn công thành công chưa:
- nếu tấn công thành công (ra được kết quả phân lớp như mong muốn),
- nếu vẫn chưa thành công.
-
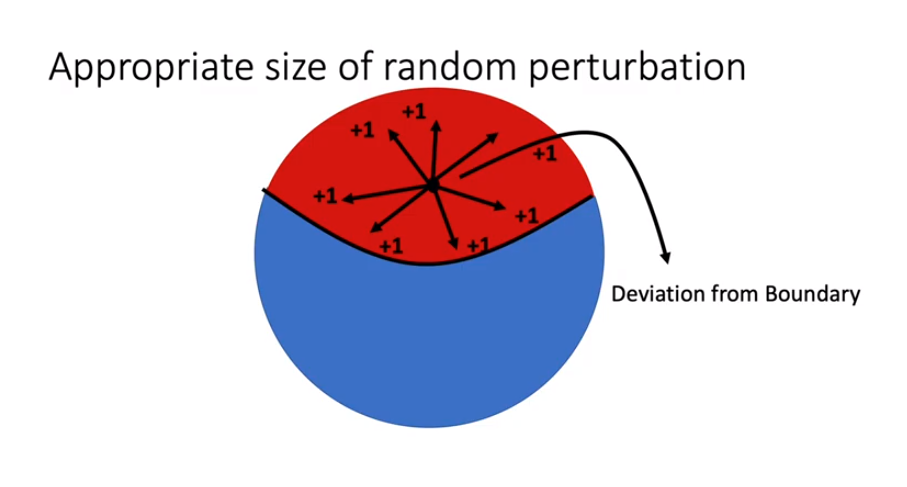
Tiếp theo, tìm đường biên giữa thành công và thất bại, hay chính là điểm phân chia sao cho . Lý do là vì chỉ ở trên đoạn đó mới có thể tìm được đường đi tiếp để đến vùng đất hứa (vùng màu xanh trong ảnh sau). Nếu ở ngoài đường biên, thì chuyện này sẽ xảy ra:
Từng bước của thuật toán
Mỗi lượt lặp của thuật toán có 3 bước, tuần tự theo 4 bức ảnh sau:
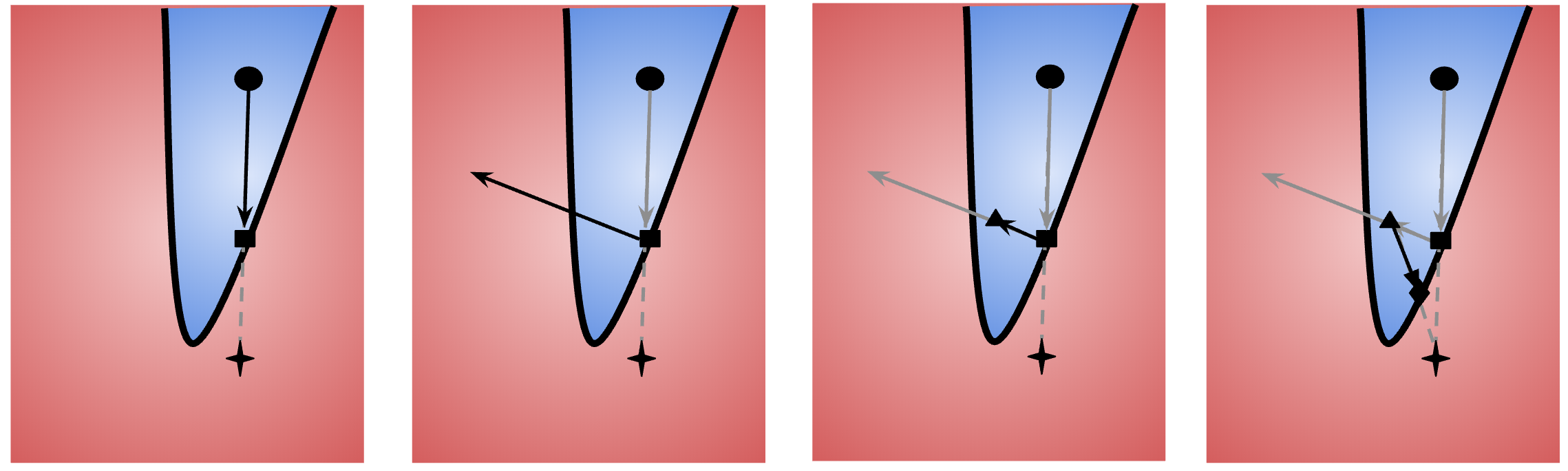
Ở vòng lặp thứ ta có điểm nằm ở vùng thành công, và nằm trên đường biên. Nói một cách khác là và . Trong đó, là một điểm bất kỳ thoả mãn điều kiện trên được chọn trước.
- Tìm điểm trên đường biên từ bằng tìm kiếm nhị phân:
-
Điểm nằm ở giữa và , và nằm trên cùng một đường thẳng; nói cách khác, chúng ta cần chọn để có .
-
Sử dụng tìm kiếm nhị phân để tìm ra giá trị sao cho . Trên thực tế, giá trị trên sẽ không bao giờ bằng (thường do API sẽ không cho biết cụ thể vậy), nên chỉ cần sai số trong một khoảng đủ nhỏ là được. Nghĩa là, với yêu cầu sai số tối đa xác định trước, sau khi ta có
- ,
- ,
- ,
thì chọn bất cứ giá trị nào trong khoảng cũng được.
-
- Ước lượng gradient: chốt trước một số lượng queries để ước lượng gradient ( là số query người dùng quyết định sử dụng ở vòng lặp đầu tiên), ta chọn ngẫu nhiên các vector đơn vị . Đồng thời chọn độ lớn của từng query trên , với là số chiều của vector ảnh đầu vào. Chúng ta tính:
Về ý tưởng thì đây là một ví dụ điển hình của phương pháp Monte Carlo: chúng ta giữ một danh sách các hướng đi đến được vùng , rồi lấy trung bình giữa chúng. Mỗi lần sample hướng đi , nếu đó là một hướng đi đến vùng thành công, thì chúng ta cho nguyên bản hướng đi đó (nhân với ) vào danh sách. Nếu không, chúng ta hãy đi hướng ngược lại (nhân với ).
Tuy nhiên, các ước lượng Monte Carlo đều bị vấn đề về variance cao. Vì vậy, đưa ra một công thức thay thế với variance thấp hơn:
với là xác suất chọn bừa một hướng mà hướng đó đưa ta đến vùng xanh.
Công thức trên có làm mình liên tưởng đến Bessel's correction, tuy nhiên mình không tìm được mối liên quan nào cả.
- Gradient Descent: chọn độ dài bước nhảy ban đầu , rồi tính
trong đó được đơn vị hóa tùy theo norm; cụ thể thì
Với bước nhảy vậy, có thể ta sẽ bị vọt quá vùng (hình thứ 3 trong ảnh minh họa.) Vì vậy, nếu điểm mới rơi vào vùng ngoài, chúng ta chia nửa độ dài bước nhảy cho đến khi nó vào vùng bằng 1 thì thôi (còn nếu từ đầu đã ok rồi thì không phải điều chỉnh step size.)
- Và quay lại bước 1. Do sau mỗi vòng lặp chúng ta đều nhận được một giá trị trong vùng thành công, nên chúng ta có thể dừng lúc nhận được một ảnh đủ gần với ảnh gốc.
Implementation cụ thể
Thực ra thì sau khi giải thích như trên thì phần còn lại dễ rồi  Code chúng ta cũng chia ra các bước như trên:
Code chúng ta cũng chia ra các bước như trên:
- Việc đầu tiên là tìm đường biên bằng binary search:
def binsearch_boundary(src_pt: np.ndarray,
dest_pt: np.ndarray,
threshold: float,
fn: Callable[[np.ndarray], bool]
) -> np.array:
'''
Find a point between two points that will lies on the boundary.
:param src_pt: point at which phi=0
:param dest_pt: point at which phi=1
:param threshold: gap between source point and destination point
:param fn: function that takes in a point and returns T/F if phi=1/0.
'''
while np.linalg.norm(dest_pt - src_pt) >= threshold:
midpoint = (src_pt + dest_pt) / 2
if fn(midpoint):
dest_pt = midpoint
else:
src_pt = midpoint
return dest_pt
- Sau đó là ước lượng gradient:
def estimate_gradient(orig_pt: np.ndarray,
step_size: np.ndarray,
sample_count: int,
fn: Callable[[np.ndarray], bool]
) -> np.ndarray:
'''
Estimate the gradient via Monte Carlo sampling.
:param orig_pt: point to estimate gradient at
:param step_size: length of each step in the proposed direction
:param sample_count: number of Monte Carlo samples
:param fn: function that takes in a point and returns T/F if phi=1/0.
'''
# sample directions
directions = np.random.randn(orig_pt.shape[0], sample_count)
directions /= np.linalg.norm(directions, axis=0)
# get phi values
values = np.empty((orig_pt.shape[0], 1), dtype=np.float)
for i in range(sample_count):
values[i, 0] = fn(directions[:, i]) * 2 - 1
# subtract from the mean
values -= np.mean(values)
# and average them
avg = np.sum(directions * values, axis=1) / (sample_count - 1)
# project them to unit L2
return avg / np.linalg.norm(avg)
- Cuối cùng là gradient descent:
def gradient_descent(orig_pt: np.ndarray,
grad: np.ndarray,
step_size: float,
fn: Callable[[np.ndarray], bool]
) -> np.ndarray:
'''
Do gradient descent on a point already on the boundary.
:param orig_pt: point to do gradient descent on
:param grad: the estimated gradient
:param step_size: initial step size to try
:param fn: function that takes in a point and returns T/F if phi=1/0.
'''
# find the step size to stay in phi=1
while True:
new_vector = orig_pt + step_size * grad
if fn(new_vector):
break
step_size /= 2
return new_vector
- Và gộp tất cả lại:
def hopskipjumpattack(orig_pt: np.ndarray,
fn: Callable[[np.ndarray], bool],
max_iter: Optional[int] = 100,
init_grad_queries: Optional[int] = 100,
binsearch_threshold: Optional[float] = 1e-6,
dest_pt: Optional[np.ndarray] = None,
start_iter: Optional[int] = 0
) -> np.ndarray:
'''
Implementation of the HopSkipJumpAttack.
:param orig_pt: point at which phi=0
:param fn: function that takes in a point and returns T/F if phi=1/0
:param max_iter: (Optional) maximum number of optimization iteration.
Default is 100.
:param init_grad_queries: (Optional) initial query count to estimate gradient
Default is 100.
:param binsearch_threshold: (Optional) the threshold to stop binary searching the boundary.
Default is 1e-6.
:param dest_pt: (Optional) point which phi=1.
If dest_pt is None, will be initialized to be a random vector.
:param start_iter: (Optional) last iteration count.
For cases when one restarts this iterative algo. Default is 0.
'''
d = orig_pt.shape[0]
# initialize a vector with phi=1
if dest_pt is None:
while True:
dest_pt = np.random.random_sample(d)
if fn(dest_pt):
break
for it in range(start_iter + 1, max_iter + 1):
print(f'Iter {it:03d}: ', end='')
# find the boundary
boundary = binsearch_boundary(orig_pt, dest_pt, binsearch_threshold, fn)
# if the error is too small, return as is
distance = np.linalg.norm(boundary - orig_pt)
if distance < binsearch_threshold:
print(distance)
print('Step size too small, terminating...')
# this works because we return the phi=1 endpoint in binsearch.
return boundary
# estimate the gradient
step_size = np.linalg.norm(dest_pt - orig_pt) / d
sample_count = int(init_grad_queries * it ** 0.5)
grad = estimate_gradient(boundary, step_size, sample_count, fn)
# and gradient descend
step_size = np.linalg.norm(boundary - orig_pt) / it ** 0.5
dest_pt = gradient_descent(boundary, grad, step_size, fn)
distance = np.linalg.norm(dest_pt - orig_pt)
print(distance)
return dest_pt
Thật là đơn giản, phải không nào?
Một số chú thích nho nhỏ
- Đã có 3 nơi khác có implementation cho thuật toán này từ chính tác giả bài báo (tác giả cũng submit pull request code của chính ổng lên 2 cái adversarial toolbox dưới đây). Tuy nhiên, cả 3 đều khá là khó sử dụng

- @Jianbo-Lab/HJSA: đây là repo gốc của tác giả. Khá dễ đọc, và giống i xì 2 phiên bản dưới.
- @tensorflow/cleverhans: hãy cài từ source github, vì phiên bản trên
pipvẫn chưa có HSJA. Documentations gần như không tồn tại. - @bethgelab/foolbox: ngày xưa có HSJA trên này, nhưng chắc bị gỡ từ một commit nào đó rồi.
- Implementation này không hỗ trợ norm, tuy nhiên thêm code đó vào cũng đơn giản thôi, và là bài tập về nhà cho bạn đọc.
Hết.
Hãy like subscribe và comment vì nó miễn phí?
All rights reserved
