Diffusion Models đang dần phổ biến. Nhiều trường đại học và khóa học đã đưa Diffusion Models vào chương trình giảng dạy. Mình viết bài này với hy vọng bài viết này sẽ có ích phần nào với các bạn muốn tìm hiểu về Diffusion Models.

Một số từ tạm dịch

• Diffusion: khuếch tán
• Quasi-static process: quá trình chuẩn tĩnh
• Thermodynamic Equilibrium: cân bằng nhiệt động học (NĐH)
• Forward Diffusion Process: quá trình khuếch tán thuận
• Reverse Diffusion Process: quá trình đảo ngược
• Transition kernel: nhân biến đổi.

Lời mở đầu

Diffusion Models đứng sau một số sản phẩm đình đám trong lĩnh vực sinh ảnh. Ứng dụng của loại mô hình này đã được mở rộng sang Object Detection, Image Segmentation,... Danh sách này nhiều khả năng sẽ còn mở rộng hơn nữa. Bài viết này sẽ giới thiệu từ ý tưởng cơ bản, những khái niệm trong nhiệt động học đã truyền cảm hứng cho Diffusion Models trong học sâu. Sau đó, ta sẽ đi đến lý thuyết và cách huấn luyện Diffusion Models trong học sâu.

I. Từ Nhiệt động học

Artificial Neural Network (Mạng nơ-ron nhân tạo), Genetic Algorithm (Giải thuật di truyền), Attention Mechanism (Cơ chế tập trung) là những ví dụ cho câu nói trên. Những phương pháp kể trên được lấy cảm hứng từ Khoa học thần kinh, Sinh học, Hệ thống thị giác của con người. Từ 2015, danh sách kể trên có thêm Diffusion Models. Ý tưởng cơ bản của phương pháp này được truyền cảm hứng từ Non-equilibrium Thermodynamics (Nhiệt động học không cân bằng), một lĩnh vực đã được nghiên cứu trong một thời gian dài. Cho đến hiện tại, những phương pháp SOTA đã có nhiều thay đổi làm cho cách hoạt động ngày càng khác xa so với Duffision trong Nhiệt động học. Dù vậy, việc hiểu Diffusion trong Nhiệt động học sẽ giúp ta hình dung được cách hoạt động của Diffusion Models trong Deep Learning. Trong phần này, chúng ta sẽ tìm hiểu về Diffusion trong nhiệt động học.

1. Diffusion là gì?

Diffusion (Khuếch tán) là hiện tượng chuyển động của các phân tử (hoặc ion, năng lượng...) từ vùng có mật độ cao hơn sang vùng có mật độ thấp hơn.

Hình 1. minh hoạ hiện tượng khuếch tán khi ta nhỏ một giọt thuốc nhuộm vào một cốc nước. Ban đầu giọt thuốc nhuộm tập trung ở 1 vùng nhỏ trong cốc nước với mật độ cao. Trong quá trình diffusion, thuốc nhuộm dần lan sang nhiều vùng trong cốc nước và mật độ của nó cũng loãng hơn. Sau một thời gian đủ lâu, thuốc nhuộm gần như sẽ phân bố đều trong cốc nước.

2. Cân bằng nhiệt động học là gì?

Một hệ (system) để được gọi là Cân bằng nhiệt động học cần đồng thời đạt được các điều kiện:

1. Cân bằng về nhiệt
2. Cân bằng cơ học
3. Cân bằng hoá học
4. Cân bằng pha

Hình 2: Hai hệ gồm khí bên trong bình. Bên trái: hệ cân bằng nhiệt. Bên phải: hệ không cân bằng nhiệt.

Chúng ta không cần thiết phải hiểu về 4 yếu tố kể trên. Nhưng sẽ tốt hơn nếu chúng ta hình dung được những yếu tố này. Ví dụ, xét đến yếu tố đầu tiên là Cân bằng nhiệt. Một hệ được gọi là Cân bằng nhiệt nếu nhiệt độ tại mọi điểm của hệ là giống nhau. Hình 2 minh hoạ một hệ cân bằng nhiệt(bên trái) và một hệ không cân bằng nhiệt (bên phải). Ta có thể thấy ở hình bên trái nhiệt độ tại các điểm của hệ khá "giống" nhau, còn ở hình bên phải nhiệt độ ở các điểm là rất khác nhau.

3. Quasi-static process

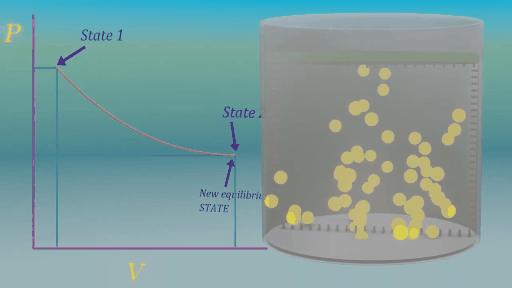
Như vậy ta đã biết một hệ cân bằng NĐH phải cân bằng về nhiều mặt. Xét một hệ cân bằng NĐH sử dụng các hạt đặt trên đỉnh pít tông để nén khí như trong hình 3. Giả sử ban đầu hệ có thể tích là $V_0$ là áp suất là $P_0$. Mỗi cặp ($P_t$, $V_t$) sẽ xác định một trạng thái.

Giả sử các hạt này là rất nhẹ và có rất nhiều hạt trên đỉnh pít tông. Nếu ta lấy ra một hạt trên đỉnh pít tông. Thể tích khí ở bên dưới sẽ nới rộng ra một chút là đạt được trạng thái cân bằng mới ($P_1$, $V_1$). Lấy ta tiếp tục việc lấy ra dần từng hạt một cách chậm rãi ta sẽ thu được ($P_2$, $V_2$), ($P_3$, $V_3$), ...($P_T$, $V_T$). Với T là số lần lấy hạt ra, và các trạng thái ($P_t$, $V_t$) đều cân bằng NĐH ($1 \leq t \leq T$). Quá trình chuyển từ trạng thái ($P_0$, $V_0$) sang ($P_T$, $V_T$) cực kỳ chậm như vậy là quasi-static và được minh họa ở hình 4.

Lý do người ta quan tâm đến quá trình quasi-static là tất cả Quá trình có thể đảo ngược (reversible process) đều là quá trình quasi-static. Nếu ta thêm lại dần dần các hạt đã lấy ra (từng chút từng chút một như lúc lấy ra) ta sẽ thu được các trạng thái trung gian. Trong điều kiện lý tưởng (các hạt vô cùng nhẹ, không có ma sát, thả không vận tốc ban đầu,...), các trạng thái trung gian sẽ chính là đảo ngược quá trình lấy ra ($P_T$, $V_T$), ($P_{T-1}$, $V_{T-1}$),...($P_1$, $V_1$), ($P_0$, $V_0$). Quá trình đảo ngược này được minh hoạ trong hình 5.

II. Diffusion trong Deep Learning

Trong phần này chúng ta sẽ tìm hiểu cách ý tưởng Diffusion trong Deep Learning được triển khai.

1. Ý tưởng tổng quan

Ý tưởng cơ bản của Diffusion trong Deep Learning là phá hủy cấu trúc của dữ liệu một cách có hệ thống và cực kỳ chậm thông qua Quá trình khuếch tán thuận. Quá trình này có tính lặp lại và được minh họa ở hình 6. Sau đó chúng ta sẽ học cách để đảo ngược quá trình này. Quá trình đảo ngược được minh họa ở hình 7.

Cụ thể hơn, chúng ta sẽ định nghĩa quá trình khuếch tán thuận. Quá trình này chuyển phân phối phân phối dữ liệu (vốn phức tạp) sang một phân phối đơn giản và có thể dễ dàng làm việc (như lấy mẫu). Sau đó ta sẽ học cách để đảo ngược quá trình này. Nếu làm được điều này(thực tế là làm được), Quá trình đảo ngược sẽ được sử dụng để sinh dữ liệu. Trong hai quá trình này, chúng ta chỉ cần sử dụng mạng neural để học cách thực hiện quá trình đảo ngược. Quá trình thuận hoàn toàn được cố định (fully defined, fixed) trước hoặc chỉ cần học một số biến phụ. Trong bài viết này, chúng ta sẽ cố định hoàn toàn Quá trình thuận.

Hy vọng đến đây chúng ta đã hình dung được phần nào ý tưởng diffusion trong Deep Learning. Sau đây chúng ta sẽ đi vào tìm hiểu chi tiết của hai quá trình trên.

2. Quá trình khuếch tán thuận

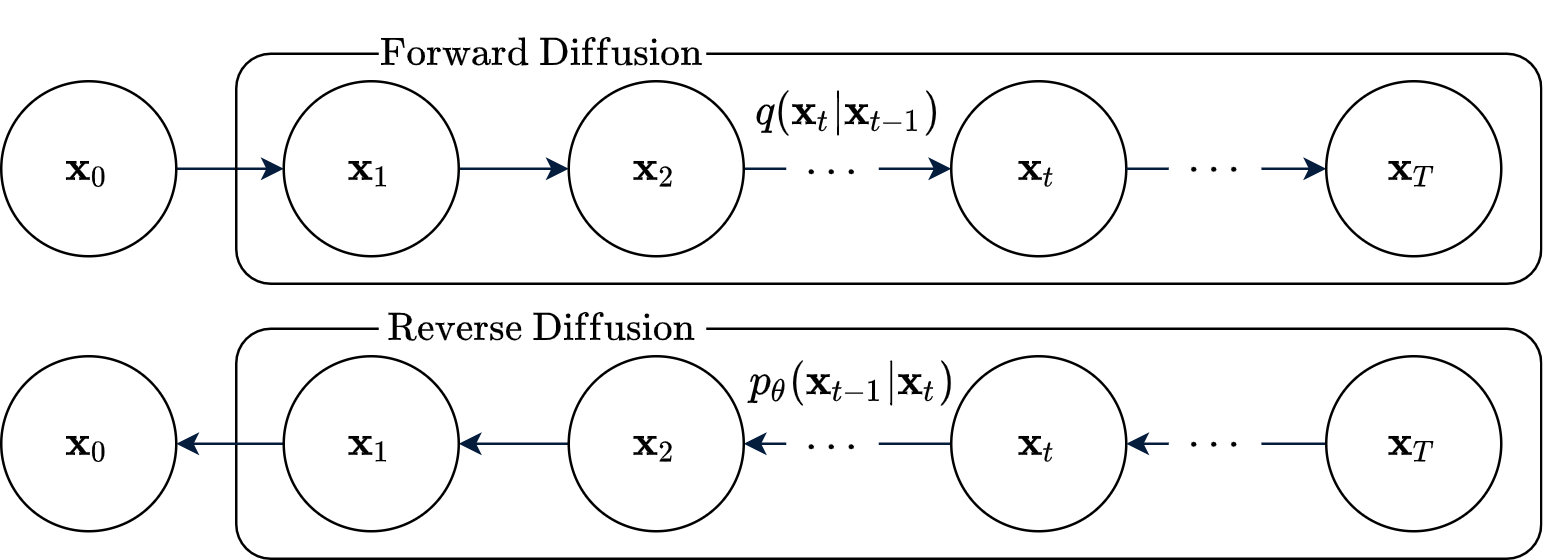
Quá trình thuận xuất phát từ phân phối của dữ liệu $q(x_0)$ và chuyển đổi dần dần thành phân phối có thể dễ dàng lấy mẫu $q(x_T) \approx \mathcal{N}(x_t; 0,\,\bold{I})$. Phân bố của $q(x_T)$ được chọn trước là một prior.

Trong hình 8, ở quá trình thuận, $x_0$ là dữ liệu; $x_1, x_2,...,x_T$ là các biến ẩn (latent) có cùng số chiều với $x_0$, T là số bước biến đổi. Quá trình khuếch tán được mô tả bằng một chuỗi Markov, nghĩa là trạng thái $x_{t}$ chỉ phụ thuộc vào $x_{t-1}$. Nhân biến đổi (transition kernel) của chuỗi $q(x_{t}|x_{t-1})$ được chọn sao cho:

$$q(x_{t}|x_{t-1}) = \mathcal{N}(x_t; x_{t-1}\sqrt{1 - \beta_t},\,\beta_t\bold{I}) \text{ với }\beta_t \in (0, 1)$$

$\beta_t$ là tốc độ khuếch tán ở bước $t$. Như vậy ta có thể tính $x_t$ dựa vào $x_{t-1}$ như sau:

$$x _ { t } = \sqrt { 1 - \beta _ { t } } x _ { t - 1 } + \sqrt { \beta _ { t } } \epsilon _ { t - 1 } \text{ với } \epsilon_{t-1} \sim \mathcal{N}(0, \bold{I})$$

Dựa vào công thức trên ta hoàn toàn có thể xác định được $x1$ từ $x0$, và sau đó xác định được $x2$ từ $x1$. Cứ như vậy tác sẽ tính được đến $x_T$ từ $x_{T-1}$. Nếu ta đặt $\alpha_t := 1- \beta_t$, $\bar{\alpha_t} := \prod_{s=1}^{t} \alpha_s$ và qua các phép biến đổi, ta có:

$$x_t = \sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}$$

Đây là một tính chất quan trọng của quá trình thuận. Tính chất này trên cho phép ta lấy mẫu được $x_t$ ở một bước t bất kỳ một cách trực tiếp (mà không phải đi từ bước 0, 1, 2,... rồi mới đến t). Đồng thời, công thức trên cũng cho ta thấy rõ được quá trình biến đổi dần dần phân phối dữ liệu thành nhiễu đẳng hướng. Cụ thể, vì $\beta_t$ < 1 với mọi $t$, nên khi $t$ tiến tới $T$ (ví dụ $T=1000$), $\sqrt{\bar{\alpha}_t}x_0$ sẽ tiến tới $0$ và $(1 - \bar{\alpha_t})\bold{I}$ sẽ tiến tới $\bold{I}$. Phần biến đổi để thu được công thức trên các bạn có thể xem ở dưới đây:

$$\begin{aligned} \mathbf{x}_t &= \sqrt{\alpha_t}\mathbf{x}_{t-1} + \sqrt{1 - \alpha_t}\boldsymbol{\epsilon}_{t-1} & \\ &= \sqrt{\alpha_t \alpha_{t-1}} \mathbf{x}_{t-2} + \sqrt{1 - \alpha_t \alpha_{t-1}} \bar{\boldsymbol{\epsilon}}_{t-2} & \\ &= \dots \\ &= \sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon} \\ q(\mathbf{x}_t \vert \mathbf{x}_0) &= \mathcal{N}(\mathbf{x}_t; \sqrt{\bar{\alpha}_t} \mathbf{x}_0, (1 - \bar{\alpha}_t)\mathbf{I}) \end{aligned}$$

Phân phối của quá trình thuận thu được bằng cách bắt đầu từ $q(x_0)$ và áp dụng nhân biến đổi bên trên qua T bước là:

$$q(x_{0...T}) = q(x_0) \prod_{t=1}^{T} q(x_{t}|x_{t-1})$$

Như đã nói ở trên, quá trình khuếch tán thuận mà chúng ta lựa chọn đã hoàn toàn được cố định. Như vậy chúng ta cần chọn trước các giá trị $\beta_1, \beta_2, ...\beta_T$, còn được gọi là lịch trình phương sai. Các giá trị này cần thoả mãn hai điều kiện:

1. Tổng lượng nhiễu $\beta_1, \beta_2, ...\beta_T$ phải đủ lớn giúp chuyển phân phối dữ liệu trở thành nhiễu đẳng hướng Gaussian.
2. Lượng nhiễu ở mỗi bước $\beta_t$ phải đủ nhỏ để có thể đảo ngược được. (Điều này tương tự như điều kiện để một quá trình là quasi-static ở phần I)

Giá trị của T phải được chọn trước. Để thoả mãn hai điều kiện trên thì T bắt buộc phải đủ lớn. T càng lớn thì ta có thể làm cho $\beta_t$ càng nhỏ. Để tóm tắt lại phần này mình xin trích lại slide của tác giả paper ở hình 9.

3. Quá trình đảo ngược

Quá trình đảo ngược cũng là một chuỗi Markov có những trạng thái như quá trình thuận nhưng theo chiều ngược lại, như được thể hiện ở hình 8. Quá trình đảo ngược còn được gọi quá trình sinh. Phân phối của quá trình sinh có được qua T bước áp dụng nhân biến đổi (tương tự quá trình thuận):

$$p(x_{0...T}) = p(x_T) \prod_{t=1}^{T} p(x_{t-1}|x_{t})$$

Với $p(x_T) = \mathcal{N}(x_T; 0,\,\bold{I})$. Để đảo ngược được chúng ta chỉ cần xác định nhân biến đổi ngược $p(x_{t-1}|x_{t})$ và biến đổi T bước để thu được $x_0$. Nếu $\beta_t$ nhỏ thì quá trình thuận và quá trình đảo ngược sẽ có cùng functional form. Vì nhân biến đổi thuận là Gaussian và $\beta_t$ đủ nhỏ, nên ta biết rằng nhân biến đổi nghịch cũng là một phân phối Gaussian. Còn mean và covariance của phân phối này thì chúng ta có thể sử dụng mạng neural để ước lượng. Ta có thể viết nhân biến đổi ngược dưới dạng tổng quát nhất như sau:

$$p(x_{t-1}|x_{t}) = \mathcal{N}(x_{t-1}; \bold{\mu}_\theta (x_t, t),\,\Sigma_\theta(x_t, t))$$

Chi phí tính toán của Diffusion Model chủ yếu đến từ chi phí tính toán của hai mô hình $\bold{\mu}_\theta (x_t, t)$ và $\Sigma_\theta(x_t, t)$. Để tóm tắt lại phần này, mình lại xin trích slide của tác giả ở hình 10.

Tips: hãy chú ý rằng các phân phối liên quan đến quá trình thuận là $q$, với quá trình đảo ngược là $p$

4. Hàm mục tiêu

Warning: Hãy sẵn sàng, đây là phần phức tạp nhất của Diffusion

4.1 Tối ưu likelihood

Việc huấn luyện được thực hiện bằng cách tối ưu chặn trên của Negative Log Likelihood:

$$L_{VLB} = \mathbb{E}_q[log \frac{q(x_{1:T}|x_0)}{p_\theta (x_{0:T})}] \ge \mathbb{E} [-\log{p_\theta(x_0)}]$$

Ta không thể tính toán hàm loss trên trực tiếp được vì không tính được hai phân phối thành phần trên. Do đó, ta cần biến đổi $L_{VLB}$ như sau để đưa về tính cách khoảng KL Divergence giữa các phân phối Gaussian (đó là lý do mà chúng ta phải thiết kế quá trình thuận thật cẩn thận để mọi thứ đều là Gaussian):

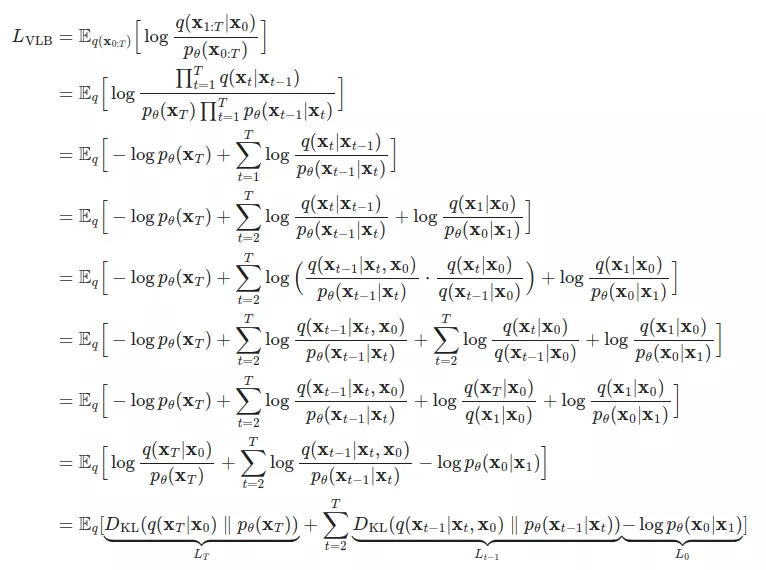
Hãy chú ý đến các thành phần ở dòng biến đổi cuối cùng. Ở các phần sau đây, chúng ta sẽ nói về từng thành phần này.

4.2 Thành phần $L_{T}$

$$L_T = D_\text{KL}(q(\mathbf{x}_T \vert \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_T))$$

Xét 2 thành phần của KL divergence bên trên. Thành phần đầu tiên, $q(\mathbf{x}_T \vert \mathbf{x}_0)$ chỉ phụ thuộc vào quá trình thuận và không chứa tham số tối ưu được. Thành phần thứ hai, $p_\theta(x_T)$ được chọn trước là $\mathcal{N}(0, \bold{I})$. Do đó, $L_{T}$ là hằng số trong quá trình huấn luyện và ta có thể bỏ qua thành phần này.

4.3 Thành phần $L_{0}$

Nếu như các transition kernel $p(x_{t-1}|x_t)$ với $t>1$ chiếu một không gian liên tục này sang không gian liên tục khác thì với $t=1$ nó cần chiếu một không gian liên tục về một không gian rời rạc (không gian của input).

Do sự khác biệt đó, thành phần cuối cùng của quá trình đảo ngược được tính theo cách riêng:

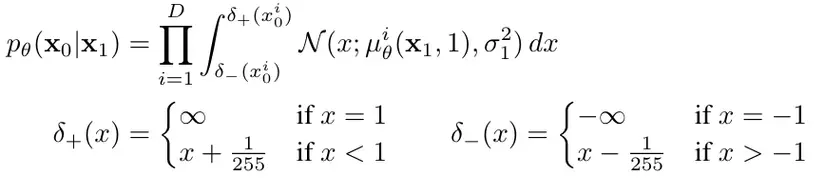
Trong đó, $D$ là chiều của dữ liệu, $i$ là chỉ số để lấy ra số chiều. Giả sử mỗi thành phần màu của ảnh đầu màu được chia vào 256 bin. Công thức trên tính xác suất $p_\theta(x_0|x_1)$ rơi vào bin đúng. Xác suất này tính được sử dụng CDF của phân phối Gaussian.

Công thức trên chỉ áp dụng với dữ liệu ảnh đầu vào gồm những số integer $\{0, 1, ..., 255\}$ được scale tuyến tính về $[-1, 1]$.

Code Pytorch tính thành phần này các bạn có thể xem ở đây

4.4 Thành phần $L_{t-1}$

$L_{t-1}$ là tổng của các KL divergence giữa $q(x_{t-1}|x_t, x_0)$ và $p_\theta(x_{t-1}, x_t)$. Hai thành phần này đóng vai trò tương ứng là target và prediction trong quá trình training. Như đã nói ở trên với $\beta_t$ đủ nhỏ, $q(x_{t-1}| x_t)$ là phân bố Gaussian. Cho dù vậy, chúng ta không thể dễ dàng ước lượng được phân phối này vì nó yêu cầu sử dụng cả tập dữ liệu. Tuy nhiên chúng ta có thể xác định được phân phối này khi đặt điều kiện trên $x_0$ bằng cách áp dụng quy tắc Bayes. Ta có $q(x_{t-1}| x_t, x_0) = \frac{q(x_t|x_{t-1}, x_0) q(x_t|x_0)}{q(x_{t-1}|x_0)}$. Cả ba thành phần để tính $q(x_{t-1}| x_t, x_0)$ lúc này để thuộc quá trình thuận và có thể xác định được dễ dàng. Qua các phép biến đổi ta có thể viết lại như sau:

$$q(x_{t-1}|x_t, x_0) = \mathcal{N}(x_{t-1}; \bold{\tilde{\mu}}_t(x_t, x_0),\,\tilde{\beta}_t \bold{I}) \text{ với } \tilde{\beta}_t = \frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \beta_t \text{ và } \bold{\tilde{\mu}}_t(x_t, x_0) = \frac{1}{\sqrt{\alpha_t}} (x_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha_t}}} \epsilon_t)$$

Chi tiết phần biến đổi để ra được công thức trên các bạn có thể xem thêm ở đây.

Để tối ưu thành phần chính $L_{t-1}$,chúng ta cần sử dụng một mạng neural $p_\theta(x_{t-1}|x_t)$ để ước lượng $q(x_{t-1}|x_t, x_0)$. Tổng quát nhất, $p_\theta(x_{t-1}|x_{t}) = \mathcal{N}(x_{t-1}; \bold{\mu}_\theta (x_t, t),\,\Sigma_\theta(x_t, t))$. Thực nghiệm cho thấy việc học $\Sigma_\theta(x_t, t)$ không cải thiện chất lượng sinh sample nên chúng ta cố định $\Sigma_\theta(x_t, t) = \sigma_t^2\bold{I}$

Áp dụng công thức tính KL Divergence cho 2 phân bố Gaussian ta có

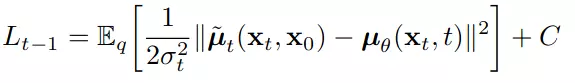
Trong đó C là hằng số. Nhìn vào công thức trên, chúng ta thấy rằng cách trực tiếp nhất là xây dựng mô hình dự đoán $\bold{\tilde{\mu}}_t(x_t, x_0)$. Tuy nhiên, các thành phần của $\bold{\tilde{\mu}}_t(x_t, x_0)$ đều đã biết trước chỉ trừ $\epsilon_t$. Nên thay vào đó ta có thể xây dựng mô hình dự đoán $\epsilon_t$, rồi sau đó gián tiếp dự đoán $\bold{\tilde{\mu}}_t(x_t, x_0)$. Ta chọn cách tham số hóa như sau:

$$\bold{\mu}_\theta(x_t, t) = \frac{1}{\sqrt{\alpha_t}} (x_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha_t}}} \epsilon_\theta(x_t, t))$$

Thay khai triển của ${\mu}_\theta(x_t, t)$ và $\bold{\tilde{\mu}}_t(x_t, x_0)$, ta có $L_{t-1} - C$ trở thành:

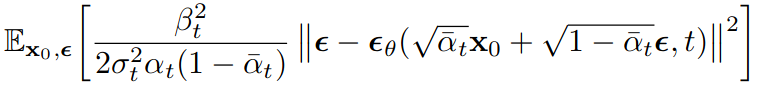
4.5 Đơn giản hóa hàm mục tiêu

Tổng kết lại các phần trên:

$$\begin{aligned} L_\text{VLB} &= L_T + L_{T-1} + \dots + L_0 \\ \text{trong đó } L_T &= D_\text{KL}(q(\mathbf{x}_T \vert \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_T)) \\ L_{t-1} &= D_\text{KL}(q(\mathbf{x}_{t-1} \vert \mathbf{x}_{t}, \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_{t})) \text{ với }2 \leq t \leq T-1 \\ L_0 &= - \log p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1) \end{aligned}$$

Vì $L_T$ là hằng số nên hàm tối ưu của chúng ta chỉ gồm 2 thành phần là $L_{t-1}$ và $L_0$. Tuy nhiên, thực nghiệm cho thấy rằng việc huấn luyện mô hình theo hàm mục tiêu được đơn giản hóa như sau cho kết quả tốt hơn:

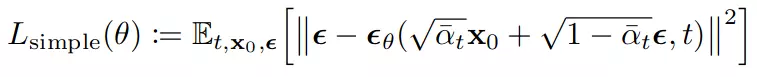
trong đó t là phân bố đều giữa 1 và T. Trường hợp $t=1$ tương ứng với $L_0$, giá trị của tích phân được xấp xỉ bằng khai triển Taylor của hàm mật độ xác suất Gaussian. Với t > 1, $L_{simple}$ tương ứng với phiên bản không trọng số(hay có thể coi là đánh trọng số lại) của $L_{t-1}$.

Việc chọn hàm đơn giản như trên cho kết quả tốt hơn có thể được giải thích là do nó làm giảm ảnh hưởng khi giá trị $t$ nhỏ. Giá trị của $t$ nhỏ tương ứng với ảnh ít nhiễu. Từ đó, giúp mô hình tập trung hơn vào việc học dự đoán nhiễu khi $t$ lớn. Vì khi $t$ lớn thì lượng nhiễu trong ảnh cũng lớn nên khó để dự đoán hơn.

5. Kiến trúc mô hình

Kiến trúc mô hình sử dụng trong Diffusion Models cần có chiều của đầu ra phải giống với chiều của đầu vào. Do đó, các mạng tương tự U-Net thường được sử dụng. Những mô hình này có một vài thay đổi so với thông thường để thông tin $t$ làm một đầu vào.

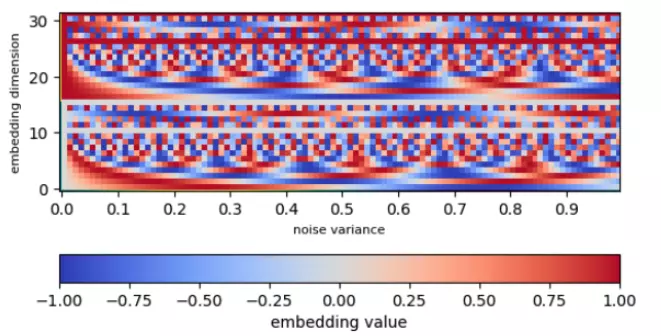
Thông tin về thời gian $t$ cũng có thể được đại diện bằng noise variance. Chúng sẽ được biến đổi bằng Sinusoidal Embedding trước khi đưa vào U-Net. Ý tưởng phía sau là biến đổi một giá trị scalar về vector nhiều chiều hơn để tạo ra một biểu diễn phức tạp hơn.

Hai hình dưới đây minh họa một ví dụ về kiến trúc U-Net sử dụng trong Diffusion Models và giá trị của embeddings khi đưa vào.

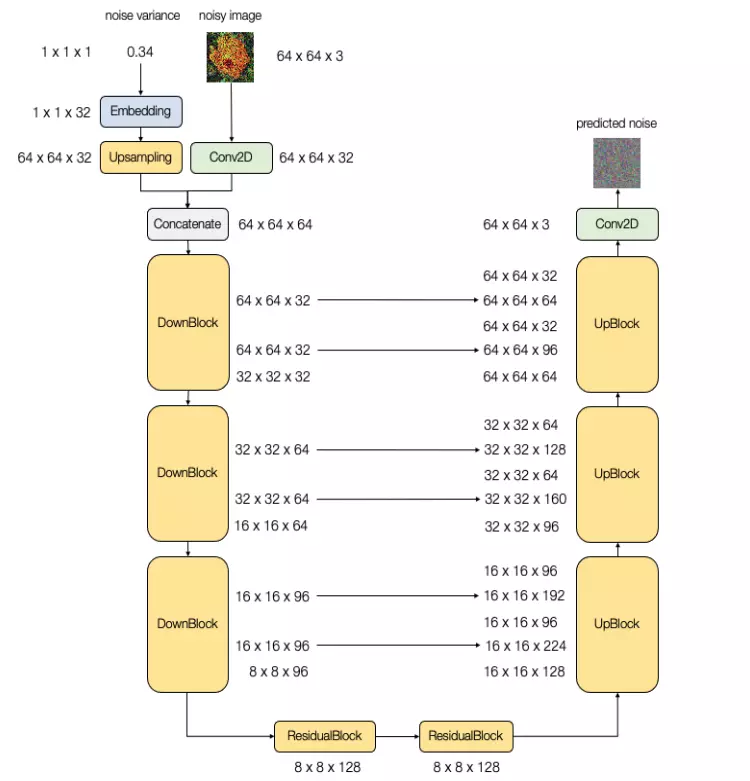
6. Sinh ảnh (sẽ cập nhật thêm sau)

Sau khi có được mô hình để dự đoán $p(x_{t-1}|x_t)$. Ta có thể dễ dàng sinh dữ liệu mới theo các bước sau:

Hints: dòng thứ 4 là do $p_\theta(x_{t-1}|x_{t}) = \mathcal{N}(x_{t-1}; \bold{\mu}_\theta (x_t, t),\,\sigma_t^2\bold{I})$

Tra cứu (sẽ cập nhật thêm sau)

Phần cuối cũng bài viết cung cấp mục tra cứu và giải thích các ký hiệu phổ biến được sử dụng.

Ký hiệu	Ý nghĩa	Ví dụ
$T$	số timestep tối đa	$T=1000$
$\beta_t$ $(t \in [1,T])$	phương sai của nhiễu thêm được vào ở timestep $t-1$ sang $t$	$\beta_0 = 0.0001$ và $\beta_{T} = 0.02$ (linspace)
$1- \bar{\alpha_t}$	phương sai của tổng lượng nhiễu ở timestep $t$	$1-\bar{\alpha_0}=$ 1e-05 và $1-\bar{\alpha_{T}}$ = 0.999957

Lời kết

Trong bài này mình đã trình bày cơ bản về Diffusion Models. Phần mối liên giữa Khuếch tán trong Nhiệt động học và trong Học sâu mình không trình bày cụ thể mà để mở để các bạn có sự liên hệ, tưởng tượng riêng của mình. Hy vọng các bạn thấy bài viết này hữu ích. Nếu có vấn đề hay thắc mình gì đừng ngại cho mình biết ở phần comment để mình cải thiện ở các phần sau nhé. Cảm ơn các bạn đã đọc bài. Hẹn gặp lại ở bài viết sau về chủ đề Diffusion Models.

Toàn bộ credit thuộc về các nguồn tài liệu tham khảo. Mình recommend các bạn đọc tài liệu số 6.

Tài liệu tham khảo

• [1] [2015 ICML] Deep Unsupervised Learning using Nonequilibrium Thermodynamics
• [2] Deep Unsupervised Learning using Nonequilibrium Thermodynamics
• [3] Denoising Diffusion Probabilistic Models
• [4] Quasi-Equilibrium and Thermodynamic Equilibrium
• [5] Quasi-static process
• [6] What are Diffusion Models?
• [7] Paper reading DDPM
• [8] Improved Denoising Diffusion Probabilistic Models
• [9] Generative Deep Learning