Lý thuyết xác suất (P1)
Bài đăng này đã không được cập nhật trong 4 năm
I.Tại sao dùng lý thuyết xác suất trong machine learning?
Xung quanh ta luôn có đầy những điều không chắc chắn: hôm nay trời có mưa không? Bộ phim kia liệu có được đón nhận? Giá cổ phiếu hôm nay... Lý thuyết xác suất đóng một vai trò trung tâm trong các thuật toán machine learning để có thể đưa ra các dự đoán dễ xảy ra nhất. Trong bài viết này và các bài viết sau tôi sẽ trình bày các khái niệm cơ bản nhất và ứng dụng của lý thuyết xác suất trong machine learning.
II.Các khái niệm cơ bản của lý thuyết xác suất
1. Không gian mẫu
Không gian mẫu là tập hợp của tất cả các khả năng có thể. Ví dụ khi tung 1 con súc sắc 6 mặt không gian mẫu Ω là {1, 2, 3, 4, 5, 6}.
2.Sự kiện
Sự kiện là một tập con của không gian mẫu. Ví dụ tung súc sắc như trên thì sự kiện tung ra mặt lẻ là tập hợp {1, 2, 3}. Xác suất được gán với 1 sự kiện.
3.Các tiên đề của xác suất
- Xác suất luôn không âm
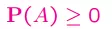
- Xác suất của không gian mẫu = 1
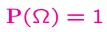
- Cộng xác suất nếu 2 sự kiện A và B không giao nhau:
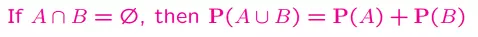 Từ các tiên đề trên ta có thể chứng minh được các điều sau
Từ các tiên đề trên ta có thể chứng minh được các điều sau
- A ⊂ B => P(A) < P(B)
- P(A∪B) = P(A) + P(B) - P(A∩B)
- P(A∪B) ≤ P(A) + P(B)
4.Ví dụ
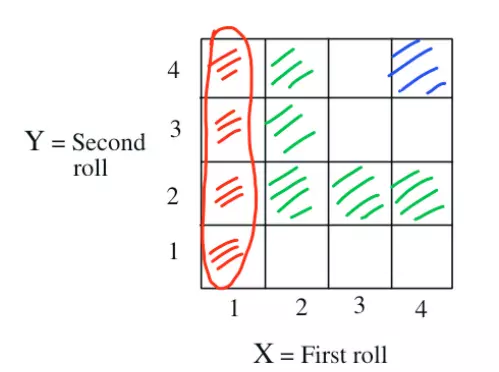
Tung con xúc sắc bốn mặt 2 lần. Gọi X là kết quả của lần tung đầu tiên và Y là kết quả ở lần tung thứ hai. Vậy ta có các khả năng (1, 1) , (2, 1), (3, 1), (4, 1) ... Giả sử xác suất của các khả năng là như nhau.
Ta có P(X = 1) = 4 . 1/16 = 4/16 (màu đỏ)
Nếu Z = min(X, Y)
P(Z = 4) = 1/16 (màu xanh nước biển)
P(Z = 2) = 5 . 1/16 = 5/16 (màu xanh lá cây)
5.Lý giải cho xác suất
Một số người nhìn nhận về xác suất như tần số. Ví dụ nếu nói là xác suất để tung 1 đồng xu ra mặt ngửa là 50% thì có nghĩa là nếu tung rất nhiều lần rồi đem số lần ra mặt ngửa chia cho tổng số lần sẽ ra xấp xỉ 50%. Tuy nhiên có những sự kiện mà ta không thể làm thí nghiệm được. Ví dụ theo như cách nhìn nhận kiều tần số như trên thì có thể lý giải như thế nào về xác suất để tổng thống Mỹ sẽ tái đắc cử? Do đó mà xác suất nên được nhìn nhận như là cách để thể hiện niềm tin của chúng ta về một sự kiện nào đó. Ví dụ P(tổng thống Mỹ tái đắc cử) = 0.7 tức là chúng ta tin tưởng rằng có khoảng 70% khả năng là tổng thống Mỹ sẽ được đắc cử. Hoặc nếu đặt cược cửa 50:50 thì ta sẽ đặt cho khả năng tổng thống Mỹ tái đắc cử vì chúng ta có niềm tin hơn là khả năng kia.
III.Xác suất có điều kiện
1. Khái niệm
Xác suất có điều kiện giúp ta cập nhật lại niềm tin của chúng ta về một sự kiện nếu ta có thêm một dữ liệu gì đó.
Ví dụ khi khi cả 12 khả năng dưới đây là như nhau
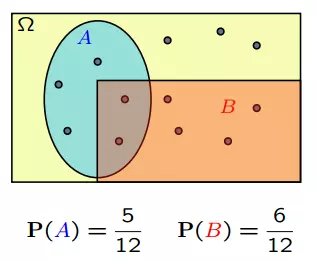 Khi ta biết được là B sẽ xảy ra. (P(A | B) là xác suất của A nếu ta biết B xuất hiện)
Khi ta biết được là B sẽ xảy ra. (P(A | B) là xác suất của A nếu ta biết B xuất hiện)
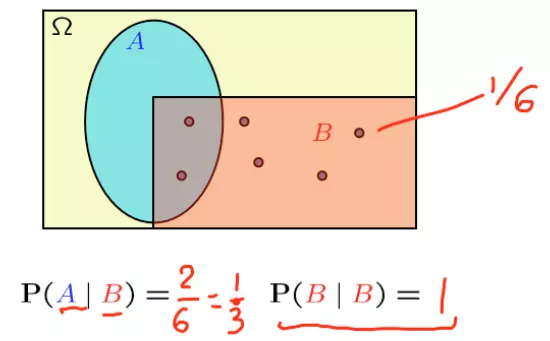 Bởi vì ta chỉ quan tâm tới 6 chấm của sự kiện B. Trong đó thì có 2 chấm của sự kiện A.
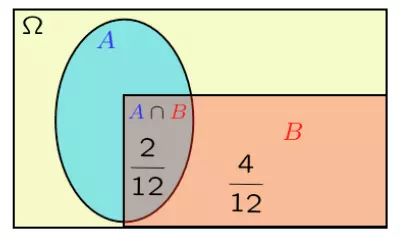
Ví dụ trên hướng ta tới định nghĩa cho xác suất có điều kiện
Bởi vì ta chỉ quan tâm tới 6 chấm của sự kiện B. Trong đó thì có 2 chấm của sự kiện A.
Ví dụ trên hướng ta tới định nghĩa cho xác suất có điều kiện
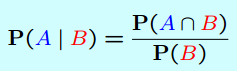 (chỉ định nghĩa khi P(B) > 0)
Để hiểu thêm
(chỉ định nghĩa khi P(B) > 0)
Để hiểu thêm
2. Ví dụ
Các bạn hãy thử làm thử ví dụ dưới đây.
Ta tung 2 lần một con xúc sắc bốn mặt.
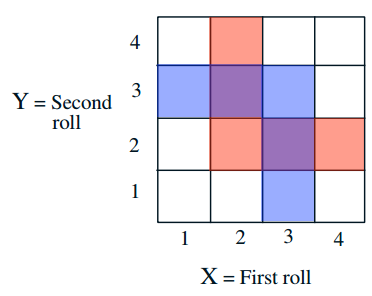 Giả sử B là sự kiện min(X, Y) = 2 (màu đỏ)
Nếu M là max(X, Y)
Tính P(M = 1 | B) và P(M = 3 | B) trong đó M = 1 là sự kiện tương ứng với ô ở góc dưới cùng bên trái, M = 3 tương ứng với các ô màu xanh
(Đáp án: P(M = 1 | B) = 0 và P(M = 3 | B) = 2/5)
Giả sử B là sự kiện min(X, Y) = 2 (màu đỏ)
Nếu M là max(X, Y)
Tính P(M = 1 | B) và P(M = 3 | B) trong đó M = 1 là sự kiện tương ứng với ô ở góc dưới cùng bên trái, M = 3 tương ứng với các ô màu xanh
(Đáp án: P(M = 1 | B) = 0 và P(M = 3 | B) = 2/5)
3. Tính chất
Các tính chất của xác suất có điều kiện tương tự như xác suất bình thường (chúng ta chỉ cần tưởng tượng là các sự kiện bên trái | sống ở một không gian mẫu mà sự kiện bên phải | xảy ra)
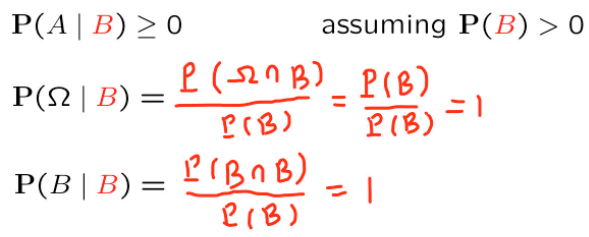
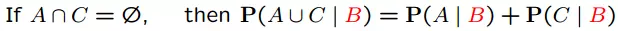
IV.Định lý xác suất tổng hợp
1.Định lý
Để tìm xác suất của sự kiện B, ta có thể chia không gian mẫu Ω thành các phần A1, A2, A3, ... và tính xác suất của B rơi vào mỗi phần đó.
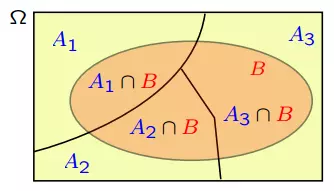 Như trong hình ta có
Như trong hình ta có
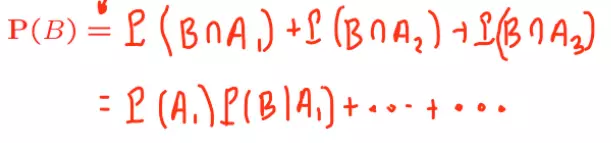 Vì các sự kiện A1 ∩ B, A2 ∩ B ... đều không giao nhau và hợp A1, A2, A3... là cả không gian mẫu.
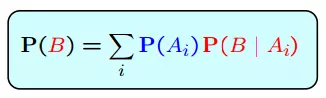
Vì P(A1 ∩ B) = P(Ai) P(B | Ai) nên ta có định lý xác suất tổng hợp sau đây
Vì các sự kiện A1 ∩ B, A2 ∩ B ... đều không giao nhau và hợp A1, A2, A3... là cả không gian mẫu.
Vì P(A1 ∩ B) = P(Ai) P(B | Ai) nên ta có định lý xác suất tổng hợp sau đây
2.Ví dụ
Tôi có 3 chiếc cặp, mỗi chiếc chứa 100 viên bi
- Cặp 1 có 75 đỏ và 25 xanh
- Cặp 2 có 60 đỏ và 40 xanh
- Cặp 3 có 45 đỏ và 55 xanh Nếu tôi chọn 1 trong 3 chiếc cặp ngẫu nhiên và từ chiếc cặp đó cũng chọn bi ngẫu nhiên thì xác suất để ra bi đỏ là bao nhiêu?
Lời giải Gọi B là sự kiện chọn được bi đỏ. Ai là sự kiện bi đó được chọn từ cặp i. Ta có
- P(B | A1) = 0.75
- P(B | A2) = 0.60
- P(B | A3) = 0.45 Cách chọn chia không gian mẫu thành A1, A2, A3 là hợp lệ vì các sự kiện đó không giao nhau (chỉ có thể chọn được từ 1 cặp) và tất cả hợp lại thành tất cả các sự kiện có thể (một cặp nào đó phải có bi được chọn). Dùng định lý xác suất tổng hợp ta có thể viết. P(B) = P(B | A1)P(A1) + P(B | A2)P(A2) + P(B | A3)P(A3) = (0.75)1/3 + (0.60)1/3 + (0.45)1/3 = 0.60
V.Kết luận
Trong bài viết này tôi đã trình bày các khái niệm cơ bản nhất của lý thuyết xác suất, xác suất có điều kiện và định lý xác suất tổng hợp. Ở các bài viết tiếp theo tôi sẽ trình bày tiếp các điều thú vị khác của lý thuyết xác suất và ứng dụng của nó trong machine learning.
VI.Tham khảo
- MITx: 6.041x Introduction to Probability - The Science of Uncertainty
- https://www.probabilitycourse.com/chapter1/1_4_2_total_probability.php
All rights reserved