Neural Network Fundamental 4: Gradient descent, back propagation
Bài đăng này đã không được cập nhật trong 4 năm
I. Gradient descent
Giả sử ta muốn minimize . Nếu đây là 1 hàm sỗ phức tạp thì việc tìm 1 công thức tính cho J min là không dễ dàng. Gradient descent là thuật toán bắt đầu từ 1 giá trị nào đó của rồi đi từ từ từng bước một, mỗi bước lại update lại các parameter này và cuối cùng sẽ một giá trị mà J min.
Câu hỏi đặt ra là với mỗi bước sẽ đi như nào. Để đơn giản, xét ví dụ là hàm số 1 biến số
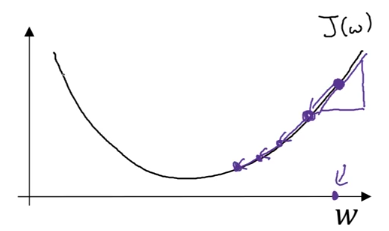 Từ giá trị ban đầu (chấm bên phải ngoài cùng) ở mỗi bước ta update theo rule sau
Repeat {
}
Trong đó là learning rate quyết định ta bước mỗi bước ngắn hay dài
> 0 tức J tăng lên khi ta tăng w lên 1 khoảng rất nhỏ nên ta trừ đi 1 số dương là
Từ giá trị ban đầu (chấm bên phải ngoài cùng) ở mỗi bước ta update theo rule sau
Repeat {
}
Trong đó là learning rate quyết định ta bước mỗi bước ngắn hay dài
> 0 tức J tăng lên khi ta tăng w lên 1 khoảng rất nhỏ nên ta trừ đi 1 số dương là
< 0 tức J tăng lên khi ta giảm w lên 1 khoảng rất nhỏ nên ta trừ đi 1 số âm là nghĩa là cộng thêm Khi w gần tới giá trị J min thì độ dốc của hàm số nhỏ đi do đó các bước ta đi cũng nhỏ đi
II. Gradient descent for Neural Network
Chúng ta hãy nhắc lại một chút ở bài trước, loss function cho tất cả m training example
Trong đó là loss function tính cho training example i
Mục tiêu của chúng ta là tìm giá trị của sao cho J nhỏ nhất.
Thực hiện gradient descent mỗi bước ta tính partial derivative (đạo hàm riêng) của từng layer: ,
Repeat {
, , ...
$W^{[1]} = W^{[1]} - \alpha,dW^{[1]} $
$b^{[1]} = b^{[1]} - \alpha,db^{[1]} $
...
}
là ma trận có cùng chiều với chứa đạo hàm riêng của từng phần tử trong với
là vector có cùng chiều với chứa đạo hàm riêng của từng phần tử trong với
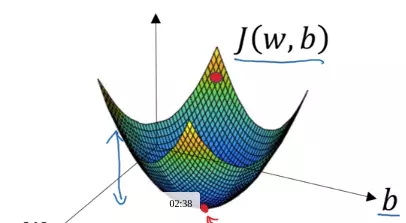
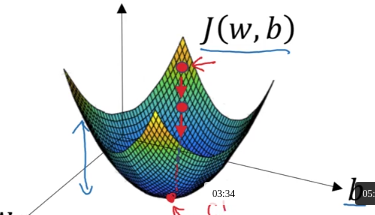
Nếu tập hợp tất cả các parameter thành 1 vector D. Kiến thức trong giải tich nhiều biến số cho ta biết là vector gradient của D cho ta hướng mà hàm số tăng nhanh nhất. Nên nếu ta muốn chiều mà hàm số đang giảm, ta update các parameter đó bằng cách trừ đi learning rate partial derivative
III. Backward propagation
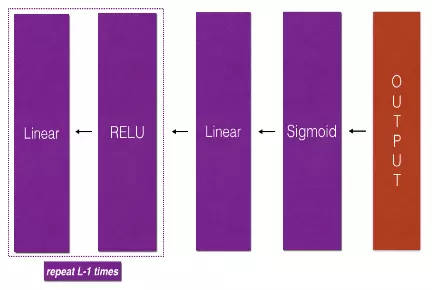
Ta nhắc lại một chút, forward propagation thực hiện việc tính toán input layer hidden layer nếu như đã biết trước của mỗi layer
for l = 1..L
Thuật toán gradient descent cần tính và ở mỗi lớp để có thể update . Backward propagation theo đúng tên gọi của nó đi từ output layer hiddenlayer input layer, và dựa vào các giá trị của và đã tính toán ở mỗi lớp trong forward propagation mà tính được và
 Dưới đây tôi sẽ trình bày công thức tính, phần chứng minh sẽ để ở bài kế tiếp
Dưới đây tôi sẽ trình bày công thức tính, phần chứng minh sẽ để ở bài kế tiếp
Back propagation cho 1 training example
Đạo hàm của ở lớp cuối cùng Với mỗi lớp l (nhân từng phần từ của 2 vector với nhau, nếu l = L thì ta dùng công thức ở trên) $dW^{[l]} = dz^{[l]} a^{[l - 1]T} $ Trong đó và đã biết từ forward propagation Biết được ta và các giá trị của lớp đó (forward propagation) ta lại tính được , ,
Back propagation cho m training example
Đạo hàm của ở lớp cuối cùng (Z là ma trận mà các cột là các neural của 1 lớp của mỗi training example) Với mỗi lớp l (nhân từng phần tử của 2 ma trận với nhau, nếu l = L thì ta dùng công thức ở trên) tổng các cột của vector Biết được ta và các giá trị của lớp đó (forward propagation) ta lại tính được , ,
Tham khảo
- Coursera deep learning
- Hugo Larochelle Neural Network
All rights reserved