I. Neural Network Representation for 2 layers

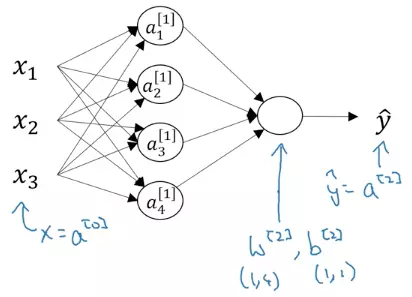
Dưới đây là biểu diễn của mạng neural với 2 lớp

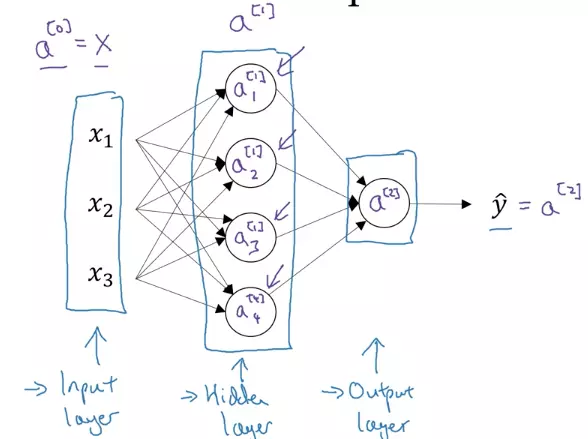
• Các input feature $x_1$, $x_2$, ... được xếp chồng lên nhau và được gọi là input layer
• Lớp tiếp theo chứa các node là sự kết hợp của các node trong input layer được gọi là hidden layer
• Lớp cuối cùng chỉ có một node, chứa giá trị dự đoán $\hat{y}$ được gọi là output layer Để tiện cho việc tính toán, ta sẽ vector hóa các node trong mỗi layer bằng các vector $a$
• Số ở trên dấu ngoặc vuông trên đầu của $a$ thể hiện số layer. Số layer được đánh số từ 0 ở input layer
• Số ở dưới của $a$ thể hiện node thứ mấy trong lớp đó Ví dụ vector $a$ ở input layer $a^{[0]} = \begin{bmatrix}a^{[0]}_1\\a^{[0]}_2\\ a^{[0]}_3\end{bmatrix}$ Mạng neural như trên hình được gọi là mạng neural 2 lớp vì chúng ta không đếm input layer

II.Forward Propagation with 2 layers Neural Network

Forward Propagation hiểu nôm na là bắt đầu từ input, ta sẽ tính toán giá trị các neural của từng lớp một, đến cuối cùng sẽ tính ra giá trị của lớp output. Như đã nói ở phần Artificial Neural trong phần 1 mỗi giá trị $a$ ở một neural (node) sẽ được tính toán qua 2 bước 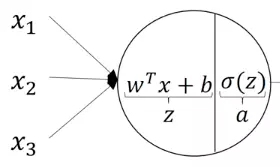$z = \sum_{i}w_ix_i + b = \bold{w}^\intercal\bold{x}$ + b $a = \sigma(z)$ Trong đó z gọi là giá trị pre-activation, còn a gọi là giá trị activation, $w$ và $b$ là các parameter của neural network. Mục đích cuối cùng của chúng ta là optimize các parameter này sao cho neural network có thể output một cách chính xác nhất

Tính toán ở hidden layer

Dựa vào nguyên tắc trên, ta bắt đầu tính toán ở neural đầu tiên của hidden layer

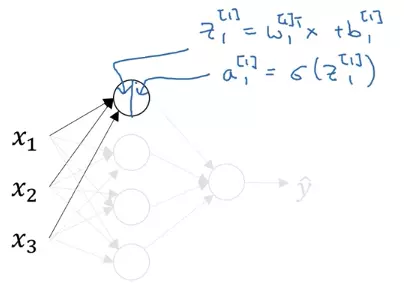
• $z^{[1]}_1$: số ở trên cho ta biết $z$ thuộc lớp thứ 1, số ở dưới thể hiện đây là giá trị pre-activation của neural đầu tiên của lớp này
• $w^{[1]}_1$: số ở trên thể hiện đây là vector $w$ để tính toán lớp thứ 1, số ở dưới thể hiện w này là để tính toán neural thứ 1
• $b^{[1]}_1$ và $a^{[1]}_1$: cũng thể hiện tương ứng

Tương tự như vậy ta tính toán cho neural thứ 2 của hidden layer 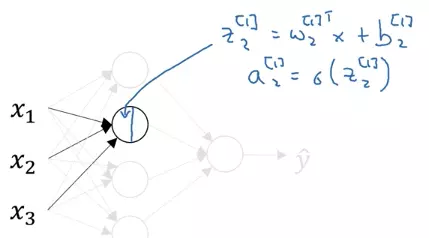Tính toán hết với cả 4 neural của hidden layer ta được $z^{[1]}_1$ = $w^{[1]\intercal}_1x + b^{[1]}_1, a^{[1]}_1 = \sigma(z^{[1]}_1)$ $z^{[1]}_2$ = $w^{[1]\intercal}_2x + b^{[1]}_2, a^{[1]}_2 = \sigma(z^{[1]}_2)$ $z^{[1]}_3$ = $w^{[1]\intercal}_3x + b^{[1]}_3, a^{[1]}_3 = \sigma(z^{[1]}_3)$ $z^{[1]}_4$ = $w^{[1]\intercal}_4x + b^{[1]}_4, a^{[1]}_4 = \sigma(z^{[1]}_4)$ Trong code ta có thể dùng vòng lặp for để tính các giá trị z và a của hidden unit, nhưng làm như vậy mất rất nhiều thời gian. Do đó, ta sẽ vector hóa việc tính toán lại Đầu tiên ta sẽ xếp các vector $w^{[1]\intercal}_1$, $w^{[1]\intercal}_2$, $w^{[1]\intercal}_3$, $w^{[1]\intercal}_4$ lại thành matrix $W^{[1]}$, các giá trị của b thành vector $b^{[1]}$. Số index trên đầu thể hiện đây là các parameter của lớp 1 $W^{[1]} =\begin{bmatrix}-w^{[1]\intercal}_1-\\-w^{[1]\intercal}_2-\\-w^{[1]\intercal}_3-\\-w^{[1]\intercal}_4-\end{bmatrix} \qquad b^{[1]} = \begin{bmatrix}b^{[1]}_1\\b^{[1]}_2\\ b^{[1]}_3\\b^{[1]}_4\end{bmatrix}$ Ta để ý matrix $W^{[1]}$ có chiều là 4 x 3 = số neural của lớp hiện tại (hidden layer) x số neural lớp trước (input layer) Từ đó ta có thể biểu diễn các giá trị của vector $z^{[1]}$ $z^{[1]} = \begin{bmatrix}z^{[1]}_1\\z^{[1]}_2\\ z^{[1]}_3\\z^{[1]}_4\end{bmatrix} = \begin{bmatrix}-w^{[1]\intercal}_1-\\-w^{[1]\intercal}_2-\\-w^{[1]\intercal}_3-\\-w^{[1]\intercal}_4-\end{bmatrix}\begin{bmatrix}x_1\\x_2\\ x_3\end{bmatrix} + \begin{bmatrix}b^{[1]}_1\\b^{[1]}_2\\ b^{[1]}_3\\b^{[1]}_4\end{bmatrix}$

Và vector $a^{[1]}$ $a^{[1]} = \begin{bmatrix}a^{[1]}_1\\a^{[1]}_2\\ a^{[1]}_3\\a^{[1]}_4\end{bmatrix} = \sigma(z^{[1]})$

Tính toán ở output layer

Output layer sẽ nhận vector $a^{[1]}$ của hidden layer làm input và thực hiện tính toán tương tự như ở hidden layer ta có $z^{[2]} = W^{[2]}a^{[1]} + b^{[2]}$ $a^{[2]} = \hat y = \sigma(z^{[2]})$ Để ý chiều của $W^{[2]}$ là 1 x 4 , còn của $b^{[2]}$ là 1 x 1 Tóm tắt lại ở cả 2 bước thì forward propagation thức hiện tính toán $x \rightarrow \hat y$ như sau $z^{[1]} = W^{[1]}a^{[0]} + b^{[1]} \quad (a^{[0]} = x)$
$a^{[1]} = \sigma(z^{[1]})$

$z^{[2]} = W^{[2]}a^{[1]} + b^{[2]}$ $a^{[2]} = \hat y = \sigma(z^{[2]})$

Vector hóa với nhiều training example

Trên đây ta thực hiện forward propagation với một training example từ input $x$ tính toán ra giá trị dự đoán $\hat y$: $x \rightarrow \hat y$. Thực hiện với m training examples khác nhau ta lặp lại quá trình đó m lần $x^{(1)} \rightarrow a^{[2](1)} = \hat y^{(1)}$ $x^{(2)} \rightarrow a^{[2](2)} = \hat y^{(2)}$ $\vdots$ $x^{(m)} \rightarrow a^{[2](m)} = \hat y^{(m)}$ Trong đó các giá trị trọng () ở trên thể hiện đây là đây là training example thứ mấy. Ví dụ $a^{[2](2)}$ là output của training example thứ 2 Nếu dùng vòng lặp for để thực hiên forward propagation với tất cả training example: for i = 1 to m: $\quad z^{[1](i)} = W^{[1]}x^{(i)} + b^{[1]}$
$\quad a^{[1](i)} = \sigma(z^{[1](i)})$ $\quad z^{[2](i)} = W^{[2]}a^{[1](i)} + b^{[2]}$ $\quad a^{[2](i)} = \sigma(z^{[2](i)})$ Chú ý là các parameter $W$ và $b$ giữ nguyên giá trị với các training example khác nhau Như trên đã nói việc dùng vòng lặp for rất chậm nên ta phải vector hóa nó. Các training example có thể cho vào 1 matrix như đã nói ở phần 1 $X =\begin{bmatrix}{{\vert\atop x^{(1)}}\atop\vert}{{\vert\atop x^{(2)}}\atop\vert} \cdots {{\vert\atop x^{(m)}}\atop\vert} \end{bmatrix} $ Vector hóa của vòng lặp ở trên sẽ thành như sau $Z^{[1]} = W^{[1]}X + b^{[1]}$
$A^{[1]} = \sigma(Z^{[1]})$ $Z^{[2]} = W^{[2]}A^{[1]} + b^{[2]}$ $A^{[2]} = \sigma(Z^{[2]})$ Trong đó $Z^{[1]}$ là matrix có được khi xếp các vector z của layer 1 của mỗi training example vào mỗi cột $Z^{[1]} =\begin{bmatrix}{{\vert\atop z^{1}}\atop\vert}{{\vert\atop z^{1}}\atop\vert} \cdots {{\vert\atop z^{1}}\atop\vert} \end{bmatrix} $ Số ở ngoặc vuông biểu diễn index của layer, số trong ngoặc tròn thể hiện training example thứ mấy. Ví dụ giá trị góc trên cùng bên trái của $Z^{[1]}$ là pre-activation của neural thứ 1 của lớp thứ 1 của training example thứ 1 Tương tự $A^{ [1]}$ là matrix khi xếp các vector a của layer 1 của mỗi training example vào mỗi cột $A^{[1]} =\begin{bmatrix}{{\vert\atop a^{1}}\atop\vert}{{\vert\atop a^{1}}\atop\vert} \cdots {{\vert\atop a^{1}}\atop\vert} \end{bmatrix} $

Tham khảo

• Coursera deep learning
• Hugo Larochelle Neural Network