I. Deep L-layers neural network

Phần trước tôi đã trình bày biểu diễn của mạng neural với 2 lớp, ở phần này tôi sẽ trình bày tiếp mạng neural với nhiều lớp 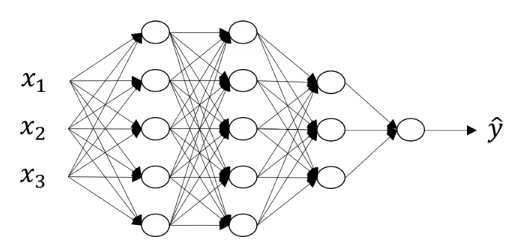Trên là ví dụ cho mạng neural có 4 lớp (ta không đếm lớp input) . Tổng quát hóa cho mạng có L lớp ta có các ký hiệu sau

• L: số lớp, ở ví dụ trên L = 4
• $n^{[l]}$: số node ở lớp l trong đó ta đánh số từ lớp input có l = 0. Ví dụ trên thì $n^{[1]} = 5$, $n^{[2]} = 5$, $n^{[L]} = $ số node ở lớp output $= 1$
• $a^{[l]}$: activation vector ở lớp thứ n $a^{[l]} = g(z^{[l]})$, $a^{[0]} = x$ (vector input), $a^{[L]} = \hat y $
• $w^{[l]}$: weight matrix để chuyển từ $z^{[l - 1]}$ tới $z^{[l]}$
• $b^{[l]}$ bias vector để chuyển từ $z^{[l - 1]}$ tới $z^{[l]}$

II. Neural network for multi-class classification

Các bài trước đã trình bày binary classification phân loại có hay không, phần này sẽ trình bày multi-class classification, một loại phân loại phổ quát hơn. 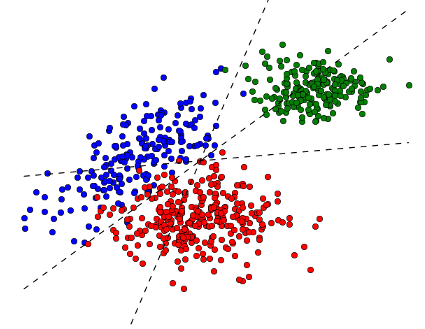Multi-class classification là từ input ta phân loại ra n class khác nhau. Ví dụ input là một matrix chứa các pixel của một bức ảnh, ta phân loại bức ảnh đó theo 1 loại trong số: ảnh chó, ảnh người, ảnh mèo, ảnh ô tô, ảnh xe đạp. Muốn vậy ở lớp output ta sẽ có n node mà mỗi node biểu hiện xác suất của loại c nếu ta biết được input x: $p(y = c|x)$ Khi ấy hàm softmax rất thích hợp để sử dụng như là activation function ở output layer

$o(a) = softmax(a) = \begin{bmatrix}\frac{exp(a_1)}{\sum_{i}exp(a_i)} & ... & \frac{exp(a_C)}{\sum_{i}exp(a_i)} \end{bmatrix}^\intercal$

Trông có vẻ phức tạp nhưng ta hãy phân tích một chút

• Input là 1 vector, output cũng là 1 vector
• Phần tử thứ nhất: tử số là $e$ mũ số thứ nhất của vector cũ, mẫu số là tổng của $e$ mũ của tất cả các phần tử của vector cũ. Các phần tử tiếp theo cũng tương tự

Hàm softmax thích hợp để biểu diễn xác suất của mỗi class vì

• Các phần tử đều $>0$ và $\leq1$
• Tổng của tất cả phẩn tử $= 1$

Ví dụ ở bài toán phân loại ảnh chó, ảnh người, ảnh mèo, ảnh ô tô, ảnh xe đạp ở trên, sau khi áp dụng softmax ở output layer ta có vector $\begin{bmatrix}0.8&0.05&0.05&0.05&0.05\end{bmatrix}^\intercal$ Ta biết xác suất là ảnh chó là 0.8, là ảnh người là 0.05... Do đó ta có thể kết luận là ảnh chó vì có xác xuất lớn hơn các loại còn lại.

III. Forward propagation in a deep network

Thực hiện việc tính toán với từng hidden layer $\rightarrow$ output layer tương tự như với mạng neural có 2 lớp.

• Với hidden layer thứ nhất: $z^{[1]} = W^{[1]}a^{[0]} + b^{[1]} \quad (a^{[0]} = x)$
  $a^{[1]} = g(z^{[1]})$

• Hidden layer thứ hai: $z^{[2]} = W^{[2]}a^{[1]} + b^{[2]}$
  $a^{[2]} = g(z^{[2]})$

• Tổng quát hóa cho layer n: $z^{[l]} = W^{[l]}a^{[l - 1]} + b^{[l]}$
  $a^{[l]} = g(z^{[l]})$

• Thực hiện vector hóa cho tất cả các training example for l = 1..L $Z^{[l]} = W^{[l]}A^{[l - 1]} + b^{[l]}$
  $A^{[l]} = g(Z^{[l]})$

  Trong đó $A^{[0]} = X$ là matrix các training example xếp thành cột như đã nói ở phần trước $Z^{[l]}$ là matrix có được khi xếp các vector z của layer 1 của mỗi training example vào mỗi cột $Z^{[l]} =\begin{bmatrix}{{\vert\atop z^{l}}\atop\vert}{{\vert\atop z^{l}}\atop\vert} \cdots {{\vert\atop z^{l}}\atop\vert} \end{bmatrix} $ VD: $z^{[1](1)}$ là vector biểu diễn các node ở layer 1 của training example thứ nhất g là activation function có thể là 1 trong các hàm đã nói ở phần 1. Riêng ở output layer đối với binary classification thì g sẽ dùng hàm sigmoid, còn với multi-class classification ta dùng hàm softmax.

IV. Intuition for deep network

Có thể hình dung là để nhận diện được mặt người thì mạng neural nhiều lớp sẽ nhận dạng các đặc điểm đơn giản ở các lớp đầu, sau đó ở các lớp sau sẽ dần dần nhận dạng được các feature phức tạp hơn 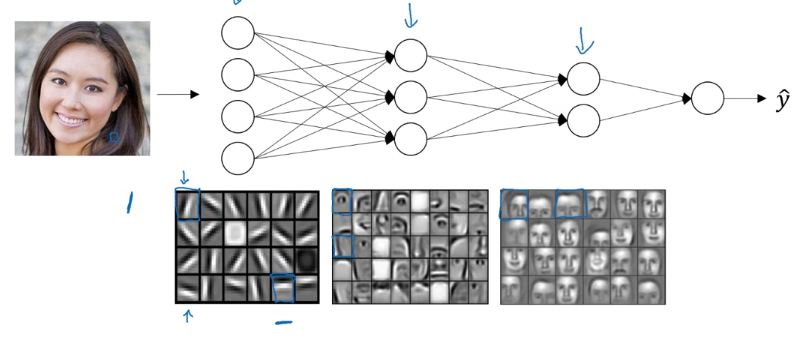Ví dụ ở hidden layer thứ nhất sẽ nhận dạng các cạnh, từ các cạnh đó sẽ ở layer tiếp theo sẽ nhận dạng được mắt, mũi, tai. Layer cuối cùng có thể nhận dạng được cả khuôn mặt

Như đã trình bày phần forward propagation với mỗi lớp, ta đều có các parameter $W^{[l]}$ và $b^{[l]}$ tương ứng. Từ input x thực hiện forward propagation qua mỗi lớp ta áp dụng các parameter này và đến cuối cùng tính ra giá trị dự đoán $\hat y$. Hình dung rằng ta được cung cấp khoảng 1 triệu training example x như vậy, làm thế nào để optimize các parameter các parameter $W^{[l]}$ và $b^{[l]}$ để output gần đúng với nhiều nhất các example và mong rằng nó sẽ dự đoán tốt khi dùng với input khác ngoài tập các training input. Để thực hiện điều đó, sau đây tôi sẽ trình bày thuật toán gradient descent. Câu hỏi đặt ra đầu tiên là làm sao để có thể đo được sự gần đúng của output của mạng neural và dữ liệu thực tế, loss function sẽ cho ta câu trả lời.

V. Loss function

Phần này sẽ trình bày loss function cho multi-class classification. Giả sử ta biết được input x và output y = c với training example t nào đó. Ta muốn maximize xác suất mà mạng neural dự đoán cho y = c sẽ là giá trị của node thứ c ở output layer (xem thêm ở mục 2). Do đó ta muốn maximize

$\sum_{c}1_(y=c)f(x)_c$ Trong đó 1(y=c) trả về 1 nếu y = c và trả về 0 nếu y khác c $f(x)$ là vector output của mạng neural, $f(x)_c$ là giá trị của node thứ c Ta tổng tất cả các node của output layer nhưng chỉ giữ lại giá trị của node dự đoán đúng class với y từ training data. Vì $log$ là hàm tăng đồng nhất nên thay vì maximize một hàm ta có thể minimize -$log$ của hàm đó. Do đó ta muốn minimize -$\sum_{c}1_(y=c)logf(x)_c$ Hàm trên ta gọi là loss function. Minimize hàm đó tức là ta muốn loss function là nhỏ nhất.

Tham khảo

• Coursera deep learning
• Hugo Larochelle Neural Network