Bài trước tôi đã trình bày các công thức của back propagation trong bài này tôi sẽ chứng minh các công thức đó

I. Proof d\mathbf{z}^{[L]} = \hat \mathbf{y} - \mathbf{y}

Trước hết ta chứng minh cho trường hợp chỉ 1 training example. Ta sẽ tính đạo hàm riêng đối với $z^{[L]}_c$ (phần từ thứ c của output z, sau khi áp dụng hàm softmax) của hàm loss là $-logf(x)_y$ (đọc thêm ở bài 3, phân biệt y viết thường và $\mathbf{y}$ viết đậm: y là số thứ tự của phần tử mà vector $\mathbf{y}$ có giá trị là 1). Trông các bước có vẻ phức tạp nhưng nếu theo dõi từng bước một bạn sẽ thấy cũng khá dễ hiểu và đẹp.

$\dfrac{\partial-logf(x)_y}{\partial z^{[L]}_c} = \dfrac{\partial -log(softmax(z^{[L]})_y)}{\partial z^{[L]}_c}$

$\qquad\qquad \qquad=\dfrac{\partial -log(\dfrac{e^{z^{[L]}_y}}{\sum_i{e^{z^{[L]}_i}}})}{\partial z^{[L]}_c}$

$\qquad\qquad \qquad= -\dfrac{\sum_i{e^{z^{[L]}_i}}}{e^{z^{[L]}_y}} \dfrac{\partial \dfrac{e^{z^{[L]}_y}}{\sum_i{e^{z^{[L]}_i}}}}{\partial z^{[L]}_c}$

Đến đây để tính đạo hàm riêng của $\dfrac{\partial \dfrac{e^{z^{[L]}_y}}{\sum_i{e^{z^{[L]}_i}}}}{\partial z^{[L]}_c}$ ta áp dụng quy tắc tìm đạo hàm riêng của $\dfrac{g(x)}{h(x)}$

$\qquad\qquad\qquad\qquad\dfrac{\partial\dfrac{g(x)}{h(x)}}{\partial x}=\dfrac{\partial g(x)}{\partial x} \dfrac{1}{h(x)} - \dfrac{g(x)}{h^2(x)}\dfrac{\partial h(x)}{\partial x}$

Nên ta có

$\dfrac{\partial-logf(x)_y}{\partial z^{[L]}_c} = -\dfrac{\sum_i{e^{z^{[L]}_i}}}{e^{z^{[L]}_y}} (\dfrac{\partial e^{z^{[L]}_y}}{\partial z^{[L]}_c }\dfrac{1}{\sum_i{e^{z^{[L]}_i}}} - \dfrac{e^{z^{[L]}_y}}{\sum_i{e^{z^{[L]}_i}} \sum_i{e^{z^{[L]}_i}}} \dfrac{\partial \sum_i{e^{z^{[L]}_i}}}{\partial z^{[L]}_c})$

$\qquad\qquad \qquad=-\dfrac{\sum_i{e^{z^{[L]}_i}}}{e^{z^{[L]}_y}} (1_{(c = y)}e^{z^{[L]}_c}\dfrac{1}{\sum_i{e^{z^{[L]}_i}}} - \dfrac{e^{z^{[L]}_y}}{\sum_i{e^{z^{[L]}_i}} \sum_i{e^{z^{[L]}_i}}} e^{z^{[L]}_c}$ $\qquad\mathbb1_{(c = y)}$ là hàm indicator trả về 1 nếu c $=$ y và trả về 0 nếu y $\ne$ c

$\qquad\qquad \qquad=-\dfrac{\sum_i{e^{z^{[L]}_i}}}{e^{z^{[L]}_y}} (1_{(c = y)}\dfrac{e^{z^{[L]}_c}}{\sum_i{e^{z^{[L]}_i}}} - \dfrac{e^{z^{[L]}_y}}{\sum_i{e^{z^{[L]}_i}}} \dfrac{e^{z^{[L]}_c}}{\sum_i{e^{z^{[L]}_i}}}$

$\qquad\qquad \qquad=-\dfrac{1}{softmax(z^{[L]})_y} (1_{(c = y)}softmax(z^{[L]})_c - softmax(z^{[L]})_ysoftmax(z^{[L]})_c)$

$\qquad\qquad \qquad= -(1_{(c = y)} - softmax(z^{[L]})_c)$

$\qquad\qquad \qquad= -(1_{(c = y)} - \hat y_c)$

$\qquad\qquad \qquad= \hat y_c - 1_{(c = y)}$

Do đó nếu đạo hàm riêng cả vector $z^{[L]}$ thì

$\dfrac{\partial-logf(x)_y}{\partial \mathbf{z^{[L]}}} = \mathbf{\hat y} - \mathbf{y} \qquad$ hay \qquad d\mathbf{z}^{[L]} = \hat \mathbf{y} - \mathbf{y}

---

II. Proof $d\mathbf a^{[l-1]} = W^{[l]T} d\mathbf z^{[l]}$

Giả sử ta đã tính được đạo hàm riêng của $\mathbf z$ ở lớp thứ $l$ làm sao ta có thể tính tiếp đạo hàm riêng $\mathbf a$ ở lớp $l - 1$? Ta nhắc lại phần tử thứ i của $\mathbf z^{[l]}$ được tính từ $\mathbf a^{[l - 1]}$ như sau

$\mathbf z^{[l]}_i = \sum_j{W^{[l]}_{i,j}} \mathbf a^{[l - 1]}_j + \mathbf b^{[l]}_i \qquad$ (Tích vector của row thứ i của matrix $W^{[l]}$ và vector $\mathbf a^{[l - 1]} +$ phần tử thứ i của vector bias $b^{[l]}$)

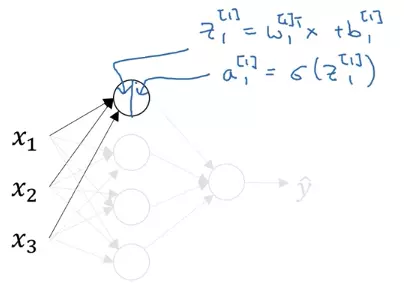$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad$(Trong ảnh thay x bằng a)

Ta thấy mỗi phần từ $\mathbf a^{[l - 1]}_j$ đều đóng vai trò vào việc tính toán từng phần tử $\mathbf z^{[l]}_i$ mà ta biết hàm loss function là hàm số của $\mathbf z^{[l]}$, đã biết được đạo hàm riêng của $\mathbf z^{[l]}$, điều đó gợi ý ta sử dụng chain rule

Chain rule Nếu hàm số $f(a)$ là hàm số của các hàm số $g_i(a)$ thì $\dfrac{\partial f(a)}{\partial a} = \sum_i{\dfrac{\partial f(a)}{\partial g_i(a)}\dfrac{\partial g_i(a)}{\partial a}}$

Dùng chain rule ta set $f(a)$ là loss function $-logf(x)_y$, $g_i(a)$ là $\mathbf z^{[l]}_i$ còn a là $\mathbf a^{[l - 1]}_c$, ta tính đạo hàm riêng đối với phần tử thứ c của $\mathbf a^{[l - 1]}$

$\dfrac{\partial-logf(x)_y}{\partial \mathbf a^{[l - 1]}_c} = \sum_i{\dfrac{\partial-logf(x)_y}{\partial \mathbf z^{[l]}_i} \dfrac{\partial \mathbf z^{[l]}_i}{\partial \mathbf a^{[l - 1]}_c}} \qquad (1)$

Do $\mathbf z^{[l]}_i = \sum_j{W^{[l]}_{i,j}} \mathbf a^{[l - 1]}_j + b^{[l]}_i$ nên $\dfrac{\partial \mathbf z^{[l]}_i}{\partial \mathbf a^{[l - 1]}_c} = W^{[l]}_{i, c}$ thay vào $(1)$

$\dfrac{\partial-logf(x)_y}{\partial \mathbf a^{[l - 1]}_c} = \sum_i{\dfrac{\partial-logf(x)_y}{\partial \mathbf z^{[l]}_i} W^{[l]}_{i, c}}$ $\qquad\qquad\qquad=$ Tích của vector $d\mathbf z^{[l]}$ và cột thứ i của matrix $W^{[l]}$

Do đó nếu đạo hàm riêng cả vector $\mathbf a^{[l - 1]}$ thì

$\dfrac{\partial-logf(x)_y}{\partial \mathbf a^{[l - 1]}} = W^{[l]T} \dfrac{\partial-logf(x)_y}{\partial \mathbf z^{[l]}}\qquad$ hay $\qquad d\mathbf a^{[l-1]} = W^{[l]T} d\mathbf z^{[l]}$

---

III. Proof $dW^{[l]} = d\mathbf z^{[l]} \mathbf a^{[l - 1]T} $

Như đã nói ở phần trên, công thức liên hệ giữa lớp $l - 1$ và lớp $l$ là

$\mathbf z^{[l]}_i = \sum_j{W^{[l]}_{i,j}} \mathbf a^{[l - 1]}_j + \mathbf b^{[l]}_i \qquad$

Để ý thấy $W^{[l]}_{i,j}$ chỉ đóng góp cho biểu thức của $\mathbf z^{[l]}_i$ mà không xuất hiện trong các phẩn tử khác của $\mathbf z^{[l]}$, ta áp dụng chain rule để tính đạo hàm riêng của cost function đối với $W^{[l]}_{i,j}$

$\dfrac{\partial-logf(x)y}{\partial W^{[l]}{i,j}} = \dfrac{\partial-logf(x)_y}{\partial \mathbf z^{[l]}_i} \dfrac{\partial \mathbf z^{[l]}i}{\partial W^{[l]}{i,j}} $

$\qquad\qquad\qquad = \dfrac{\partial-logf(x)_y}{\partial \mathbf z^{[l]}_i} \mathbf a^{[l - 1]}_j$

Do đó nếu đạo hàm riêng cả matrix $W^{[l]}$ thì

$\dfrac{\partial-logf(x)_y}{\partial W^{[l]}} = \dfrac{\partial-logf(x)_y}{\partial \mathbf z^{[l]}}\mathbf a^{[l - 1]T}\qquad$ hay $\qquad dW^{[l]} = d\mathbf z^{[l]} \mathbf a^{[l - 1]T} \qquad$ (Phần tử thứ i, j của $W^{[l]}$ là $W^{[l]}_{i,j}$ bằng phần tử thứ i của $d\mathbf z^{[l]}$ nhân với phần tử thứ j của $\mathbf a^{[l - 1]}$)

---

IV. Proof $d\mathbf b^{[l]} = d\mathbf z^{[l]}$

Nhắc lại công thức liên hệ giữa lớp $l - 1$ và lớp $l$

$\mathbf z^{[l]}_i = \sum_j{W^{[l]}_{i,j}} \mathbf a^{[l - 1]}_j + \mathbf b^{[l]}_i \qquad$

$b^{[l]}_i$ chỉ đóng góp cho biểu thức của $z^{[l]}_i$ mà không xuất hiện trong các phẩn tử khác của $\mathbf z^{[l]}$, ta áp dụng chain rule để tính đạo hàm riêng của cost function đối với phần tử thứ i của $\mathbf b^{[l]}$

$\dfrac{\partial-logf(x)_y}{\partial \mathbf b^{[l]}_i} = \dfrac{\partial-logf(x)_y}{\partial \mathbf z^{[l]}_i} \dfrac{\partial \mathbf z^{[l]}_i}{\partial\mathbf b^{[l]}_i} $

$\qquad\qquad\qquad = \dfrac{\partial-logf(x)_y}{\partial \mathbf z^{[l]}_i} \times 1$

Do đó nếu đạo hàm riêng cả vector $\mathbf b^{[l]}$ thì

$\dfrac{\partial-logf(x)_y}{\partial\mathbf b^{[l]}} = \dfrac{\partial-logf(x)_y}{\partial \mathbf z^{[l]}}\qquad$ hay $d\mathbf b^{[l]} = d\mathbf z^{[l]}$

---

V Proof $d\mathbf z^{[l]} = d\mathbf a^{[l]} * g^{[l]'}(\mathbf z^{[l]})$

Trong lớp $l$ công thức liên hệ giữa $\mathbf z^{[l]}_i$ và $\mathbf a^{[l]}_i$ là

$\mathbf a^{[l]}_i = g^{[l]}(\mathbf z^{[l]}_i)\qquad$ trong đó $g^{[l]}()$ là hàm activation của lớp $l$

Áp dụng chain rule ta có

$\dfrac{\partial-logf(x)_y}{\partial \mathbf z^{[l]}_i} = \dfrac{\partial-logf(x)_y}{\partial \mathbf a^{[l]}_i} \dfrac{\partial \mathbf a^{[l]}_i}{\partial \mathbf z^{[l]}_i}$

$\qquad\qquad\qquad = \dfrac{\partial-logf(x)_y}{\partial \mathbf a^{[l]}_i}\dfrac{\partial g^{[l]}(\mathbf z^{[l]}_i)}{\partial \mathbf z^{[l]}_i}$ Tức là đạo hàm riêng đối với phần tử thứ i của $\mathbf z^{[l]}$ bằng đạo hàm riêng đối với phần tử thứ i của $\mathbf a^{[l]}$ nhân với đạo hàm riêng của hàm activation đối với phần tử thứ i của $\mathbf z^{[l]}$

Do đó nếu đạo hàm riêng cả vector $\mathbf z^{[l]}$ thì

$\dfrac{\partial-logf(x)_y}{\partial \mathbf z^{[l]}} = \dfrac{\partial-logf(x)_y}{\partial \mathbf a^{[l]}} * (elementwise)\dfrac{\partial g^{[l]}(\mathbf z^{[l]})}{\partial \mathbf z^{[l]}}\qquad$ hay $\qquad d\mathbf z^{[l]} = d\mathbf a^{[l]} * g^{[l]'}(\mathbf z^{[l]})$ (nhân 2 phần từ tương ứng của 2 vector $d\mathbf a^{[l]}$ và $g^{[l]'}(\mathbf z^{[l]})$ với nhau để ra vector $d\mathbf z^{[l]}$)

---

Tham khảo

• Coursera deep learning
• Hugo Larochelle Neural Network