Lý thuyết xác suất (P2)
Bài đăng này đã không được cập nhật trong 4 năm
I. Sự kiện độc lập
1. Góc nhìn trực quan
Hai sự kiện độc lập với nhau nếu biết trước một sự kiện sẽ xảy ra không ảnh hưởng tới niềm tin của chúng ta về khả năng sẽ xảy ra sự kiện kia.
P(B|A) = P(B)
Ví dụ:
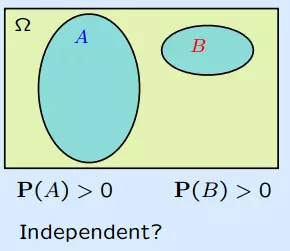 Hai sự kiện A và B không giao nhau thoạt nhìn có vẻ độc lập. Nhưng nếu biết một sự kiện sẽ xảy ra thì có thể kết luận luôn là sự kiện kia không thể xảy ra nên có thể nói 2 sự kiện này "rất phụ thuộc" vào nhau.
Hai sự kiện A và B không giao nhau thoạt nhìn có vẻ độc lập. Nhưng nếu biết một sự kiện sẽ xảy ra thì có thể kết luận luôn là sự kiện kia không thể xảy ra nên có thể nói 2 sự kiện này "rất phụ thuộc" vào nhau.
2. Định nghĩa
Hai sự kiện gọi là độc lập vơi nhau nếu và chỉ nếu:
P(A∩B) = P(A)P(B)
Từ định nghĩa trên nếu P(A) ≠ 0 thì:
P(A∩B) = P(A)P(B|A) = P(A)P(B)
nên ta có
P(B|A) = P(B)
hơn nữa trường hợp P(A) = 0 thì công thức trên cũng áp dụng được
3.Tính độc lập của sự kiện bù nhau
Nếu A và B độc lập với nhau thì A và B' (sự kiện bù của B) cũng độc lập với nhau
 Chứng minh:
Ta có:
Chứng minh:
Ta có:
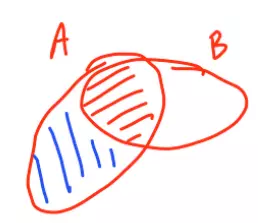
A = (A∩B) ∪ (A∩B')
(A∩B là sự kiện được gạch đỏ, A∩B' là sự kiện gạch xanh)
Do 2 sự kiện này không giao nhau nên:
P(A) = P(A∩B) + P(A∩B') = P(A)P(B) + P(A∩B')
Do đó
P(A∩B') = P(A) - P(A)P(B) = P(A)(1 - P(B)) = P(A)P(B')
4. Độc lập có điều kiện
Nếu ta biết được sự kiện C xảy ra thì A và B có độc lập với nhau?
Định nghĩa: 2 sự kiện A và B độc lập với nhau nếu ta biết C xảy ra nếu và chỉ nếu
P(A∩B|C) = P(A|C)P(B|C)
Ví dụ:
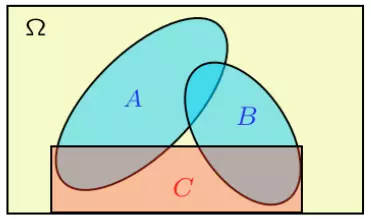 Nếu biết C sẽ xảy ra thì vì A và B không giao nhau. Như ví dụ ở mục 1 ta có thể kết luận là 2 sự kiện này không độc lập với nhau
Hai sự kiện trở nên thể độc lập hay không độc lập với nhau nếu biết một sự kiện xảy ra.
Ví dụ ta có bài toán sau:
Nếu biết C sẽ xảy ra thì vì A và B không giao nhau. Như ví dụ ở mục 1 ta có thể kết luận là 2 sự kiện này không độc lập với nhau
Hai sự kiện trở nên thể độc lập hay không độc lập với nhau nếu biết một sự kiện xảy ra.
Ví dụ ta có bài toán sau:
- Có 2 đồng xu không đều A và B (xác suất sấp, ngửa không là 50:50). Trong đó P(H | xu được chọn là A) = 0.9, P(H | xu được chọn là B) = 0.1
- Trước khi tung xu ta chọn 1 trong 2 đồng xu ngẫu nhiên Nếu biết trước được A hay B được chọn thì các lần tung đồng xu là độc lập nhau. Trong trường hợp chưa biết trước: P(lần tung 11 = H) = P(A)P(lần tung 11 = H | A) + P(B)P(lần tung 11 = H | B) = 0.5 x 0.9 + 0.5 x 0.1 = 0.5 Nếu ai đó nói cho ta biết cả 10 lần tung trước đều là H thì: P(lần tung 11 = H | cả 10 lần tung trước đều là H) ≈ P(lần tung 11 = H | xu được chọn là A) vì ta có thể gần như chắc chắn xu được chọn là A nếu cả 10 lần tung đều ra H =0.9 khác với 0.5 ở trường hợp trên. Vậy có thể nói là lần tung thứ 11 có phụ thuộc vào 10 lần tung trước.
5.Độc lập của nhiều sự kiện
Trực quan mà nói thì nhiều sự kiện được gọi là độc lập với nhau nếu biết thông tin một vài sự kiện không làm thay đổi xác suất của các sự kiện khác VD: nếu các sự kiện A1, A2, ... độc lập với nhau thì: P(A3∩A4') = P(A3∩A4' | A1∪(A2∩A5')) P(A3) = P(A3|A1∩A2) = P(A3|A1∩A2') = P(A3|A1'∩A2)
Định nghĩa:
Các các sự kiện A1, A2, ..., An độc lập với nhau nếu và chỉ nếu:
P(Ai ∩ Aj ∩ ··· ∩ Am) = P(Ai)P(Aj) ··· P(Am) với mọi các chỉ số i, j, ..., m khác nhau
Nếu các sự kiện độc lập với nhau theo cặp thì chưa chắc chúng đã độc lập với nhau Ví dụ ta xét bài toán sau:
- Tung 2 lần 1 đồng xu đều độc lập với nhau
- H1: lần tung đầu là H
- H2: lần tung thứ hai là H
- P(H1) = P(H2) = 0.5
- C là sự kiện 2 lần tung giống nhau {HH, TT}
Ta có H1 và C độc lập với nhau vì: P(H1∩C) = P(H1∩H2) = 1/4 và P(H1)P(C) = 1/2 x 1/2 = 1/4 Tương tự ta cũng có H2 và C cũng độc lập với nhau Còn H1 và H2 độc lập với nhau như đã nói
Nhưng H1, H2, C không độc lập vì: P(H1∩H2∩C) = P(HH) = 1/4. Mà P(H1)P(H2)P(C) = 1/8 Hay: P(C|H1∩H2) = 1 ≠ P(C) = 1/2 (Thông tin về H1, H2 thay đổi xác suất của C)
6.Ví dụ độ tin cậy của hệ thống
Giả sử ta có các unit như hình vẽ.
Gọi U1, ..., Un là sự kiện unit thứ i "up". Các sự kiện này độc lập với nhau. Và gọi P(U1) = p1, P(U2) = p2, ...
Gọi F1, ..., Fn là sự kiện unit thứ i "down". Các sự kiện này độc lập với nhau
Trường hợp các unit mắc nối tiếp nhau
 P(hệ thống "up") = P(U1∩U2∩U3) = P(U1)P(U2)P(U3) = p1p2p3
P(hệ thống "up") = P(U1∩U2∩U3) = P(U1)P(U2)P(U3) = p1p2p3
Trường hợp các unit mắc song song với nhau
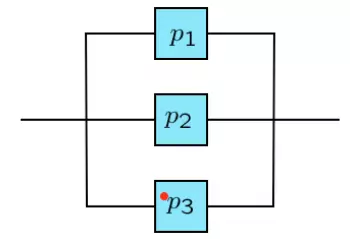 P(hệ thống "up") = P(U1∪U2∪U3) = 1 - P(F1∩F2∩F3) = 1 - P(F1)P(F2)P(F3) = 1 - (1 - p1)(1 - p2)(1 - p3)
P(hệ thống "up") = P(U1∪U2∪U3) = 1 - P(F1∩F2∩F3) = 1 - P(F1)P(F2)P(F3) = 1 - (1 - p1)(1 - p2)(1 - p3)
II.Tham khảo
- MITx: 6.041x Introduction to Probability - The Science of Uncertainty
All rights reserved