Neural Network Fundamental 1: Intuition and Notation
Bài đăng này đã không được cập nhật trong 4 năm
I. Neural Network Intuition
Gần đây neural network, deep learning nổi lên như là một trend rất hot trong kỷ nguyên của trí tuệ nhân tạo. Vậy neural network là gì và tại sao nó lại có thể hoạt động? Để hiểu một cách intuition về neural network chúng ta hãy xem xét bài toán sau đây.
Giả sử ta có một dataset về các căn nhà chứa các thông số như là size, #bedroom, zip code, wealth, price và dựa vào data có sẵn chúng ta muốn dự đoán price của các căn nhà mới. Nói cách khác chúng ta muốn xây dựng một hàm số để có thể map input (size, #bedroom ...) với price.
Ví dụ xử lý bài toán trên với Neural network:
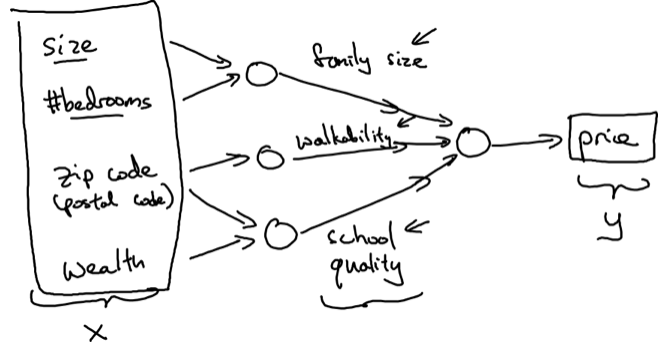 Neural network được tổ chức theo các lớp, mỗi lớp chứa các neural. Mỗi neural sẽ tính toán một giá trị mới dựa vào giá trị của các neural của lớp trước đó.
Như trên hình ta thấy lớp đầu tiên là lớp input. Lớp thứ 2 chứa các neural là sự kết hợp của các input. Ví dụ từ size và #bedrooms, ta có thể estimate được family size, từ zip code xác định được walkability, từ zip code và wealth estimate được school quality. Ở lớp tiếp theo thì kết hợp family size, walkability, school quality ta có thể dự đoán được price của căn nhà đó.
Cứ như vậy, giả sử một neural network có rất nhiều lớp, thì lớp tiếp theo chứa các neural là sự kết hợp của các neural ở lớp trước đó, cho ta một cái nhìn về một feature tổng quát hơn, và rồi cuối cùng ta có thể predict được giá trị ở lớp cuối cùng.
Neural network được tổ chức theo các lớp, mỗi lớp chứa các neural. Mỗi neural sẽ tính toán một giá trị mới dựa vào giá trị của các neural của lớp trước đó.
Như trên hình ta thấy lớp đầu tiên là lớp input. Lớp thứ 2 chứa các neural là sự kết hợp của các input. Ví dụ từ size và #bedrooms, ta có thể estimate được family size, từ zip code xác định được walkability, từ zip code và wealth estimate được school quality. Ở lớp tiếp theo thì kết hợp family size, walkability, school quality ta có thể dự đoán được price của căn nhà đó.
Cứ như vậy, giả sử một neural network có rất nhiều lớp, thì lớp tiếp theo chứa các neural là sự kết hợp của các neural ở lớp trước đó, cho ta một cái nhìn về một feature tổng quát hơn, và rồi cuối cùng ta có thể predict được giá trị ở lớp cuối cùng.
II. Some Notation
Chúng ta hãy cùng xem xét bài toán phân loại nhị phân nhận dạng một bức ảnh có phải là ảnh con mèo hay không.
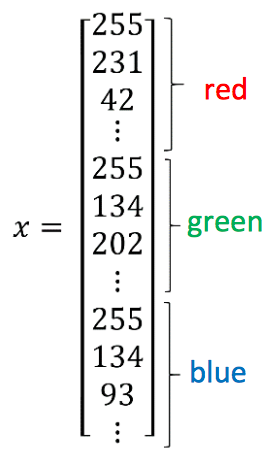
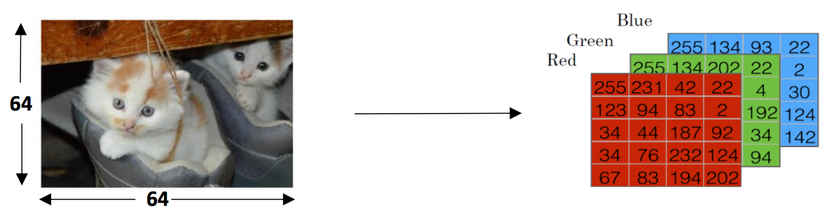 Ảnh được lưu trữ trong máy tính bằng 3 ma trận kích thước 64x64 tương ứng với 3 màu: red, blue, green. Thay vì sử dụng 3 ma trận riêng biệt ta sẽ gộp chúng lại để tạo ra feature vector x với kích thước trong đó
Ảnh được lưu trữ trong máy tính bằng 3 ma trận kích thước 64x64 tương ứng với 3 màu: red, blue, green. Thay vì sử dụng 3 ma trận riêng biệt ta sẽ gộp chúng lại để tạo ra feature vector x với kích thước trong đó
 Ký hiệu:
: Feature vector (như ví dụ trên là các pixel của ảnh xếp thành 1 column vector)
: Output label (bức ảnh đó có phải là mèo không)
: Một training example (input của neural network, chúng ta biết được cả và )
: Số lượng training example
: Tập hợp m training examples:
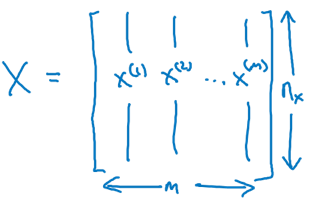
: Input matrix, các cột là các feature vector. Có m cột tương ứng với training example thứ 1 đến thứ m
Ký hiệu:
: Feature vector (như ví dụ trên là các pixel của ảnh xếp thành 1 column vector)
: Output label (bức ảnh đó có phải là mèo không)
: Một training example (input của neural network, chúng ta biết được cả và )
: Số lượng training example
: Tập hợp m training examples:
: Input matrix, các cột là các feature vector. Có m cột tương ứng với training example thứ 1 đến thứ m
 : Output row vector chứa các label của training example từ 1 tới m
: Output row vector chứa các label của training example từ 1 tới m
III. Artificial Neural
Trước khi chuyển tới mạng neural, hãy cùng xem một neural làm những gì
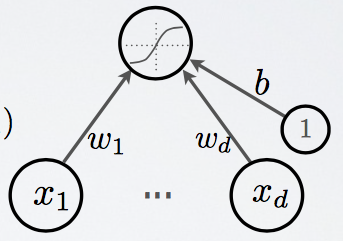 Neural ở trên đọc vector input x, thực hiện tính toán quyết định giá trị của nó lấy "nhiều" hay "ít" các giá trị , , ...
Việc tính toán được thực hiện qua 2 bước
Neural ở trên đọc vector input x, thực hiện tính toán quyết định giá trị của nó lấy "nhiều" hay "ít" các giá trị , , ...
Việc tính toán được thực hiện qua 2 bước
- Tính pre-activation của neural : vector chứa các weight kết nối input và với neural : neural bias
- Neural activation Áp dụng một hàm activation (sẽ nói ở phần sau) vào giá trị z là hàm activation
IV. Activation Function
Sigmoid function
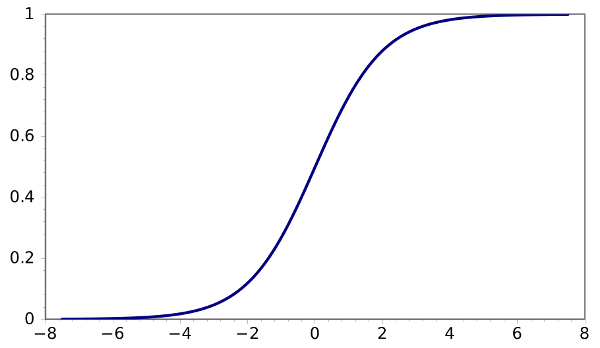
- Output trong khoảng từ 0 tới 1
- Luôn > 0
- Là hàm tăng
Vì hàm sigmoid output trong khoảng từ 0 tới 1 nên hay được dùng cho lớp cuối cùng của mạng neural, ví dụ nếu output 0.5 sẽ đoán label là 1, output 0.5 đoán label là 0. Với các neural không thuộc ở lớp cuối cùng của mạng neural người ta không dùng hàm sigmoid vì hàm gần như luôn luôn tốt hơn.
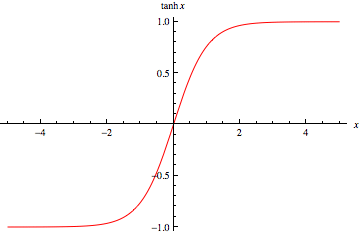
- Output trong khoảng từ -1 tới 1
- Là hàm tăng Lý do hàm gần như luôn luôn tốt hơn sigmoid cho các lớp ở giữa của mạng neural là vì nó làm cho các giá trị ở một lớp có mean là 0 thay vì 0.5 như hàm sigmoid Điểm yếu của cả hàm sigmoid và đó là khi z có giá trị rất lớn hoặc rất nhỏ thì đạo hàm tiến gần tới 0, điều đó có thể dẫn tới việc làm chậm đi thuật toán gradient descent sẽ nói đến ở sau. Chính vì điều này nên hàm ReLu trở nên phổ biến.
ReLu
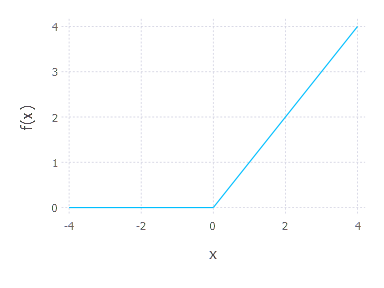
- Bị chặn dưới bởi 0
- Không bị chặn trên
- Là hàm tăng
Hàm ReLu ngày càng được sử dụng phổ biến như một hàm activation default trong neural network
Tham khảo
- Coursera deep learning
- Hugo Larochelle Neural Network
All rights reserved