18.7K 1.2K 37

Đã đăng vào thg 5 11, 2018 7:54 SA

trong

19 phút đọc

8.5K

Bài toán các vị tướng Byzantine và ứng dụng trong Blockchain

Editors' Choice

Bài đăng này đã không được cập nhật trong 6 năm

Lời nói đầu

Dân IT đúng là khổ. Chạy theo công nghệ thật là mệt.

Ở thế giới hiện tại công nghệ phát triển như vũ bão, hot trend thay đổi không ngừng, chỉ một thời gian dừng chân đứng lại thôi là bạn có thể bị bỏ rơi ngay. =))

Xuất thân từ một PHP Developer, mình đã từng trải qua các quãng thời gian tìm hiểu về nào là Laravel Framework, rồi ReactJS, cho đến Docker, DevOps ... mỗi thứ mới chỉ biết được một ít mà đã phải nhảy sang cái khác.

Thời gian gần đây thì thấy mọi người ai ai cũng bàn tán về Blockchain, đâu đâu cũng thấy Blockchain, nên mình cũng có dành chút thời gian tìm hiểu xem nó là cái gì mà sao lại hot như vậy Mong là có đủ kiến thức để viết lại thành một series về Blockchain trên Viblo

Hy vọng có thể nhận được sự chú ý và ủng hộ từ mọi người.

Các bài viết có thể không theo một mạch nhất định, mình sẽ cố gắng sắp xếp lại theo thứ tự tại series Mastering Blockchain sau.

Còn ở bài đầu tiên này, mình xin được giới thiệu về một bài toán khá là thú vị, mà cũng có ít nhiều liên quan đến Blockchain. Mình tình cờ biết đến nó khi tìm hiểu về thuật toán Proof of Stake của Ethereum. Có lẽ một chút hiểu biết nhất định về vấn đề này sẽ giúp bạn dễ dàng theo dõi hơn những phần tiếp theo trong series Mastering Blockchain

Bài toán 2 vị tướng quân

Bài toán 2 vị tướng quân (2 generals problem) là một bài toán của khoa học máy tính, được đưa ra như một vấn đề, một thách thức cần giải quyết, nhằm đạt được một thoả thuận thông qua việc trao đổi thông tin trong một môi trường không đáng tin cậy. Nó thường được đưa ra trong những bài học nhập môn về Computer Networking, trình bày và giải thích tại sao giao thức TCP không thể đảm bảo được sự nhất quán (consistency) giữa các điểm kết nối.

Nhìn chung, bài toán 2 vị tướng quân nói rằng: trong một môi trường mà vấn đề trao đổi (communication) có thể xảy ra lỗi thì không thể đảm bảo được sự thống nhất giữa 2 bên.

Nội dung của bài toán 2 vị tướng quân có thể được miêu tả như sau:

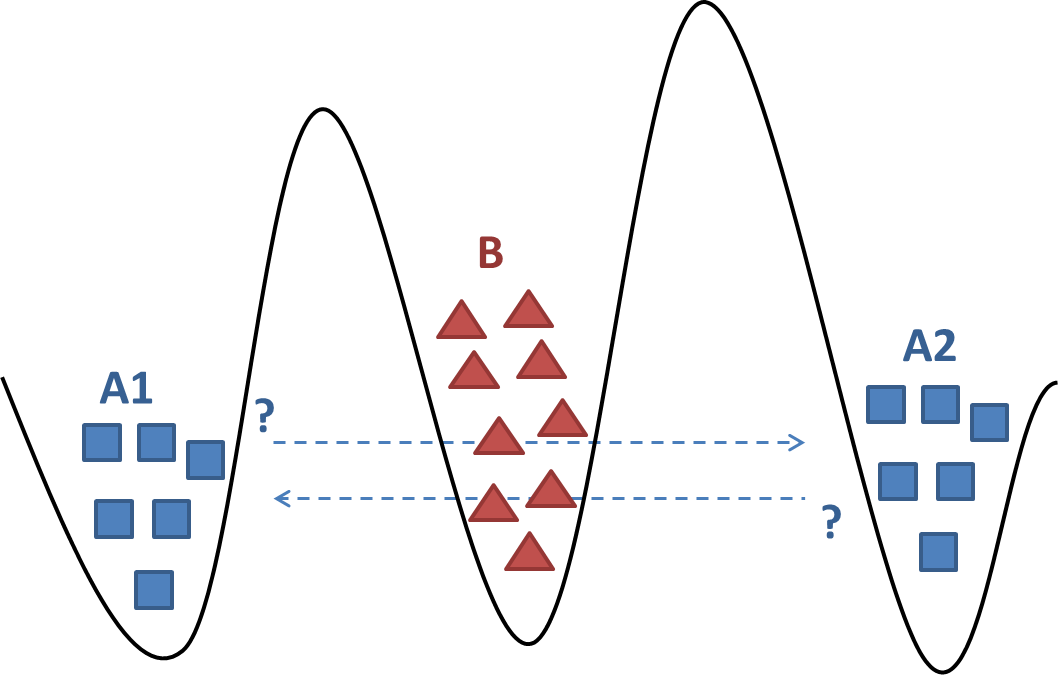
2 generals problem

2 đội quân được lãnh đạo bởi 2 vị tướng A1 và A2, cùng tấn công một thành phố B nằm ở giữa.
Hai vị tướng A1 và A2 chỉ có thể trao đổi thông qua việc gửi thư cho nhau, nhưng xảy ra một vấn đề là người đưa thư cần phải đi qua thành phố B, dẫn đến việc hoàn toàn có khả năng người đưa thư bị bắt, thư không thể gửi đến đích, hay được gửi đến đích nhưng nội dung bị sửa đổi
Hai vị tướng A1 và A2 cần thống nhất với nhau về việc tấn công thành phố B, và thời gian cả 2 cùng xuất quân. Bởi cả 2 chỉ có thể chiến thắng khi và chỉ khi họ tấn công vào cùng một thời điểm. Hay nói cách khác, họ cần đạt được sự đồng thuận với nhau về thời gian tấn công

Tưởng chừng như bài toán có thể giải quyết một cách đơn giản là trong 2 người bầu ra một chỉ huy, và đó là người đưa ra mốc thời gian tấn công gửi cho người kia thế là xong. Nhưng vấn đề nằm ở chỗ làm thế nào (chỉ bằng cách gửi message và xử lý message nhận được) để cả 2 có thể biết một cách chắc chắn rằng: "Cả 2 chúng ta đã đồng thuận và sẽ cùng tấn công vào thời điểm XX:YY ngày ZZ"

Chúng ta hãy dành chút thời gian để nói rõ về vấn đề ở đây nhé

Vị tướng quân A1 có thể sẽ bắt đầu bằng cách gửi một message đến vị tướng A2, với nội dung "Hãy cùng tấn công vào 12:00 ngày 19/8". Tuy nhiên, sau khi gửi thư, vị tướng A1 hoàn toàn không thể biết được liệu rằng người đưa thư có thể chuyển message an toàn đến cho vị tướng A2 hay không.
Để chắc chắn, vị tướng A2 sẽ cần gửi một lời xác nhận đến cho vị tướng A1 với nội dung: "Tôi đã nhận được tin nhắn của anh, và sẽ cùng tấn công vào 12:00 ngày 19/8". Tuy nhiên, một lần nữa, người đưa thư hoàn toàn có thể bị bắt, và vị tướng A2 sẽ lại rơi vào tình trạng lo lắng xem rằng không biết ông A1 có nhận được lời confirm của mình hay không
Để chắc chắn hơn, vị tướng A1 có thể sẽ tiếp tục gửi một message với nội dung "Tôi đã nhận được lời xác nhận của anh về kế hoạch tấn công vào 12:00 ngày 19/8 rồi". Tuy nhiên, người đưa thư này lại có thể bị bắt :v

Cứ như vậy, ta sẽ thấy một cách rõ ràng rằng, dù có trải qua bao nhiêu vòng xác nhận đi chăng nữa, cũng sẽ không có cách nào để cho từng vị tướng chắc chắn rằng người kia đã đồng ý với kế hoạch tấn công của mình. Cả hai đều luôn bị đặt trong trạng thái băn khoăn, nghi ngờ xem không biết cái tin nhắn cuối cùng mình gửi có đến được đích hay không.

Bài toán 2 vị tướng quân là bài toán về vấn đề truyền thông máy tính (computer communication) đầu tiên được chứng mình là không có lời giải

Bài toán các vị tướng Byzantine

Bài toán các vị tướng Byzantine được đưa ra bởi 3 nhà khoa học máy tính Leslie Lamport, Robert Shostak và Marshall Pease trong một báo cáo khoa học mang tên "The Byzantine Generals Problem" vào năm 1982. Đây là bài toán tổng quát hoá của bài toán 2 vị tướng quân.

Bài toán các vị tướng Byzantine miêu tả về một nhóm các vị tướng trong đội quân Byzantine (quân đội đế quốc Đông La Mã), tiến hành vây hãm 1 thành phố. Các vị tướng cần trao đổi để đạt được đến 1 thoả thuận về kế hoạch tấn công thành phố đó. Trong trường hợp đơn giản nhất, họ thoả thuận về việc nên tấn công hay rút lui. Một số có thể muốn tấn công, nhưng một số thì lại muốn rút lui, và vấn đề là nếu chỉ có một bộ phận tấn công riêng lẻ, thì họ sẽ gặp thất bại, và đó là kế hoạch tồi tệ hơn việc cùng tấn công hoặc cùng rút lui.

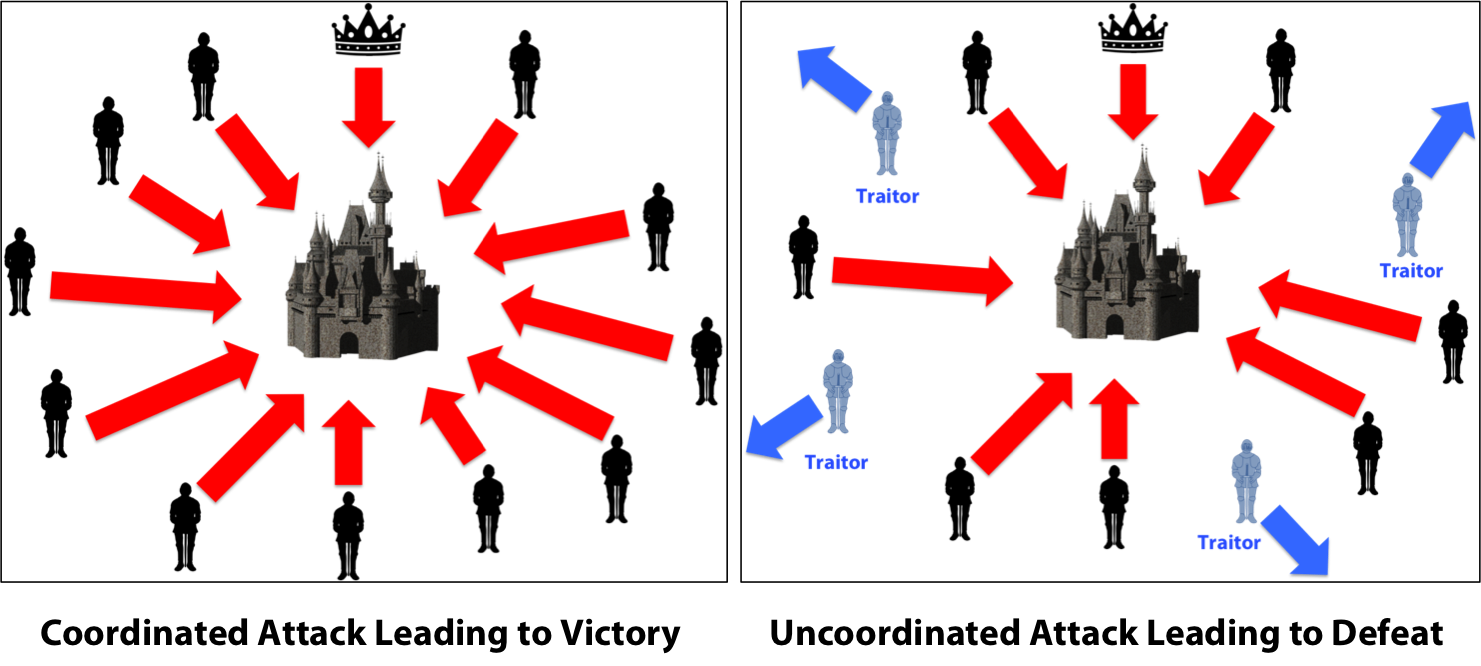
byzantine

Mọi thứ sẽ trở nên phức tạp khi mà một vị tướng sẽ có thể gửi tin nhắn đi cho các vị tướng khác. Chẳng hạn như trong trường hợp có 5 vị tướng, 2 ông đã phát tín hiệu muốn tấn công, 2 ông đã phát tín hiệu muốn rút lui, còn ông thứ 5 lại chơi trò 2 mang, nhắn với 2 ông muốn tấn công rằng mình muốn tấn công, còn nhắn với 2 ông muốn rút lui rằng mình sẽ rút lui. Khi đó phe tấn công nghĩ rằng tấn công là lựa chọn đa số và họ tấn công (và sẽ thất bại), phe rút lui thì nghĩ rằng rút lui là lựa chọn đa số và họ rút lui. Họ đã không đạt được sự đồng thuận (về việc có cùng ý kiến).

Mọi thứ sẽ còn phức tạp hơn nữa khi ta đặt trong trường hợp họ còn phải gửi tin nhắn thông qua một người đưa thư, nên hoàn toàn có khả năng xảy ra tình trạng người đưa thư ... bị bắt, thư không gửi được đến nơi, hay nội dung message bị sửa đổi.

Có khá nhiều giải pháp đã được đề cập trong báo cáo khoa học của Lamport, Shostak và Pease. Họ bắt đầu bằng một chú ý rằng, bài toán các vị tướng Byzantine, có thể giải quyết bằng cách quy về bài toán "Commander and Lieutenants" (chỉ huy & trung uý).

Bài toán như sau:

Người chỉ huy sẽ gửi lệnh cho các trung uý còn lại
Những vị trung uý có thể gửi các message cho nhau
Làm thế nào để những người trung thành có thể đạt được sự đồng thuận về một quyết định nào đấy (đơn giản như là tấn công hay rút lui)

Chú ý là kể cả trong trường hợp người chỉ huy là kẻ phản bội, thì tất cả (những vị tướng trung thành) vẫn vẫn cần đạt đến 1 sự đồng thuận.

3 nhà khoa học máy tính Lamport, Shostak và Pease có đưa ra thuật toán Oral Messages (OM) để giải quyết vấn đề này. Để cho tất cả đạt được 1 sự đồng thuận, ta cần dựa vào sự lựa chọn của số đông.

Tuy nhiên, trước hết cần giả định rằng:

Mọi message khi được gửi, đều sẽ được gửi đến đích một cách chính xác
Người nhận message sẽ biết được chính xác họ nhận từ ai
Có thể phát hiện ra sự vắng mặt của một message (chẳng hạn như ai đó không gửi)

Định lý: Với mỗi giá trị m là số lượng kẻ phản bội, thuật toán OM(m) có thể đạt được sự đồng thuận nếu có tổng cộng là hơn 3m số lượng các vị tướng quân.

Hay nói cách khác, nếu có tất cả là n vị chỉ huy, thì thuật toán OM sẽ đạt được sự đồng thuận khi có 2/3 là trung thành (hay không quá 1/3 là phản bội). Các bạn có thể xem thêm chi tiết về thuật toán OM tại đây hoặc đây

Để dễ tưởng tượng, chúng ta hãy cùng xem qua trường hợp đơn giản, với 4 vị tướng (gồm C, L1, L2, L3), và 1 kẻ phản bội, như sau:

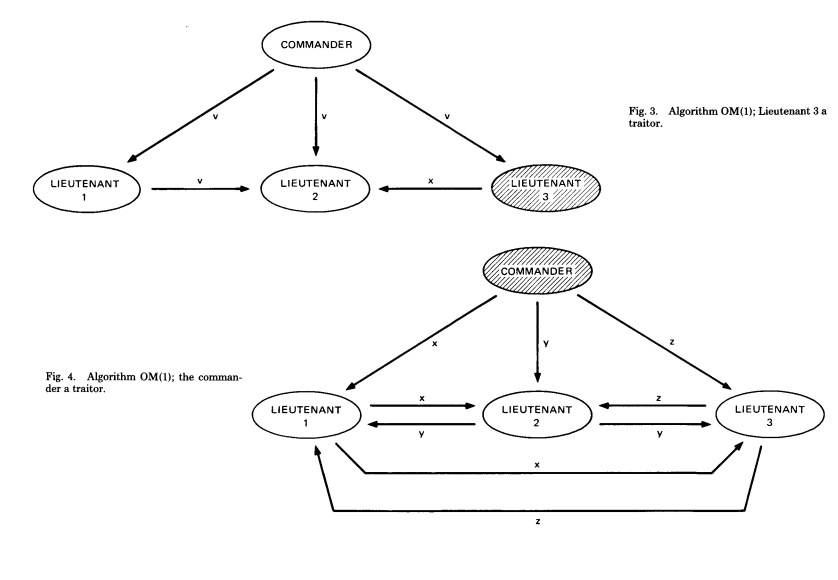
Byzantine Generals problem

Trường hợp 1, kẻ phản bội là L3. C sẽ broadcast message với nội dung v cho L1, L2, L3. L3 phản bội nên sẽ sửa đổi nội dung, và gửi x cho L2. Tuy nhiên, L2 sẽ nhận được v từ L1 và C và sẽ thấy là phần đông đã lựa chọn v. Từ đó những vị tướng trung thành, gồm C, L1 và L2 sẽ đạt được sự đồng thuận là phương án v, mặc cho L3 có broadcast message x
Trường hợp 2, kẻ phản bội là C. C có thể gửi x cho L1, gửi y cho L2 và gửi z cho L3. L1, L2, L3 đều trung thành, nên sẽ broadcast message mà họ nhận được cho những người khác. Như vậy L1 sẽ nhận được đủ cả 3 lệnh là x (từ C), y (từ L2) và z (từ L3). Trông có vẻ như không thể quyết định được đấy, nhưng thực chất, quyết định của cả 3 người sẽ là giống nhau, vì cùng là majority(x,y,z). Nếu x, y, z mang những nội dung hoàn toàn khác nhau, và không thể tính trọng số, tất cả sẽ theo lựa chọn default, ở đây có thể là rút quân chẳng hạn.

Hệ thống chịu lỗi Byzantine

Hệ thống chịu lỗi Byzantine, hay Byzantine Fault Tolerance (BFT), là hệ thống có thể giải quyết được vấn đề của bài toán các vị tướng quân Byzantine.

Việc xây dựng một hệ thống chịu lỗi Byzantine là một điều cần thiết, nhưng cũng cực kỳ khó khăn trong một hệ thống phân tán.

Năm 1999, 2 nhà khoa học máy tính Miguel Castro và Barbara Liskov giới thiệu thuậnt toán "Practical Byzantine Fault Tolerance" (PBFT) có thể quản lý các trạng thái Byzantine với một hiệu suất cao, có thể xử lý hàng nghìn requests một giây với độ trễ cực thấp.

Sau sự ra đời của PBFT, hàng loại các BFT protocols khác cũng được giới thiệu với nhiều sự cải tiến về mặt hiệu năng, và được ứng dụng rộng rãi hơn.

Byzantine Fault Tolerance hiện hữu trong những hệ thống engine của máy bay, tên lửa, nhà máy hạt nhân ... những thứ cần phải đưa ra quyết định dựa vào thông tin nhận được từ rất nhiều các cảm biến khác nhau.

Byzantine Generals Problem & Blockchain & Consensus

Giải thích một hồi về 2 generals problem, về Byzantine Generals Problem rồi Byzantine Fault Tolerance, chắc cũng có nhiều bạn đang thắc mắc rằng liệu nó có liên quan gì đến Blockchain nhỉ

Blockchain là một cuốn sổ cái được chia sẻ cho mọi thành viên trong một mạng lưới phi tập trung (decentralized). Ở đó, không hề có một bên thứ 3 được tin tưởng để quản lý sự vận hành của nó, mà tự các thành viên của hệ thống phải tương tác với nhau để đi đến một sự đồng thuận (consensus). Hay nói cách khác, một hệ thống Blockchain cần có cách để chịu lỗi Byzantine.

Khi Bitcoin, blockchain đầu tiên ra đời, cha đẻ của nó, Nakamoto Satoshi cũng đã giới thiệu một một phương pháp để giải quyết bài toán các vị tướng quân, được gọi dưới cái tên Proof-of-Work (PoW), hay "bằng chứng công việc". Các bạn có thể tìm hiểu thêm về Proof of Work cũng như cách thức hoạt động của mạng lưới Bitcoin thông qua 2 video trên Viblo tại đây và đây

Nakamoto Satoshi cũng từng trực tiếp giải thích về cách Bitcoin dùng PoW để giải quyết bài toán các vị tướng Byzantine trong một email gửi đi ngày 14/11/2008, các bạn có thể xem qua tại đây

Đoạn trao đổi của Nakamoto Satoshi về Byzantine Generals Problem, các bạn có thể xem qua (lười dịch quá )

Cũng cần phải nhắc đến rằng, bài toán Byzantine trên mạng lưới Blockchain đã được đơn giản hơn, nhờ vào việc sử dụng chữ ký điện tử (Digital Signature). Với những đặc tính mà nó mang lại như:

Authentication (tính xác thực): chữ ký điện tử có thể dùng để xác thực xem ai là người đã gửi message. Chỉ có người quyền sở hữu với private key mới có thể tạo ra chữ ký điện tử cho một message.
Integrity (tính toàn vẹn): message không thể bị sửa đổi trong quá trình truyền đi. Nếu điều đó xảy ra, chữ ký điện tử sẽ trở nên không hợp lệ nữa.
Non-repudiation (không thể chối cãi): một message cùng chữ ký điện tử đã được gửi đi, thì người đã ký nó không thể phủ nhận việc mình đã tạo và ký message

Như các bạn thấy, chữ ký điện tử đã giúp tạo ra một môi trường có những điều kiện như đã được đề cập ở phần "Bài toán các vị tướng Byzantine" phía trên đấy

Bên cạnh PoW, ngày nay các blockchain còn có sử dụng nhiều Consensus Protocol khác. Ví dụ như Neo dùng Delegated Byzantine Fault Tolerance, hay nền tảng Hyperledge Fabric của Linux Foundation dùng Practical Byzantine Fault Tolerance (PBFT), gần giống với giải pháp consensus mà Tendermint cung cấp.

Đặc biệt, nền tảng Blockchain lớn bậc nhất thế giới hiện nay, Ethereum cũng đã công bố kế hoạch chuyển từ Proof of Work sang Proof of Stake (PoS - Bằng chứng cổ phần) trong thời gian tới. PoS trên nền tảng Ethereum, với tên mã là Casper sẽ xuất hiện với phiên bản đầu tiên là Casper: Friendly Finality Gadget (Casper FFG), hay Vitalik Casper (do đây là phiên bản được thực hiện bởi nhóm nghiên cứu do Vitalik Buterin dẫn đầu). Đây sẽ là phiên bản Byzantine Fault Tolerance-style proof of stake, tức sẽ có những điểm giống với các thuật toán BFT truyền thống.

Trong các bài viết sau, mình sẽ nói rõ hơn về PoS, cũng như Ethereum Casper FFG, các bạn chú ý theo dõi nhé

References

Computer Science Blockchain Byzantine Generals Problems Byzantine Fault Tolerance Consensus