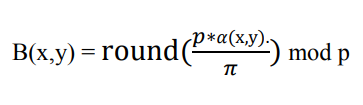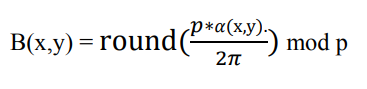Tìm hiểu về phương pháp mô tả đặc trưng HOG (Histogram of Oriented Gradients)

HOG là viết tắt của Histogram of Oriented Gradient - một loại “feature descriptor”. Mục đích của “feature descriptor” là trừu tượng hóa đối tượng bằng cách trích xuất ra những đặc trưng của đối tượng đó và bỏ đi những thông tin không hữu ích. Vì vậy, HOG được sử dụng chủ yếu để mô tả hình dạng và sự xuất hiện của một đối tượng trong ảnh.

Bản chất của phương pháp HOG là sử dụng thông tin về sự phân bố của các cường độ gradient (intensity gradient) hoặc của hướng biên (edge directins) để mô tả các đối tượng cục bộ trong ảnh. Các toán tử HOG được cài đặt bằng cách chia nhỏ một bức ảnh thành các vùng con, được gọi là “tế bào” (cells) và với mỗi cell, ta sẽ tính toán một histogram về các hướng của gradients cho các điểm nằm trong cell. Ghép các histogram lại với nhau ta sẽ có một biểu diễn cho bức ảnh ban đầu. Để tăng cường hiệu năng nhận dạng, các histogram cục bộ có thể được chuẩn hóa về độ tương phản bằng cách tính một ngưỡng cường độ trong một vùng lớn hơn cell, gọi là các khối (blocks) và sử dụng giá trị ngưỡng đó để chuẩn hóa tất cả các cell trong khối. Kết quả sau bước chuẩn hóa sẽ là một vector đặc trưng có tính bất biến cao hơn đối với các thay đổi về điều kiện ánh sáng.

Có 5 bước cơ bản để xây dựng một vector HOG cho hình ảnh, bao gồm:

1. Tiền xử lý
2. Tính gradient
3. Tính vector đặc trưng cho từng ô (cells)
4. Chuẩn hóa khối (blocks)
5. Tính toán vector HOG

1. Tiền xử lý

Trong bài toán này, để thuận tiện cho việc chia đều hình ảnh thành các khối, ô và tính toán đặc trưng ở các bước tiếp theo, chúng ta cần resize kích thước tất cả các hình ảnh trong tập dữ liệu về một kích thước chung.

Trong các ví dụ được trình bày trong bài viết này, kích thước chung cho 1 hình ảnh sẽ mặc định là 64x128

2. Tính Gradient

Đây là bước đầu tiên, được thực hiện bằng hai phép nhân chập ảnh gốc với 2 chiều, tương ứng với các toán tử lấy đạo hàm theo hai hướng Ox và Oy. Trong đó, 2 hướng tương ứng đó là:

T là phép toán chuyển vị ma trận.

Nghe có vẻ khó hiểu nhỉ, xem hình ảnh dưới đây để có cái nhìn trực quan hơn nhé.

Và nếu bạn có một ảnh input là I, ta sẽ có 2 ảnh đạo hàm riêng theo 2 hướng đó, theo công thức:

Khi đó, bạn có thể tính được Gradient bao gồm hai thành phần cường độ(Gradient Magnitude) và hướng(Gradient Derection) theo công thức (*):

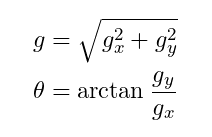
Ví dụ: Giả sử ta có một điểm ảnh như sau

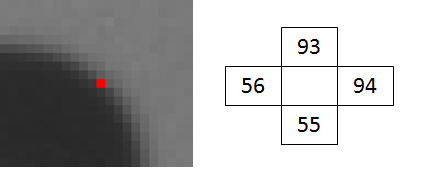
Chúng ta sẽ áp dụng các công thức trên để tính được gradient của điểm ảnh này:

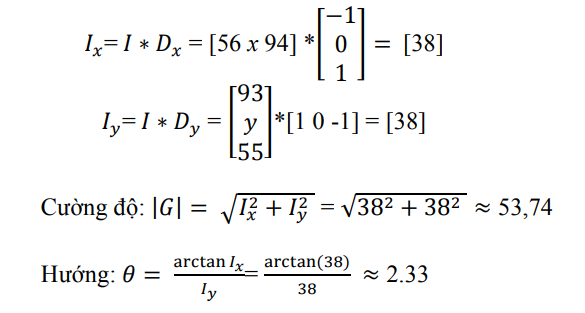
Đối với hình ảnh màu, gradient của ba kênh(red, green và blue) được đánh giá. Độ lớn của gradient tại một điểm ảnh là giá trị lớn nhất của cường độ gradient của ba kênh, và góc là góc tương ứng với gradient tối đa.

Sau bước này, kết quả thu được sẽ là:

3. Tính vector đặc trưng cho từng ô (cells)

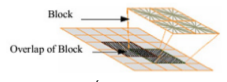
Để tính toán vector đặc trưng cho từng ô (cell), chúng ta cần chia hình ảnh thành các block, mỗi block lại chia đều thành các cell. Để xác định được số block, chúng ta sẽ sử dụng công thức sau:

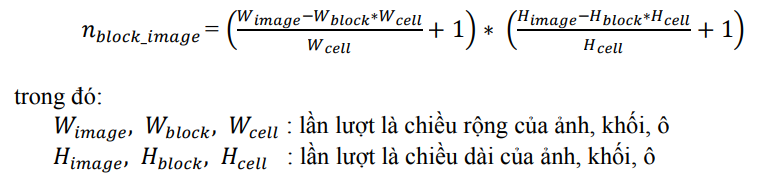
Các block có thể xếp chồng lên nhau như hình:

Sau khi xác định số block và kích thước mỗi block, cell, để tính toán vector đặc trưng cho từng cell, chúng ta cần:

1. Chia không gian hướng thành p bin(số chiều vector đặc trưng của ô).
2. Rời rạc hóa góc hướng nghiêng tại mỗi điểm ảnh vào trong các bin.

Giả sử góc hướng nghiêng tại pixel ở vị trí (x,y) có độ lớn là alpha(x,y)

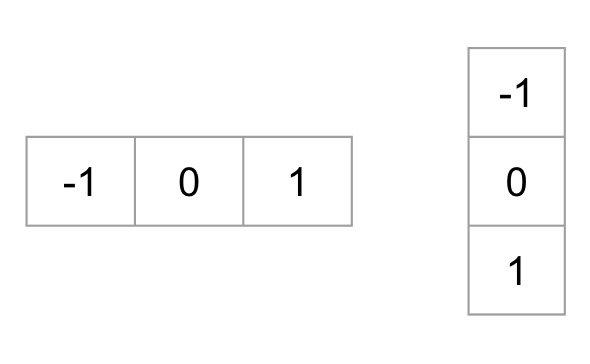
• Trường hợp rời rạc hóa unsigned-HOG với p=9:

• Trường hợp rời rạc hóa signed-HOG với p=18:

Giá trị bin được định lượng bởi tổng cường độ biến thiên của các pixels thuộc về bin đó. Sau khi tính toán đặc trưng ô, ta sẽ nối các vector đặc trưng ô để thu được vector đặc trưng khối. Số chiều vector đặc trưng khối tính theo công thức :

Ví dụ: Trong trường hợp này, hình ảnh của chúng ta có kích thước là 64x128, ta sẽ chia mỗi hình ảnh thành các block có kích thước 16x16. Mỗi block sẽ bao gồm 4 cell, mỗi cell có kích thước là 8x8.

Tiếp theo, tiến hành tính toán đặc trưng HOG tại mỗi cell sử dụng không gian hướng 9 bin, trường hợp “unsigned-HOG”. Hướng gradient sẽ chạy trong khoảng 0 độ đến 180 độ, trung bình 20 độ mỗi bin.

Tại mỗi cell, xây dựng một biểu đồ cường độ gradient bằng cách vote các pixel vào biểu đồ. Trọng số vote của mỗi pixel phụ thuộc hướng và cường độ gradient (được tính toán từ bước 2) của pixel đó. Ví dụ:

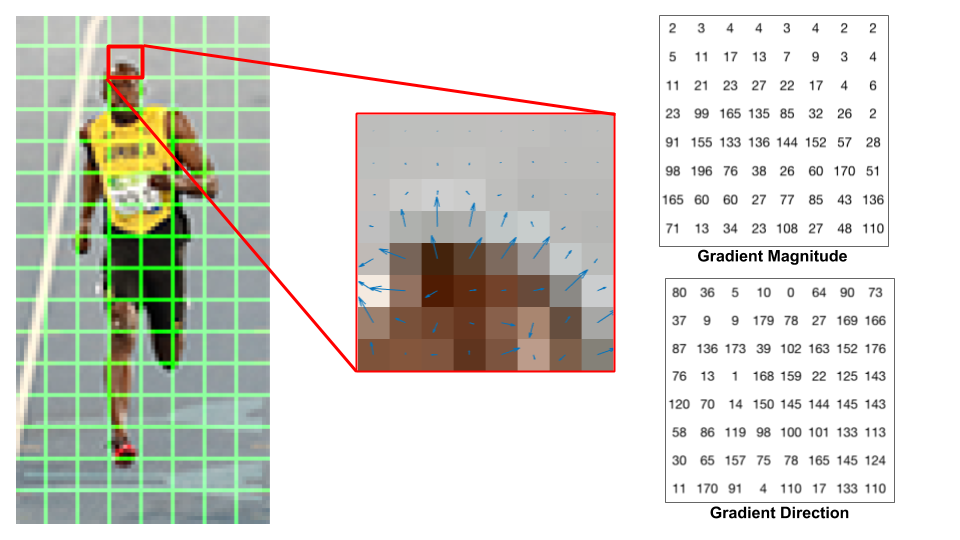
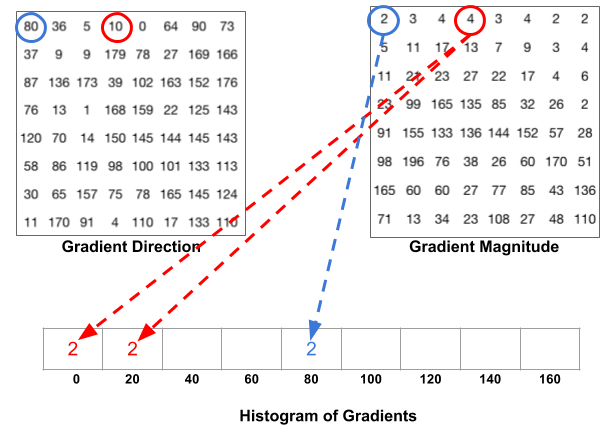
Như trong hình ảnh trên, đầu tiên là pixel có bao quanh màu xanh lam. Nó có hướng 80 độ và cường độ là 2, vì vậy ta thêm 2 vào bin thứ 5 (hướng 80 độ). Tiếp theo là pixel có bao quanh màu đỏ. Nó có hướng 10 độ và cường độ 4. Vì không có bin 10 độ, nên ta vote cho bin 0 độ và 20 độ, mỗi bin thêm 2 đơn vị. Sau khi vote hết các pixel trong một cell kích thước 8x8 vào 9 bin, ta có thể thu được kết quả như sau:

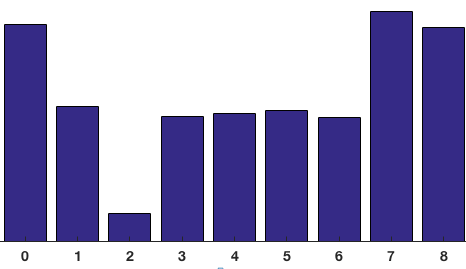
4. Chuẩn hóa khối (blocks)

Để tăng cường hiệu năng nhận dạng, các histogram cục bộ sẽ được chuẩn hóa về độ tương phản bằng cách tính một ngưỡng cường độ trong một khối và sử dụng giá trị đó để chuẩn hóa tất cả các ô trong khối. Kết quả sau bước chuẩn hóa sẽ là một vector đặc trưng có tính bất biến cao hơn đối với các thay đổi về điều kiện ánh sáng.

Đầu tiên, hãy xem xét ảnh hưởng của việc chuẩn hóa tới các vector gradient trong ví dụ sau:

Trong hình ảnh trên, trường hợp đầu tiên là một ô của hình ảnh ban đầu. Trường hợp thứ hai, tất cả các giá trị pixel đã được tăng lên 50. Trong trường hợp thứ ba, tất cả các giá trị pixel được nhân với 1.5. Dễ dàng thấy được, trường hợp thứ ba hiển thị độ tương phản gia tăng. Ảnh hưởng của phép nhân là làm các điểm ảnh sáng trở nên sáng hơn nhiều, trong khi các điểm ảnh tối chỉ sáng hơn một chút, do đó làm tăng độ tương phản giữa các phần sáng và tối của hình ảnh.

Hãy nhìn vào các giá trị pixel thực tế và sự thay đổi của vector gradient của ba trường hợp trên trong hình ảnh sau:

• Các con số trong các ô là giá trị pixel của các điểm ảnh lân cận điểm ảnh được đánh dấu màu đỏ.
• Delta F là đạo hàm theo riêng hai hướng của điểm ảnh ([Ix, Iy])
• | Delta F| là giá trị cường độ điểm ảnh (Gradient Magnitude), tính theo công thức (*)

Trong trường hợp một và hai, giá trị cường độ vector gradient của chúng tương đương nhau, nhưng trong trường hợp thứ ba, cường độ vector gradient đã tăng lên 1.5 lần. Nếu chia ba vector bằng độ lớn tương ứng, ta sẽ nhận được các kết quả tương đương cho cả ba trưởng hợp. Vì vậy, trong ví dụ trên, chúng ta thấy rằng bằng cách chia các vector gradient theo độ lớn của chúng, chúng ta có thể biến chúng thành bất biến để thay đổi độ trương phản.

Có nhiều phương pháp có thể được dùng để chuẩn hóa khối. Gọi v là vector cần chuẩn hóa chứa tất cả các histogram của mội khối. ‖v(k)‖ là giá trị chuẩn hóa của v theo các chuẩn k=1, 3 và e là một hằng số nhỏ. Khi đó, các giá trị chuẩn hóa có thể tính bằng một trong những công thức sau:

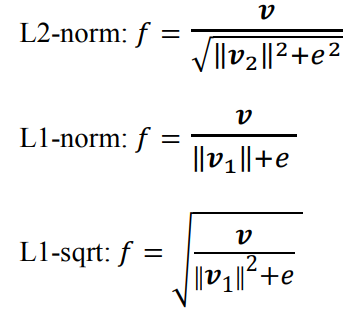
Ghép các vector đặc trưng khối sẽ thu được vector đặc trưng R-HOG cho ảnh. Số chiều vector đặc trưng ảnh tính theo công thức :

5. Tính toán vector đặc trưng HOG

• Với mỗi hình ảnh kích thước 64x128, chia thành các block 16x16 chồng nhau, sẽ có 7 block ngang và 15 block dọc, nên sẽ có 7x15 = 105 blocks.
• Mỗi block gồm 4 cell. Khi áp dụng biểu đồ 9-bin cho mỗi cell, mỗi block sẽ được đại diện bởi một vector có kích thước 36x1.

• Vì vậy, khi nối tất cả các vector trong một block lại với nhau, ta sẽ thu được vector đặc trưng HOG của ảnh có kích thước 105x36x1 = 3780x1.

Link tài liệu tham khảo:

Histogram of Oriented Gradients

HOG Person Detector Tutorial