Phổ Fourier (Fourier Spectrum) của một tín hiệu cho thấy nội dung tín hiệu đó trong miền tần số. Điều này làm cho phổ (Spectrum) trở thành một miền dễ chịu để làm việc bởi vì ta có thể kiểm tra các tín hiệu một cách trực quan. Trong thực tế, ta làm việc với các tín hiệu thời gian rời rạc, sao cho biến đổi miền thời gian-tần số tương ứng là biến đổi Fourier rời rạc. Phép biến đổi này ánh xạ tín hiệu $x_n$ độ dài $N$ thành một biểu diễn miền tần số số phức $X_k$ của $N$ hệ số như sau:

$$X_{k}=\sum_{n=0}^{N-1} x_{n} e^{-i 2 \pi \frac{k n}{N}}$$

Đối với các đầu vào có giá trị thực, các thành phần tần số dương và âm là các liên hợp phức (complex conjugates) của nhau, sao cho chúng giữ lại N đơn vị thông tin duy nhất. Vì spectrum là các vectơ là số phức, ta sẽ visualize magnitude $|X_k|$ hoặc power $|X_k|^2$ của nó. Với tín hiệu đầu vào như bên dưới:

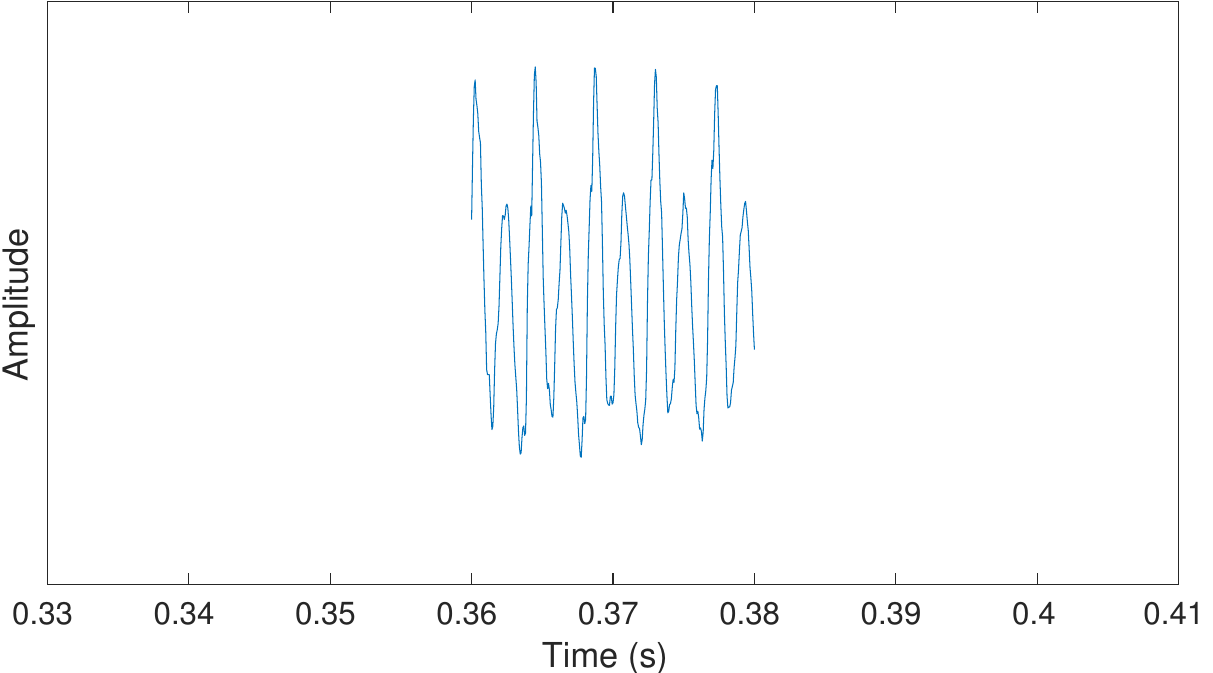
Ta sẽ có được magnitude spectrum: Và power spectrum:

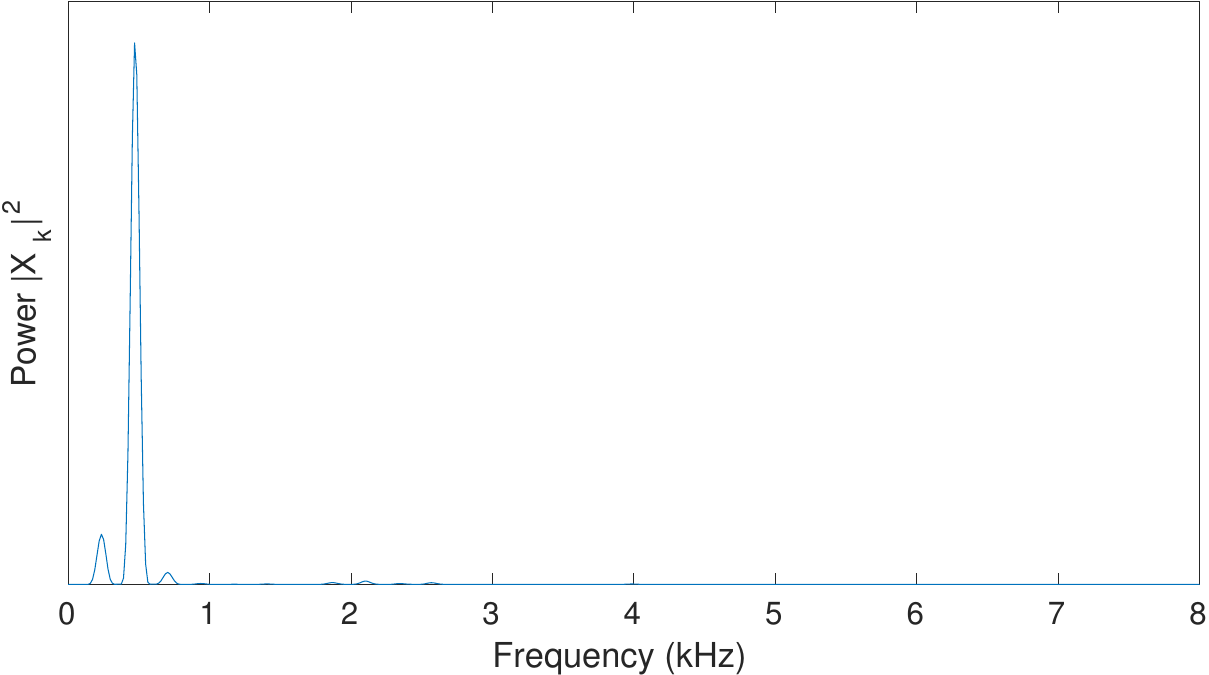
Từ phổ biên độ (magnitude spectrum) ta sẽ trích xuất được rất nhiều đặc trưng của tín hiệu đầu vào.

Spectral Centroid và Spectral Spread

Spectral centroid và spectral spread là hai phương pháp đơn giản để trích xuất thông tin về vị trí và hình dạng phổ. Spectral centroid là trung tâm của ‘trọng lực’ của phổ. Giá trị của trung tâm phổ $C_i$ của frame âm thanh thứ $i$ được xác định là:

$$C_{i}=\frac{\sum_{k=1}^{N} k X_{i}(k)}{\sum_{k=1}^{N} X_{i}(k)}$$

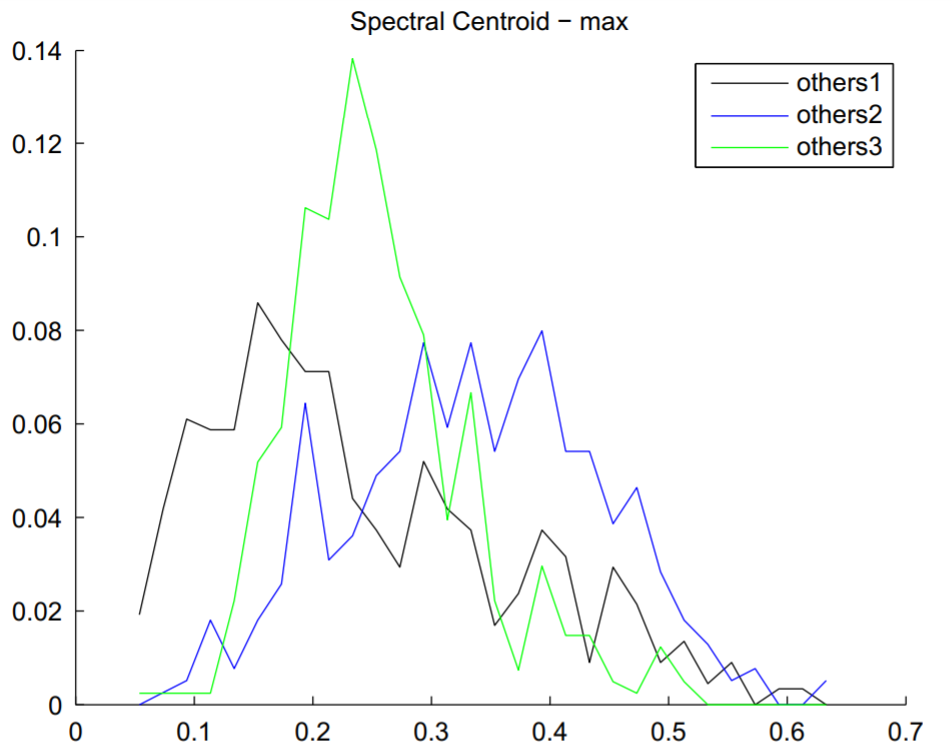
Với spectral centroid, ta có thể thấy rằng các giá trị cao tương ứng với âm thanh sáng hơn. Hình bên dưới là biểu đồ giá trị tối đa của tâm phổ cho các frame âm thanh từ ba loại âm thanh môi trường. Có thể thấy rằng class ‘other1’ - chủ yếu bao gồm tiếng ồn nền và khoảng lặng…, thể hiện các giá trị thấp hơn ở vùng giá trị thấp, trong khi các giá trị cao ở các class 'other3' thể hiện âm thanh biến đổi đột ngột.

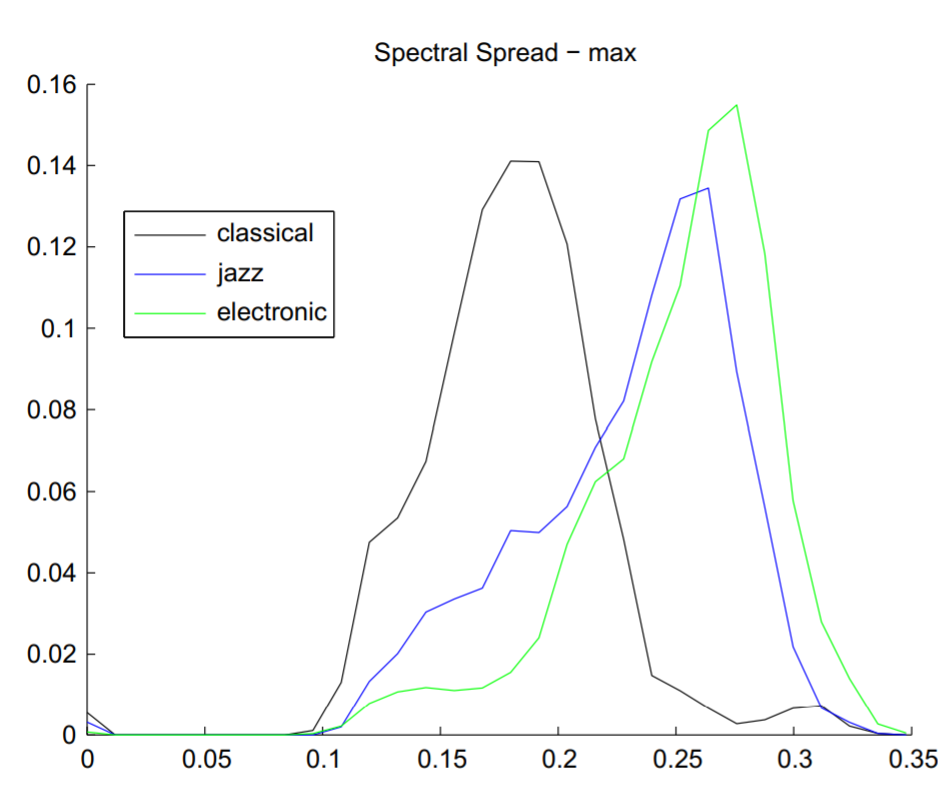
Spectral spread đo sự phân bố của phổ xung quanh tâm của nó:

$$S_{i}=\sqrt{\frac{\sum_{k=1}^{N}\left(k-C_{i}\right)^{2} X_{i}(k)}{\sum_{k=1}^{N} X_{i}(k)}}$$

Như vậy, các giá trị thấp của Spectral spread tương ứng với các tín hiệu có phổ tập trung dày đặc quanh tâm quang phổ. Hình bên dưới thể hiện biểu đồ giá trị tối đa của chuỗi Spectral spread cho các frame âm thanh xuất phát từ ba class âm nhạc (classical, jazz và electronic). Trong ví dụ cụ thể này, kết quả cho thấy phổ của các trích đoạn của nhạc điện tử (thường) được lan truyền rộng rãi hơn ra quanh tâm của nó so với nhạc cổ điển và nhạc jazz. Tuy nhiên kết quả này có thể sẽ không giống nhau cho mọi bản nhạc trong các thể loại.

Spectral flux

Spectral flux đo sự thay đổi phổ giữa frame liên tiếp và được tính là chênh lệch bình phương giữa độ lớn chuẩn hóa của phổ của hai cửa sổ ngắn hạn liên tiếp:

$$F l_{(i, i-1)}=\sum_{k=1}^{W f_{L}}\left(E N_{i}(k)-E N_{i-1}(k)\right)^{2}$$

Trong đó:

$$E N_{i}(k)=\frac{X_{i}(k)}{\sum_{l=1}^{N} X_{i}(l)}$$

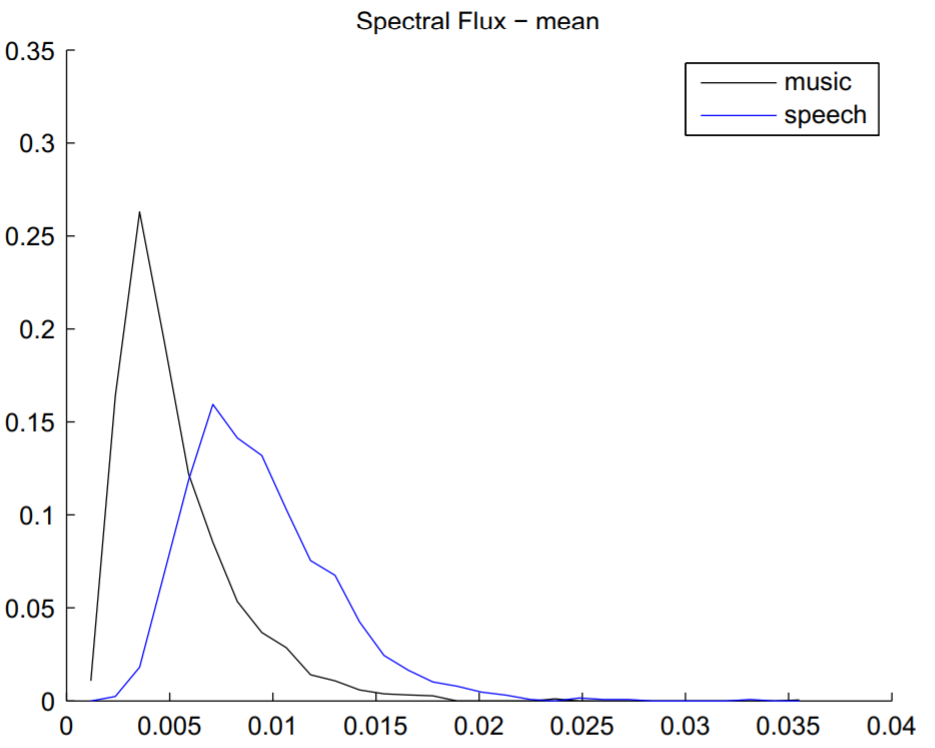
là hệ số DFT đã chuẩn hóa thứ $k$ của frame thứ $i$. Hình dưới trình bày biểu đồ giá trị trung bình của chuỗi spectral flux của các frame từ hai class: music và speech. Có thể thấy rằng các giá trị của spectral flux của speech cao hơn so với music. Điều này là do sự thay đổi phổ cục bộ xảy ra thường xuyên hơn trong các tín hiệu lời nói do sự thay đổi nhanh chóng giữa các âm vị.

Spectral rolloff

Đặc trưng này được định nghĩa là tần số mà dưới mức đó một phần trăm nhất định (thường là khoảng 90%) phân bố cường độ của phổ được tập trung. Do đó, nếu hệ số DFT thứ $m$ tương ứng với spectral rolloff của frame thứ $i$, thì nó thỏa mãn phương trình sau:

$$\sum_{k=1}^{m} X_{i}(k)=C \sum_{k=1}^{N} X_{i}(k)$$

Trong đó C là tỷ lệ phần trăm được thông qua (tham số người dùng quyết định). Tần số spectral rolloff thường được chuẩn hóa bằng cách chia nó với $N$, do đó, nó nhận các giá trị trong khoảng từ 0 đến 1. Loại chuẩn hóa này ngụ ý rằng giá trị 1 tương ứng với tần số tối đa của tín hiệu, tức là một nửa tần số lấy mẫu.

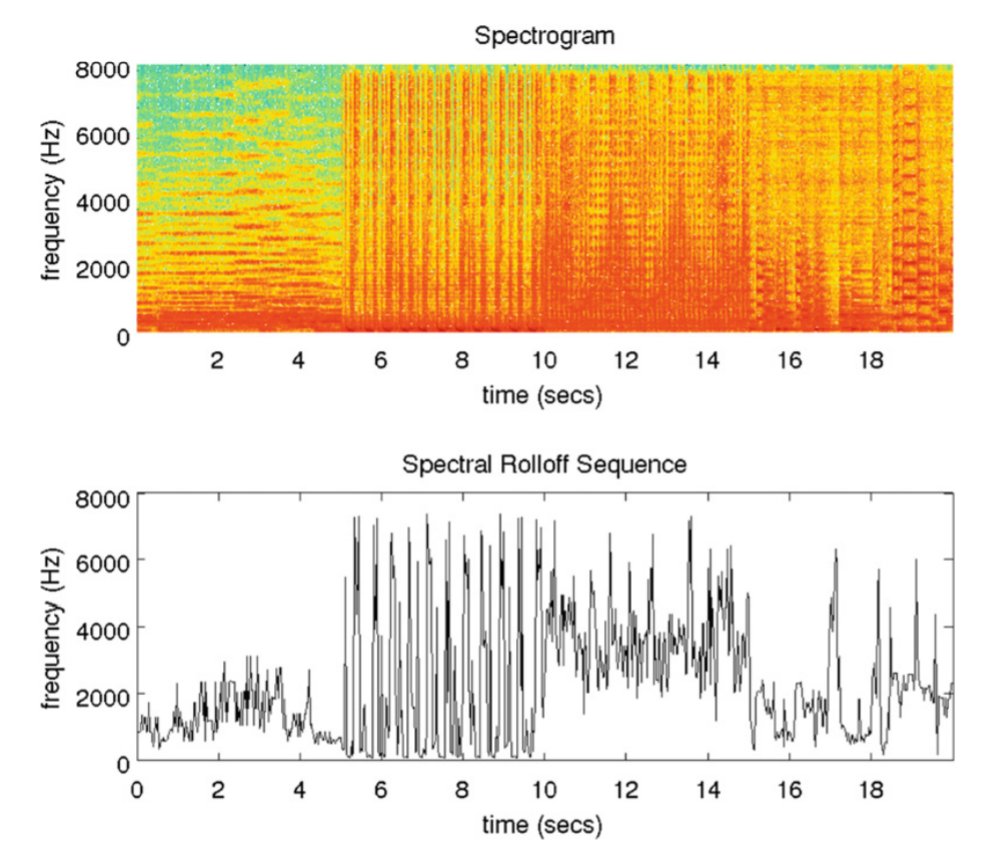
Spectral rolloff cũng có thể được coi là một mô tả hình dạng phổ của tín hiệu âm thanh và có thể được sử dụng để phân biệt giữa âm thanh tiếng nói và âm thanh không phải tiếng nói. Nó cũng có thể được sử dụng để phân biệt giữa các loại nhạc khác nhau. Hình dưới trình bày một ví dụ về spectral rolloff. Hình này được trích xuất từ một bản nhạc tổng hợp (dài 20 giây) bao gồm bốn đoạn trích nhạc khác nhau (mỗi đoạn 5 giây). Phần đầu tiên của bản nhạc tổng hợp bắt nguồn từ âm nhạc cổ điển, phần thứ hai và thứ ba bắt nguồn từ hai bản nhạc điện tử khác nhau, trong khi phần cuối cùng đến từ một bản nhạc jazz. Có thể dễ dàng quan sát thấy rằng các bản nhạc điện tử tương ứng với các giá trị cao hơn của chuỗi spectral rolloff. Ngoài ra, sự biến đổi cũng rõ ràng hơn đối với loại nhạc này. Đó là một điều dễ hiểu nếu chúng ta xem xét hình dạng của các phổ tương ứng: trong các phần cổ điển và jazz, phần lớn năng lượng quang phổ tập trung ở tần số thấp hơn và chỉ có thể nhìn thấy một số sóng điều hòa ở vùng tần số trung và cao hơn. Mặt khác, trong ví dụ này, âm nhạc điện tử mang lại phổ rộng hơn và do đó các giá trị spectral rolloff tương ứng cao hơn.

Kết luận

Trên đây là một vài đặc trưng về spectral của tín hiệu âm thanh. Ngoài ra vẫn còn rất nhiều đặc trưng khác cho ta khai thác như spectral skewness, spectral kurtosis,... Các đặc trưng này đều trích xuất dễ dàng và nhỏ gọn, phù hợp với nhiều bài toán khác nhau.