Những mô hình trợ thủ đắc lực trong các mô hình Deep learning [Phần 1]

Bài đăng này đã không được cập nhật trong 3 năm

I. Giới thiệu

Khi làm việc với các bài toán về computer vision, chúng ta đã quá quen với các mô hình như ResNet, InceptionNet, EfficientNet, .... Các mô hình này thường đóng vai trò như một bộ trích xuất đặc trưng từ đầu vào. Có thể ví von rằng, làm một bài toán computer vision như tham gia vào một cuộc đọ súng. Trong đó hàm loss chính là quân địch, diệt càng nhiều càng tốt. Quân ta bao gồm lực lượng chính thiện chiến như các mạng ResNet, EfficientNet, .... Để bổ sung hỗ trợ tốt nhất cho lực lượng chính ngoài ra trong Deep learning chúng ta còn có các mô hình đóng vai trò trợ thủ đắc lực kề vai sát cánh giúp lực lượng chính "tiêu diệt " hay tối ưu được nhiều "quân địch".

Và hôm nay mình xin giới thiệu cho các bạn một vài "trợ thủ" mà cá nhân mình rất hay dùng bên cạnh mô hình chính. Đó là Spatial Transformer Network (STN) và Squeeze-and-Excitation Network. Các mô hình này rất linh hoạt, nhẹ, mất ít chi phí tính toán, có thể tùy ý lắp ghép vào các mô hình chính trong khi có thể gia tăng đáng kể độ chính xác cho mô hình.

Trong bài đầu tiên này mình sẽ giới thiệu và phân tích về tay "trợ thủ" đầu tiên Squeeze and Excitation Networks. Mình cũng không biết dịch sang tiếng Việt thế nào nên mình xin phép các bạn tên mô hình sẽ để tạm thời là tiếng Anh nhé. Mình cùng đi phân tích xem có gì hay ho nào

II. Một chút về mạng tích chập

Ảnh minh họa

Các mô hình tích chập hay CNNs (Convolution neural networks) có trung tâm là các hàm tích chập giúp cho mô hình có thể trích xuất được những đặc trưng giàu thông tin bằng cách kết hợp thông tin không gian (H x W) và thông tin giữa các kênh bằng một tập hợp các kernel. Những đặc trưng được trích xuất này là những đặc trưng mà chúng ta kỳ vọng là tiêu biểu nhất cho bài toán tương ứng được thực hiện thông qua đó giúp cải thiện độ chính xác. Và đây cũng chính là nhiệm vụ chính của các mô hình CNN trong các bài toán về thị giác máy tính.

Có một số nghiên cứu đã chỉ ra rằng có thể gia tăng sức mạnh biểu diễn của các mô hình CNN bằng cách tích hợp một cơ chế có thể học ví dụ như thêm các shallow network vào trong mô hình để có thể học được mối tương quan về mặt không gian giữa các đặc trưng. Khái niệm không gian ở đây chúng ta có thể hiểu là không gian hai chiều cao và rộng (height và width). Một trong những mô hình tiêu biểu đã sử dụng phương pháp đó có thể kể đến là mô hình Inception Net.

Tuy nhiên như đã nói bên trên các hàm tích chập trích xuất thông tin dựa trên kết hợp cả thông tin không gian (HxW) và thông tin giữa các kênh. Do đó một ý tưởng đã nảy ra "Chúng ta tăng cường thông tin theo không gian rồi. Tại sao chúng ta lại không tăng cường thông tin giữa chính các kênh ? ". Và đó là lý do mà mô hình Squeeze and Excitation sinh ra.

III. Mô hình Squeeze and Excitation (SE)

SE là một mạng khá đơn giản chỉ gồm vài lớp nhằm tăng cường thông tin giữa các kênh qua đó tăng chất lượng biểu diễn của mô hình CNN. SE làm được điều đó bằng cách sử dụng toàn bộ thông tin sau đó nhấn mạnh có chọn lọc vào từng kênh có đặc trưng quan trọng và ít chú ý vào những kênh ít quan trọng hơn. Cá nhân mình thấy khái niệm này khá giống với ý tưởng Self attention rất được hay dùng trong các bài toán xử lý ngôn ngữ tự nhiên cũng dùng đầu vào là chính nó để chú ý những thông tin quan trọng của chính nó. Nếu các bạn tò mò muốn tìm hiểu rõ hơn về khái niệm Self attention thì các bạn có thể theo dõi bài viết Tản mạn về Self atteion của mình để tìm hiểu rõ hơn nhé.

1. Kiến trúc mạng

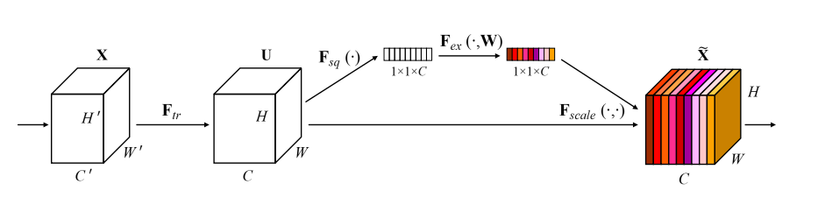
Squeeze and Excitation Block

Giải thích một số ký hiệu:

X: ảnh đầu vào có kích thước H' x W' x C'
$F_{tr}:$ tập hợp các phép biến đổi: một vài lớp convolution, hoặc 1 stage của VGG, 1 block trong ResNet, ....
U: feature map hay đặc trưng được trính xuất từ ảnh đầu vào bởi các phép biển đổi $F_{tr}$ . U có kích thước H x W x C

Nào chúng ta cùng miêu tả kĩ một chút về kiến trúc của khối SE này nhé

Bước 1:. Ảnh đầu vào X đi qua một tập hợp các phép biển đổi $F_{tr}$ trích xuất ra bản đồ đặc trưng (features map) U.

Bước 2:. Feature map U (H x W x C) được đi qua hàm squeeze sinh ra một ma trận miêu tả đặc trưng của từng kênh (1 x 1 x C) bằng cách tổng hợp features map U theo chiều H và W. Ví dụ hàm squeeze ở đây có thể là global average pooling.

Bước 3: Theo sau hàm squeeze là hàm excitation. Hàm excitation đóng vai trò là cơ chế miêu tả sự phụ thuộc giữa các kênh với nhau. Hàm lấy đầu vào là ma trận tổng hợp đặc trưng của từng kênh được tính toán từ bước 2 qua một vài lớp biến đổi như convolution, hàm activation, .... và cuối cùng qua hàm gate sản sinh ra trọng số chú ý cho từng kênh. Những trọng số này sau đó được nhân với feature map U để tính ra output của khối SE. Output lúc này của khối SE chỉ còn chứa những thông tin thực sự quan trọng cho bài toán. Hàm gate ở đây thường là hàm sigmoid.

Có câu hỏi đặt ra rằng tại sao ta lại dùng hàm sigmoid chứ không phải là hàm softmax mà chúng ta vẫn hay dùng trong mô đun attention ? Đây cũng là một điểm khác biệt của mô hình SE và Attention nói chung. Vì chúng ta muốn mô hình học được cả mối quan hệ không loại trừ lẫn nhau nhằm tăng cường thông tin biểu diễn chứ không chỉ nhấn mạnh vào thông tin đáng chú ý và ít chú ý những gì nó không quan tâm. Do đó hàm sigmoid hợp lý hơn vì nó không giới hạn tổng các trọng số phải bằng 1 như softmax nên sẽ khiến mô hình học được cả thông tin loại trừ lẫn nhau.

2. Triển khai với thư viện Torch

Mô hình SE có thể dễ dàng tích hợp vào các kiến trúc hiện tại từ đơn giản như VGGNet cho đến mô hình đa nhánh phức tạp hơn như ResNet, EfficienetNet, .... Trong bài báo Squeeze-and-Excitation Network, tác giả có ví dụ mô đun SE gồm các lớp sau đây : Global pooling, Fully connected, Relu, Fully connected, Sigmoid như sau:

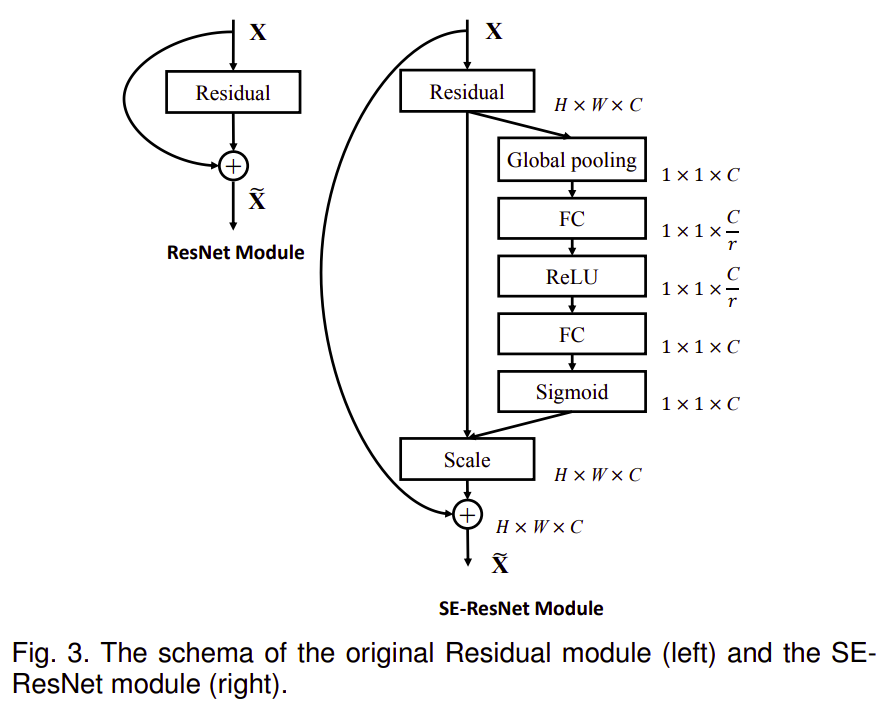
Và đây là phần code bằng pytorch tương ứng khá đơn giản đúng không nào

import torch
import torch.nn as nn
import torch.nn.functional as F

#   https://openaccess.thecvf.com/content_cvpr_2018/html/Hu_Squeeze-and-Excitation_Networks_CVPR_2018_paper.html

class SEBlock(nn.Module):

    def __init__(self, input_channels, internal_neurons):
        super(SEBlock, self).__init__()
        self.down = nn.Conv2d(in_channels=input_channels, out_channels=internal_neurons, kernel_size=1, stride=1, bias=True)
        self.up = nn.Conv2d(in_channels=internal_neurons, out_channels=input_channels, kernel_size=1, stride=1, bias=True)
        self.input_channels = input_channels

    def forward(self, inputs):
        # squeeze function
        x = F.avg_pool2d(inputs, kernel_size=inputs.size(3))
       
       # excitation function
        x = self.down(x)
        x = F.relu(x)
        x = self.up(x)
        x = torch.sigmoid(x)
        x = x.view(-1, self.input_channels, 1, 1)
        
        return inputs * x

Hiện tại trong bài viết lần này, mình sẽ chưa đưa ví dụ về mô hình SE trong một bài toán cụ thể mà mình sẽ giới thiệu cho các bạn vào một bài viết sắp tới kết hợp với mô hình RepVGG đang gây sốt hiện nay. Cảm ơn các bạn đã theo dõi bài viết của mình. (love)

Tài liệu tham khảo

Paper Squeeze-and-Excitation Network

Squeeze-and-Excitation Network Deep Learning