Tower of Hanoi

Bài đăng này đã không được cập nhật trong 3 năm

Background

Tower of Hanoi is a popular topic to study the recursion based algorithm. Basically, it's a mathematical game/puzzle was invented by the French mathematician Édouard Lucas in 1883.

According to the wikipedia note there is a story about a temple containing a large room with 03 towers are surrounded by 64 golden disks in a place of India namely Kashi Vishwanath. According to the story, the Brahmin priests were abiding by the command of an ancient prediction to move these 64 disks from source tower to destination tower. The principle rule is they could move one disk at a time and could't place a larger disk on top of a smaller one. It's said that if the last move of the puzzle would be completed, the world would be dead! Anyway, there are many variations in this story.

However, it's not clear that how Édouard Lucas invented this legend or was inspired by it. The temple may be said to be in different parts of the world including Hanoi, Vietnam which is may be associated with any religion.

The Tower of Hanoi also called as Tower of Brahma or Lucas Tower.

The Problem

According to the historical puzzle, in the modern computer science there is a recursion problem where you are given 03 pegs/towers and N disks with increasingly different sizes.

Let's name the towers as Tower-1, Tower-2 & Tower-3. Also, let's the number the disks from the smallest disk to the largest disk serially. At the scene, all disks are on Tower-1 in order of decreasing size from bottom to top, so that disk-N (the largest) is on the bottom and disk-1 (the smallest) is on the top. This is how one Tower of Hanoi can be made.

Here is an example below:

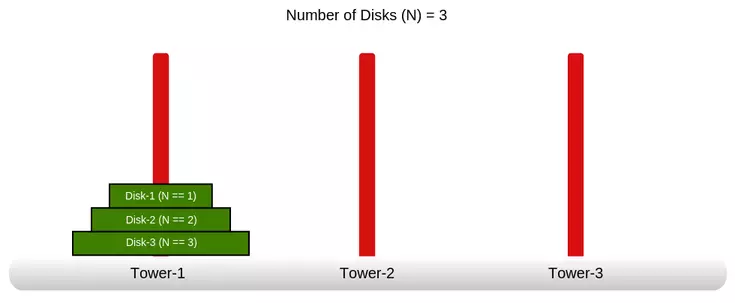
The basic outline of the problem is to move the N-number disks from the Tower-1, to the Tower-3, using the Tower-2 as the following rules:

In one time, one disk can be moved to any tower.
No big disk can't be placed upon on a small disk.

The Iterative Solution

According to the simple iterative solution we usually solve the puzzle as following:

(When the number of disks is even)

Move disk in-between Tower-1 and Tower-2
Move disk in-between Tower-1 and Tower-3
Move disk in-between Tower-2 and Tower-3
Repeat until complete

(When the number of disks is odd)

Move disk in-between Tower-1 and Tower-3
Move disk in-between Tower-1 and Tower-2
Move disk in-between Tower-3 and Tower-2
Repeat until complete

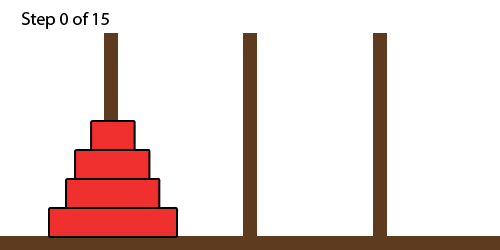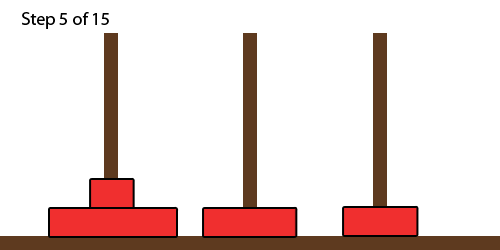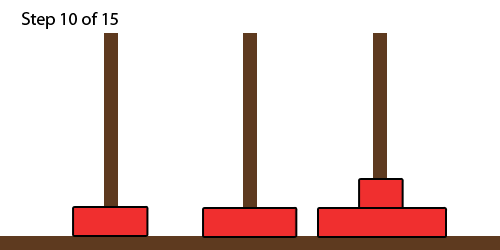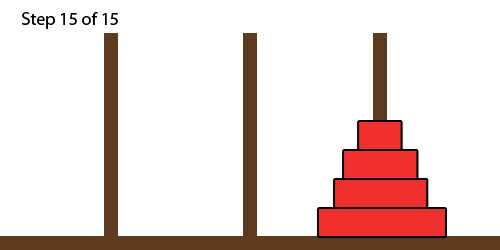
For example, there are the 15 steps are shown with (N=) 4 disks below:

The Recursive Solution

This is an interesting problem to solve in recursive strategy by breaking the large task into small tasks. Assuming that, our source is Tower-1, destination is Tower-3 & Tower-2 is the intermediary tower as usual. Therefore, for a given number (N) of disks, we have to follow the tasks below:

Move the top (N - 1) disks from Tower-1 to Tower-2 (using Tower-3 as an intermediary tower)
Move the bottom disk from Tower-1 to Tower-3
Move (N - 1) disks from Tower-2 to Tower-3 (using Tower-1 as an intermediary tower)

Let a function namely towerOfHanoi with four arguments (number of disks, source, destination & intermediary). Then the function will be like following:

towerOfHanoi(N, Tower1, Tower3, Tower2) {
    if N is 0
      return
    else
      towerOfHanoi(N - 1, Tower1, Tower2, Tower3)
      Move from Tower1 to Tower3
      towerOfHanoi(N - 1, Tower2, Tower3, Tower1)
 }

The above function is recursive because it calls itself repeatedly with decreasing values of N until the condition has been met.

For example, When N = 3:

Move from Tower1 to Tower3
Move from Tower1 to Tower2
Move from Tower3 to Tower2
Move from Tower1 to Tower3
Move from Tower2 to Tower1
Move from Tower2 to Tower3
Move from Tower1 to Tower3

Here is a C program using the above pseudocode is written below:

#include <stdio.h>

// tower1 = source
// tower2 = intermediary
// tower3 = destination
void towerOfHanoi(int n, char tower1, char tower3, char tower2) {
	if (n == 1) {
		printf("\n Move disk 1 from tower %c to tower %c", tower1, tower3);
		return;
	}
	towerOfHanoi(n-1, tower1, tower2, tower3);
	printf("\n Move disk %d from tower %c to tower %c", n, tower1, tower3);
	towerOfHanoi(n-1, tower2, tower3, tower1);
}

int main() {
	int n = 3; // number of disks
	towerOfHanoi(n, 'A', 'C', 'B'); // A, B and C are names of towers
	return 0;
}

Using the mathematical induction, it is cleared that the above procedure requires the minimal number of moves for the N-disks.