Tim Sort

Sorting data efficiently and rapidly is one of the hot talk among the computer science engineers. Several effective algorithms are created to do so, yet more research are undergoing to reach the linear time mark. Today our discussion will be on Timsort, a not very well-known algorithm, is called the fastest algorithm in the world that you never hear about.

Tim Sort

Timsort is a mixed and efficient sorting algorithm which is produced using the concept of both merge sort and insertion sort. Morever, It is designed to perform well on many kinds of real-world data. However, it is one of the few sorting algorithms which did not come out from school rooms. It was implemented by Tim Peters in 2002 for use in the Python programming language. The algorithm searches consequence of the data that are already in order and uses this result to sort the remainder more efficiently. This sorting is default sort in python programming language. in python version >=2.3, only sort(array) will apply tim sort on the data. Although the focus to develop this was only on python language, it is extensively used in other platform too, such as, JAVA, ANDROID, Google Chrome etc.

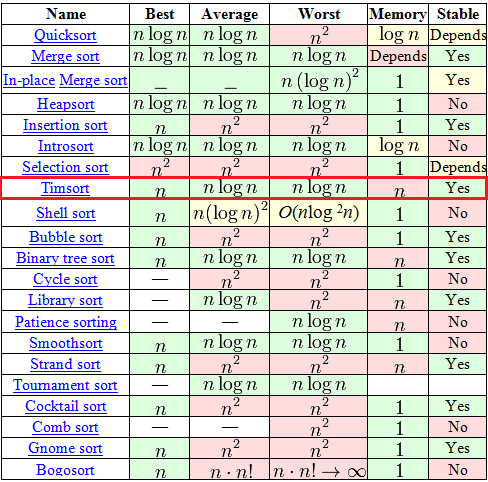
Importance

Glancing at the above image, we can analyse the note-worthy facts. At its best, Tim Sort overpowers Merge Sort and Quick Sort. At its worst, it runs at a parralel time with Merge Sort while outclassing Quick Sort. To be more precise, Its execution time is accurately fast. On the other hand, Tim Sort is on the black end of the spectrum in terms of space. Although O(n) is not that much harsh, but this is the case where receives a demerit point than quicksort. The last term for comparing algorithms is stability, which do not get much attention than speed and space. Stability is a very important factor in sorting. Maintaing the order of equal elements can give more reliance about the accuracy of a big result. Though quick sort is not stable all the time, Tim Sort is stable. Stability is one of the point where tim sort gets higher point despite it is little heavyweight than quicksort.

Algorithm steps

The main point of implementation is the use of runs. First we need to set a size which we will call minrun. What we need to realise by this is that we want to ensure that all our runs are at least a certain size. Initially we start with a run and we keep it for later use. When we find the longest run within a minrun range. We now have a small, sorted array. If it is at least minrun in length, then we are ready to start. Otherwise we have to get insertion sort in action. If it isn’t at least minrun in length, we go ahead and find enough other elements to complete the run and thus use Insertion Sort to push them into our sorted array simply. Obviously, if a run reaches the end of the array we can let it be a little short. Once we have created all the runs, we need to utilize Merge Sort to join them together. In a best case scenario the entire array is already sorted and Tim Sort is smart enough to know it doesn’t need to do anything else. Other times, it tends to just be extremely efficient. As an added benefit, both Insertion Sort and Merge Sort are stable, so the resulting array is stable.

In small talk, we can write the steps:

• Build a minrun of size less than 64. Usually we need to take a number which is a power of 2. For simplycity we often take 32.
• Search for a run in the first minrun of data.
• If we unable to find a run of at least minrun in length, we need to use Insertion Sort to get subsequent items and push them into the run until it is the correct size.
• We need to repeat until the entire array is divided into sorted subsections.
• Now we need to use Merge Sort to join the ordered arrays.

Implementation

Below is the ruby implementation of tim sort. In this implementation, I am skipping the implementation of merge sort and quick sort. If you need some more info about them, google is always there to serve you.

def timSort arr
  counter = 0
  no_of_element = arr.count

  while counter < no_of_element do
    insertionSort arr, counter, [(counter+31), (no_of_element-1)].min
    counter += 32
  end

  size = 32

  while size < no_of_element do
    left = 0

    while left < n do
      mid = left + size - 1
      right = [(left + 2*size - 1), (n-1)].min 

      merge arr, left, mid, right
      left = 2 * size
    end
    
    size = 2 * size 
  end 
end

Tim sort is a very strong, rapid and powerful sorting algorithm which focuses mainly on real-world data. But you have to understand that it is not feasible for all the cases. So if you are interested more, tou need to study more to understand its usage.

Reference: https://en.wikipedia.org/wiki/Timsort