Hamiltonian path problem

This article aims to summarize the Hamiltonian path problem. Before getting start, let's revise few basic theories to know about the mesh graph.

Graph

A Graph (G) includes 02 sets V and E, where V is the set of vertices and E is the set of pairs of vertices called edges. An edge is said to be incident to the vertices if it joins. Graph G = (V , E) is called a simple graph if every pair of vertices has at most one edge that is incident to these two vertices and there is no loop (a, a) ∈ E for any a ∈ V.

You can find more details explanation about graph theory here to understand the theory as well.

Grid Graph

A grid (also known as mesh or lattice) graph denotes a drawing which is embedded in a Euclidean space like grid graph or triangular grid graph.

Grid (or, mesh) graphs are regular graphs, meaning that each edge has the same weight or represents the same distance in Euclidean space as in other spaces.

Hamiltonian path problem

The longest path problem is a well-known NP-complete Hamiltonian path problem, i.e. deciding whether there is a simple path that visits each vertex of the graph exactly once, is a special case of the longest path problem. The rectangular grid graph R(n, m) is the subgraph of G∞ (the infinite grid graph) induced by V(m, n)={υ|1≤ vx ≤m, 1 ≤vy ≤n}, where vx and vy are respectively x and y coordinates of v. The Hamiltonian path problem has been studied for grid graphs, where it's proved that the problem for general grid graphs is NP-complete. You can find a deep study where several theories are stated to explain the problem. The Hamiltonian path problem is noted as an algorithm as following.

As a complete example, the construction of a longest path between s and t in R(12, 5) is shown step by step below:

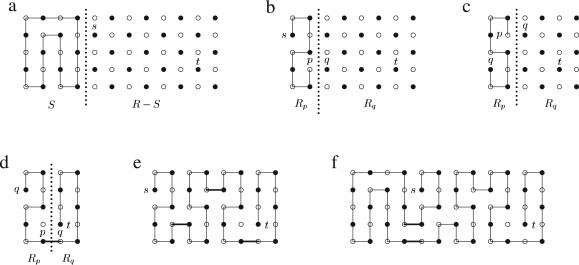
This is a linear-time algorithm in a rectangular grid graph between any two given vertices.