Reinforcement Learning: Q-Learning

Introduction

Trong một vài năm trở lại đây, chúng ta đã có những bước tiến dài cùng với các mô hình Deep Learning. Các mô hình này đã giúp chúng ta thực hiện được những công việc tưởng chừng như là không thể trước đây. Tuy nhiên, theo ý kiến cá nhân mình thấy, dường như lĩnh vực này đang dần chạm tới mốc bão hòa. Và thay vào đó, sự chú ý của giới công nghệ đang dần chuyển sang Reinforcement Learning (RL). Vậy trong bài viết này chúng ta hãy cùng đi tìm hiểu về RL và đặc biệt là mô hình Q-Learning nhé. Let's go!!!!

Reinforcement Learning

Trong RL, máy sẽ học cách thực hiện nhiệm vụ bằng cách tương tác với môi trường thông qua các hành động và dựa trên phần thưởng qua từng hành động mà đưa ra lựa chọn tối ưu. Cách xây dựng của thuật toán này khá giống với cách mà con người chúng ta học, qua thử nghiệm và sai lầm.

Dưới đây là một sơ đồ mô tả cách hoạt động của RL, nhưng trước khi đi vào giải thích kĩ hơn, chúng ta hãy cùng làm quen với một số thuật ngữ được sử dụng ở đây:

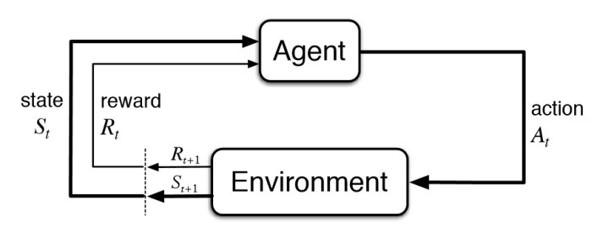
• Environment (Môi trường): là không gian mà máy tương tác
• Agent (Máy): là chủ thể tương tác với môi trường qua hành động
• Policy (Chiến thuật): là chiến thuật mà máy sử dụng để đưa ra hành động
• State (Trạng thái): mô tả trạng thái hiện tại của máy
• Reward (Phần thưởng): phần thưởng từ môi trường tương ứng với hành động được thực hiện
• Action (Hành động): là những gì máy có thể thực hiện

Chúng ta sẽ bắt đầu từ state S(t), tại trạng thái này, agent sẽ dựa trên policy đã được thiết kế sẵn để đưa ra một action A(t) trong environment. Environment sau khi quan sát hành động sẽ chuyển đổi sang trạng thái tiếp theo S(t+1) đối với agent và đồng thời dựa theo hành động mà agent đã thực hiện, environment sẽ đưa ra phần thưởng R(t) tương ứng. Agent sẽ lặp đi lặp lại qui trình này cho đến khi tìm được chuỗi những hành động tối đa hóa phần thưởng được nhận.

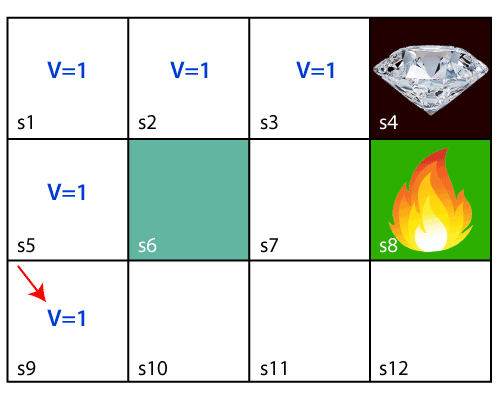
Giả sử rằng chúng ta có một trò chơi đơn giản minh họa bởi ảnh phía trên với mục tiêu là lấy được viên kim cương, agent sẽ bắt đầu từ ô s9, vậy một giải pháp đơn giản chúng ta có thể thấy là agent sẽ di chuyển lần lượt qua các ô s5-s1-s2-s3 để tới được viên kim cương với quãng đường là ngắn nhất. Tuy nhiên, nếu agent được đặt tại vị trí s1, khi đó agent sẽ có 2 hướng đi với các giá trị như nhau. Vậy chúng ta làm thế nào để đảm bảo được agent sẽ thực hiện đúng những hành động tối ưu mà chúng ta muốn? Đó là tạo một memory (bộ nhớ) cho agent, sử dụng Bellman Equation. Dưới đây là công thức:

$$V(s) = \max_{\substack{a}} (R(s, a) + γV(s'))$$

Trong đó,

• s: Một state cụ thể
• a: Một action do agent thực hiện
• *s': Trạng thái trước đó *
• $\gamma$: Discount factor (chúng ta sẽ tìm hiểu bên dưới)
• R(s, a): Hàm số phần thưởng với biến là trạng thái s và hành động a và trả lại kết quả là giá trị của phần thưởng
• V(s): giá trị tại một trạng thái cụ thể

Vậy sau khi áp dụng Bellman Equation, ta có giá trị tại các state thay đổi như hình dưới đây. Chi tiết các bước tính toán xin xem tại đây.

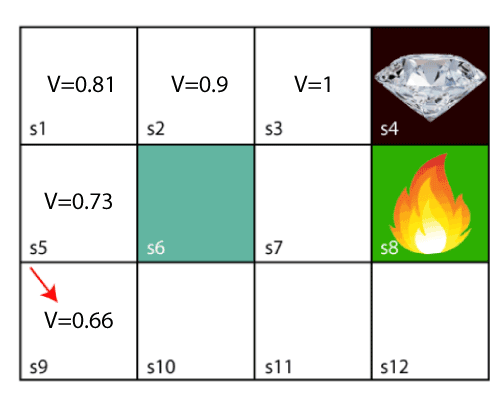
Hàm $\max$ giúp agent có thể tìm được chuỗi hành động tối ưu trong đó discount factor $\gamma$ giúp thông báo cho agent còn cách đích đến bao xa. Tuy nhiên, trong nhiều trường hợp phải đưa ra quyết định giữa nhiều lựa chọn, Bellman Equation vẫn có một tỉ lệ nhỏ khiến agent bị rối loạn. Vấn đề ở đây là quá trình đưa ra quyết định vừa ngẫu nhiên vừa trong tầm kiểm soát. Trong tầm kiểm soát vì agent vẫn tuân thủ những chiến lược chúng ta đã đặt ra tuy nhiên lại ngẫu nhiên vì chúng ta không biết khi nào thì agent sẽ rối loạn. Thế nhưng chúng ta có thể đưa concept này vào trong Bellman Equation với một số chỉnh sửa nhỏ:

$$V(s) = \max_{\substack{a}} (R(s, a) + \gamma \sum_{\substack{s'}} P(s, a, s') V(s'))$$

• P(s, a, s'): xác suất di chuyển từ trạng thái s sang s' với hành động a

Quá trình này được biết đến với cái tên Markov's Decision Process (MDP).

Bên trên là sơ lược những kiến thức chúng ta cần nắm được trước khi chuyển sang phần tiếp theo: Q-Learning

Q-Learning

Mô hình Q-Learning cũng gần giống với quá trình đã đưuọc đề cập ở trên. Tuy nhiên, thay vì dựa trên giá trị của các state V(s) mà đưa ra quyết định về hành động thì Q-Learning tập trung hơn vào việc đánh giá chất lượng của một hành động Q(s, a). Vậy chúng ta làm như nào để đánh giá được các hành động này? Từ bên trên chúng ta có công thức:

$V(s) = \max_{\substack{a}} (R(s, a) + \gamma \sum_{\substack{s'}} P(s, a, s') V(s'))$

Trong công thức này chúng ta đang quan tâm đến tất cả các state và tất cả các action khả thi. Vậy khi bỏ hàm $\max$, chúng ta sẽ được công thức $R(s, a) + \gamma \sum_{\substack{s'}} P(s, a, s') V(s')$ và hãy nghĩ nó như là giá trị của một state được tạo ra cho chỉ một hành động khả thi. Chúng ta sẽ lấy phương trình này làm phương trình đánh giá hành động Q(s, a) như sau:

$$Q(s, a) = R(s, a) + \gamma \sum_{\substack{s'}} P(s, a, s') V(s')$$

Để giảm thiểu các công việc tính toán đồng thời để tạo nên sự đồng nhất, chúng ta có thể tiến hành cải tiến công thức thêm một bước nữa:

$$Q(s, a) = R(s, a) + \gamma \sum_{\substack{s'}} P(s, a, s') \max_{\substack{a'}} Q(s', a')$$

Sỡ dĩ chúng ta thay V(s) bằng $\max Q(s, a)$ bởi ở đây, chúng ta coi giá trị của một state được tính bằng giá trị lớn nhất có thể của Q(s, a). Giá trị được tính toán từ công thức này được gọi là Q-values và agent sẽ học cách tự tính toán Q-values và đưa ra hành động dựa trên các giá trị này. Ở trên chúng ta đã hiểu agent đưa ra lựa chọn dựa trên Q-values như thế nào, vậy giờ hãy cùng đến với một phần cuối đó là cách để agent có thể tự tính toán Q-values.

Temporal Difference (TD)

Chúng ta đã biết môi trường không phải bất biến mà sẽ thay đổi theo thời gian, vậy phài làm như nào để nắm bắt được sự thay đổi của môi trường? Đơn giản thôi, đó chính là tính lại Q-values mới sử dụng công thức vừa xây dựng ở trên sau đó trừ đi Q-values đã biết.

$$TD(a, s) = \underbrace{R(s, a) + \gamma \sum_{\substack{s'}} P(s, a, s') \max_{\substack{a'}} Q(s', a')}_{\text{new Q-value}} -Q(s, a)$$

Phương trình trên cho thấy một sự thay đổi tạm thời của môi trường dựa theo Q-values. Vậy việc chúng ta cần làm là update các Q-values mới sử dụng công thức:

$$Q_{\substack{t}}(s, a) = Q_{\substack{t-1}}(s, a) + \alpha TD_{\substack{t}}(s, a)$$

Trong đó,

• $\alpha$: là tốc độ học (learning rate) tượng trưng cho việc agent thích nghi nhanh chóng như thế nào với sự thay đổi của môi trường
• $Q_{\substack{t}}(s, a)$: là Q-value hiện tại
• $Q_{\substack{t-1}}(s, a)$: là Q-value trước đó

Và đến đây là đã đầy đủ kiến thức cần biết để chúng ta có thể xây dựng một mô hình Q-Learning cho riêng mình rồi. Cảm ơn đã đọc và hẹn gặp lại các bạn ở các bài viết sau!