Spatial Transformation trong Adversarial ML

Introduction

Từ trước đến nay, khi nhắc đến adversarial examples, chúng ta đều thường nghĩ đến những chiến lược tấn công dựa trên $L_{\substack{2}}$ hoặc $L_{\substack{\infin}}$. Tuy nhiên, đây chưa hẳn là một thước đo lí tưởng bởi $L_{\substack{2}}$ thường rất nhạy cảm với những tác nhân như ánh sáng của ảnh, v..v... Chẳng hạn như chúng ta dịch cả ảnh tăng lên 1 pixel cũng có thể tạo nên sự thay đổi lớn cho $L_{\substack{2}}$. Bởi vậy nên chúng ta cần có một hướng đi mới, và xin giới thiệu Spatially Transformed Adversarial Examples hay tạm gọi là biến dạng hình ảnh.

Related Work

Adversarial Examples: Trong một mô hình phân loại ảnh (image classification), với mỗi một ảnh đưa qua mô hình (sample x), nếu chúng ta thêm vào đó một sự "nhiễu loạn" nhỏ (noise/perturbation), mặc dù đối với nhận thức của con người thì bức ảnh không hề xuất hiện một sự thay đổi nào nhưng khi đưa qua mô hình phân loại, máy sẽ trả lại kết quả không chính xác so với kết quả ban đầu. Dưới đây là ví dụ một bức ảnh được phân loại là "Pig", nhưng sau khi thêm noise đã làm cho mô hình phân loại sai thành "Airliner" (tìm hiểu thêm tại đây)

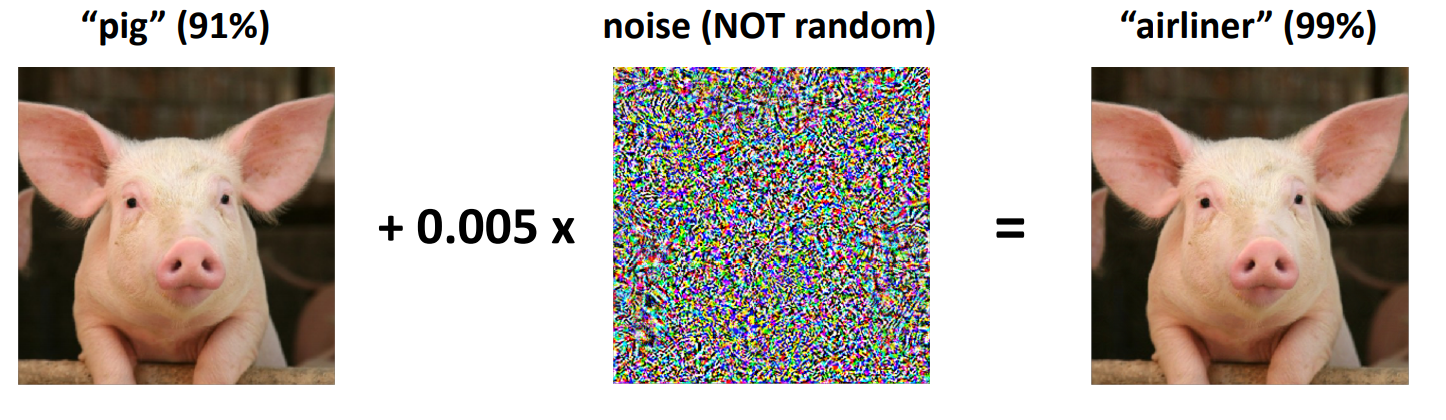
Vậy những sample khiến cho mô hình đã được trained phân loại nhầm được gọi là adversarial examples, kí hiệu là $x_{\substack{adv}}$ ($x_{\substack{adv}} = x + \epsilon$, với $\epsilon$ là noise đã nói ở trên)

Defensive method: Việc lợi dụng adversarial example để khiến mô hình đưa ra phán đoán sai lệch được gọi là adversarial attacks và để đảm bảo cho các mô hình khi sử dụng có khả năng kháng lại những sự tấn công từ adversarial example thì những defensive methods đã được ra đời. Có thể kể đến các phương pháp như adversarial training, distilllation, feature squeezing, ensemble và hơn nữa.

Tạo Adversarial Examples

Pixel-based Attacks:

• Fast Gradient Sign Method: là một phương thức tấn công bậc nhất đơn giản sử dụng gradient ascent để tạo nên adversarial example sử dụng công thức:

$$x_{\substack{adv}} = x + \epsilon sign(∇_{\substack{x}} l_{\substack{g}}(x, y))$$

Trong đó, $l_{\substack{g}}(x, y)$ là hàm mất mát được sử dụng để huấn luyện mô hình g, y là nhãn đúng và $\epsilon$ điều khiển perturbation được thêm vào ảnh.

• C&W: tạo nên adversarial examples có chủ đích (targeted) dựa trên một số ràng buộc được thể hiện qua công thức:

$$min ||δ|| _{\substack{p}}^2 \qquad s.t. \qquad g(x + δ) = t \quad and \quad x + δ ∈ X$$

Trong đó, $L_{\substack{p}}$ được sử dụng để đảm bảo rằng $\epsilon$ nhỏ. Công thức có thể được thay đổi với $g(x + δ) \mathrlap{\,/}{=} y$ cho các adversarial examples không có chủ đích (untargeted).

Spatial Transformation Attack:

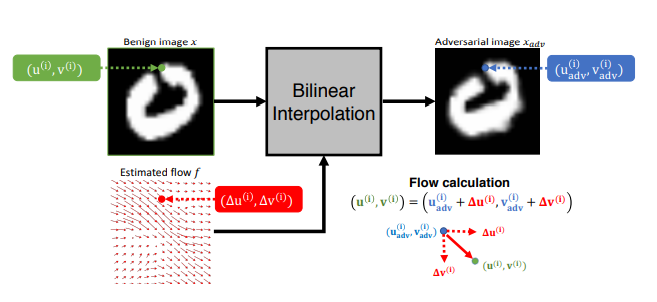
Sở dĩ gọi là phương pháp "biến đổi không gian" là bởi thay vì chúng ta trực tiếp thay đổi giá trị pixel như ở các phương pháp tấn công trước kia, thì giờ một trường chuyển dời (flow field) f sẽ được tạo nên. Có thể hiểu trường f sẽ chứa các véc-tơ giúp xác định hướng biến đổi của các pixels trong ảnh.

Một bức ảnh sẽ được biểu diễn dưới dạng một ma trận khi cho vào mô hình, vậy mỗi vị trí của một pixel sẽ được biểu diễn qua (u, v). Một adversarial examples $x_{\substack{adv}}$ tại vị trí ith pixel sẽ được kí hiệu $x^i_{\substack{adv}} = (u^i_{\substack{adv}}, v^i_{\substack{adv}})$. Tại đây, chúng ta sẽ tối ưu hóa một véc-tơ chuyển dời $f_{\substack{i}} := \ (\Delta u^i, \Delta v^i)$, véc-tơ này có chiều đi từ ith pixel của $x_{\substack{adv}}$ đến ith pixel của $x$ vì vậy chúng ta có sự biểu diễn $(u^i, v^i) = (u^i_{\substack{adv}} + \Delta u^i, v^i_{\substack{adv}} + \Delta v^i)$. Sử dụng differentiable bilinear interpolation, công thức mới dưới đây sẽ được tạo ra để biến đổi ảnh đầu vào $x^i_{\substack{adv}}$

$$x^i_{\substack{adv}} = \sum_{\substack{q \in N(u^i, v^i)}} x^q (1 - |u^i - u^q|)(1 - |v^i - v^q|)$$

Trong đó, tập $N(u^i, v^i)$ là tập hợp các tọa độ của các pixels trên, dưới, trái, phải của pixel $(u^i, v^i)$. Áp dụng công thức trên với i là toàn bộ các pixels của ảnh ta sẽ thu được $x_{\substack{adv}}$.

Các phương pháp tấn công trước đây đều bị giới hạn lượng perturbation được thêm vào ảnh dựa trên $L_{\substack{p}}$, tuy nhiên phương pháp tấn công mới này sẽ đưa ra một khái niệm hàm regularization loss mới $L_{\substack{f}}$. Từ đó, mục tiêu của phương pháp tấn công mới trở thành tạo nên các adversarial examples có thể đánh lừa được mô hình đồng thời tối thiểu hóa sự bóp méo của hình ảnh đến từ trường chuyển dời (flow field) f. Vậy trường chuyển dời (flow field) được tính như thế nào?

$$f^* = \argmin_{\substack{f}} \quad L_{\substack{adv}}(x, f) + \tau L_{\substack{f}}(f)$$

Trong đó, hàm $L_{\substack{adv}}$ khuyến khích sự lệch nhãn khi đưa adversarial example vào mô hình, hàm $L_{\substack{f}}$ giảm thiểu sự bóp méo hình ảnh để vẫn giữ nguyên được đa phần hình dạng ban đầu để không dẫn tới sự sai lệch nhận thức và biến số $\tau$ giúp cân bằng giữa 2 hàm mất mát này

Ngoài ra, trong tấn công có chủ đích (targeted attack), hàm $L_{\substack{adv}}$ còn đóng vai trò đảm bảo rằng $g(x_{\substack{adv}}) = t$ với $g$ là mô hình đang sử dụng và $t$ là nhãn chúng ta đang hướng tới, khác với nhãn đúng $y$. Để làm được vậy, chúng ta sẽ áp dụng tương tự phương pháp tấn công C&W đã được nhắc đến ở trên:

$$L_{\substack{adv}}(x, f) = \max (\max_{\substack{i \not = t}} g(x_{\substack{adv}})_{\substack{i}} - g(x_{\substack{adv}})_{\substack{t}}, \kappa)$$

$g(x)$ là biểu diễn cho véc-tơ output của mô hình $g$ đang sử dụng, $g(x)_{\substack{i}}$ chỉ thành phần thứ $i$ của véc-tơ và $\kappa$ tượng trưng cho confidence level.

Về hàm $L_{\substack{f}}$, hàm này sẽ được tính bằng cách tính tổng khoảng cách dịch chuyển của của 2 pixels bất kì cạnh nhau. Có thể dễ dàng hình dung được rằng khi hàm nay được tối thiểu hóa, sự bóp méo hình ảnh cũng được giảm xuống mức thấp nhất, giữ được đa phần hình ảnh gốc vì các pixels kề nhau thường có xu hướng di chuyển theo hướng và khoảng cách gần. Chúng ta có công thức:

$$L_{\substack{f}}(f) = \displaystyle\sum_{i=1}^\text{\scriptsize $all \ pixels$} \sum_{\substack{q \in N(p)}} \sqrt{\| \Delta u^p - \Delta u^q \|^2_{\substack{2}} + \| \Delta v^p - \Delta v^q \|^2_{\substack{2}}}$$

trong đó $p$ là một pixel trong ảnh và $q \in N(p)$ là các pixels kề cạnh pixel $p$.

Kết quả thực nghiệm

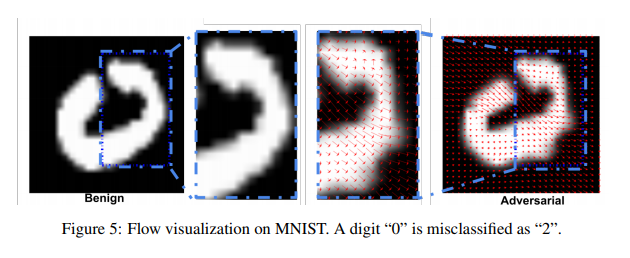
Ảnh và kết quả được lấy tại đây.

Quan điểm cá nhân

Đây là một phương pháp tấn công mới, cho thấy các mô hình hiện tại của chúng ta tuy rằng đã cho thấy những kết quả rất tốt nhưng vẫn còn tồn tại những lỗ hổng và thiếu sót. Và cũng mở ra một hướng nghiên cứu mới về an ninh mô hình khi phương pháp này không đi theo những lối mòn của các phương án trước kia sử dụng $L_{\substack{p}}-norm$ để tạo adversarial examples