Sơ lược về Maximum Likelihood Estimation
Bài đăng này đã không được cập nhật trong 6 năm
1. Statistical Machine Learning
Đối với một bài toán Machine Learning tổng quát, việc giải quyết bài toán thường gồm 3 bước chính:
- Modeling: Đi tìm mô hình có thể mô tả tốt nhất bài toán
- Learning: Tối ưu tham số cho mô hình dựa vào dữ liệu có sẵn
- Inference: Sử dụng mô hình đã tối ưu để dự đoán kết quả với đầu vào chưa biết
Trong Statistical Machine Learning (Học máy Thống kê), mô hình bài toán thường là sự kết hợp của các phân phối xác suất đơn giản (Bernoulli, Gaussian, …). Ở bước Learning, có hai phương pháp được sử dụng phổ biến để tối ưu bộ tham số, đó là Maximum Likelihood Estimation và Maximum A Posteriori Estimation.
Trong bài viết này, chúng ta cùng tìm hiểu phương pháp Maximum Likelihood Estimation thông qua ví dụ đơn giản. Phương pháp Maximum A Posteriori Estimation sẽ được giới thiệu trong phần tiếp theo.
2. Maximum Likelihood Estimation (MLE)
MLE là phương pháp dự đoán tham số của một mô hình thống kê dựa trên những “quan sát” có sẵn, bằng cách tìm bộ tham số sao cho có thể tối đa hoá khả năng mà mô hình với bộ tham số đó sinh ra các “quan sát” có sẵn.
Giả sử mô hình được mô tả bởi bộ tham số θ, các “quan sát” (hay điểm dữ liệu) là x1, x2, …, xN. Khi đó chúng ta cần tìm:
θ = argmax{ p(x1,x2,…,xN|θ) } (1)
, trong đó: p(x1,x2,…,xN|θ) là xác suất để các sự kiện x1, x2, …, xN xảy ra đồng thời, được gọi là likelihood. Chính vì vậy mà phương pháp này được gọi là Maximum Likelihood.
Tuy nhiên, việc giải trực tiếp bài toán (1) thường là khó khăn. Chúng ta có thể đơn giản hoá bài toán bằng việc giả sử các điểm dữ liệu xảy ra độc lập với nhau. Khi đó, (1) trở thành:
θ = argmax{ p(xn|θ) } (2)
Chúng ta có thể khiến việc tính toán dễ dàng hơn bằng cách biến đổi về bài toán Maximum Log-likelihood:
θ = argmax{ log(p(xn|θ)) } (3)
3. Ví dụ
Để hiểu rõ hơn về MLE, chúng ta cùng làm một ví dụ đơn giản.
Giả sử bài toán là có 5 học sinh làm bài kiểm tra được số điểm lần lượt là: 3, 6, 5, 9, 8. Để mô hình hoá điểm của các học sinh này, ta giả thiết các điểm dữ liệu được phân bố theo phân phối Gaussian:
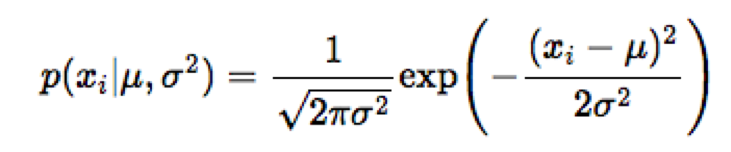
Để dự đoán bộ tham số của phân phối chuẩn, ta sử dụng phương pháp MLE:
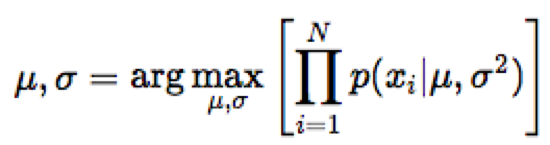
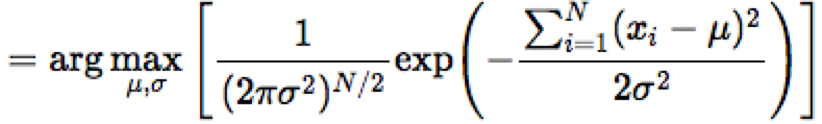
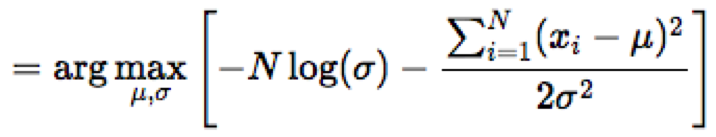
Để tìm μ và σ sao cho biểu thức trong ngoặc vuông đạt giá trị cực đại, chúng ta đạo hàm biểu thức theo từng biến và giải phương trình khi giá trị đó bằng 0.
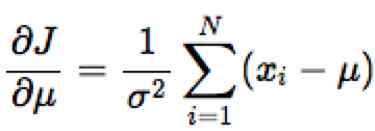
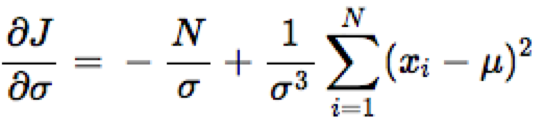
Từ đó ta có:
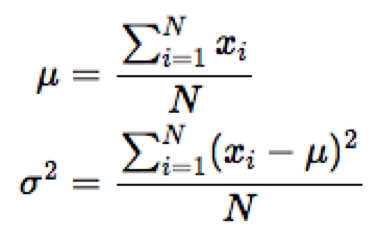
Thay các điểm dữ liệu vào công thức trên, ta tìm được μ = 6.2 và σ = 2.14.
4. Kết luận
Hy vọng qua bài viết này, các bạn đã hiểu rõ hơn về phương pháp Maximum Likelihood Estimation. Trong phần tiếp theo, chúng ta sẽ tìm hiểu về phương pháp tổng quát hơn là Maximum A Posteriori Estimation.
5. Tài liệu tham khảo và Nguồn hình ảnh
All rights reserved