Mở đầu

Ở bài viết lần trước, mình đã trình bày sơ qua các kiến thức các bạn sẽ gặp phải trong YOLOv7, nếu muốn các bạn có thể đọc lại ở đây: https://viblo.asia/p/paper-explain-yolov7-su-dung-cac-trainable-bag-of-freebies-dua-yolo-len-mot-tam-cao-moi-phan-1-zXRJ8BGOVGq.
Ở phần 1, mình có nhắc tới khái niệm Label Assignment và đã giải thích sơ qua. Tuy nhiên, đối với các model Object Detection thời hiện đại (từ nửa sau 2020 trở đi), thì Label Assignment trở thành một vấn đề cực kì quan trọng. Các thành phần khác của YOLOv7 (ngoài backbone ELAN) thì không có gì quá mới mẻ và có thể đã quen thuộc với nhiều người như: Model Scaling, RepVGG Block,... Riêng Label Assignment thì ảnh hưởng tới tận 2 thay đổi thực hiện trong YOLOv7, nên mình quyết định sẽ phân tích kĩ về Label Assignment tại phần 2 này.

Label Assignment (LA)

Ở phần trước, mình đã giới thiệu sơ qua Label Assignment (LA) nghĩa là gì. Có lẽ vẫn sẽ còn nhiều người thắc mắc positive/negative sample là gì. Cùng đi ngược lại YOLOv1 một chút nhé. YOLOv1, cụ tổ của YOLO, là phiên bản duy nhất không sử dụng đến Anchor Box từ YOLOv1-YOLOv5. Nhìn lại hàm loss của YOLOv1, ta sẽ thấy tất cả các hàm loss đều có một tham số phụ $1^{obj}$ hay $1^{noobj}$, với $1^{obj}$ đại diện cho cell có tồn tại object và ngược lại với $1^{noobj}$. Các cell có tồn tại object này sẽ được gọi là positive samples và các cell không tồn tại object sẽ được gọi là negative samples. Lúc này, việc định nghĩa positive/negative samples sẽ là quá trình đi gán cell nào là cell tồn tại object, cell nào là cell không tồn tại object. Việc này sẽ ảnh hưởng trực tiếp tới hàm loss của model, do đó, ảnh hưởng tới hiệu năng của model.

Nhưng YOLOv1 thì đã quá là lạc hậu và có những thứ không phù hợp, không áp dụng được với các model Object Detection bây giờ. Để hiểu rõ hơn về Label Assignment và điểm khác nhau giữa Anchor-based và Anchor-free, mình sẽ đưa các bạn quay về RetinaNet (Anchor-based Object Detection model) và FCOS (Anchor-free Object Detection model). Trong YOLOv1, ở feature map cuối cùng có kích cỡ $7 \times 7$ dùng để đưa ra prediction, YOLOv1 sẽ thực hiện predict tâm của Bounding Box $(cx, cy)$ và chiều dài, rộng của Bounding Box $(w, h)$ khi cell đó được cho là positive sample. Tuy nhiên, trong FCOS, ta sẽ predict giới hạn của Bounding Box. FCOS sẽ từ một điểm trung tâm của một cell, predict khoảng cách từ điểm trung tâm của cell đó đến 4 cạnh của Bounding Box $(l, t, r, b)$ khi điểm trung tâm đó được cho là positive sample. Còn khi predict Box thì RetinaNet thực hiện predict như từ YOLOv2 trở đi, vì cùng là Anchor-based.

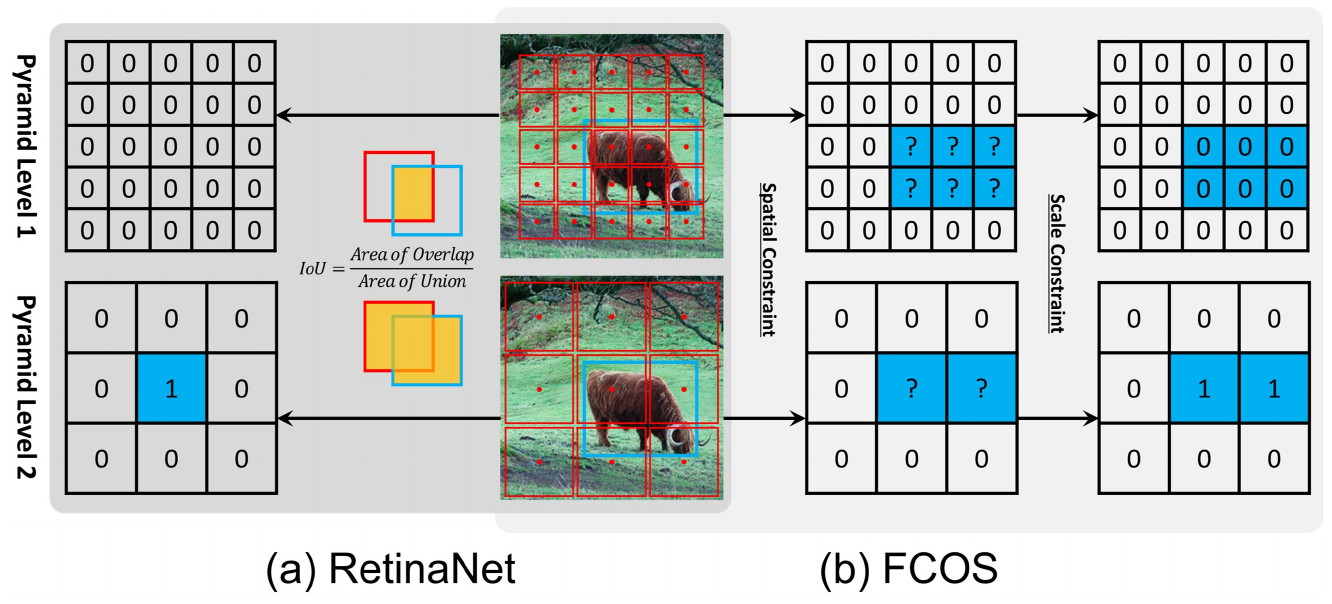
Để cho thuận tiện trong việc gọi tên, thì mình sẽ gọi luôn điểm trung tâm của một cell được sử dụng trong FCOS là anchor. Anchor trong các phương pháp Anchor-free là anchor point, còn anchor trong các phương pháp Anchor-based là anchor box, nên từ giờ mong các bạn sẽ chú ý đến ngữ cảnh khi mình sử dụng từ anchor. Có 3 điểm khác nhau chính giữa FCOS và RetinaNet:

• Số lương anchors được đính trong một cell: Như đã biết, Anchor-based sử dụng tới 9 anchors (với 3 kích cỡ và 3 hình dạng khác nhau) cho một cell. Còn với Anchor-free, điểm trung tâm của một cell thì chỉ có một mà thôi, làm gì có hình vuông nào mà có tới tận 2 cái điểm trung tâm.
• RetinaNet sử dụng IoU để xác định xem anchor nào là positive anchor, đây là chiến thuật Label Assignment của RetinaNet. Nếu chưa rõ về cách chọn positive anchor sử dụng IoU, mời các bạn đọc lại bài phân tích YOLOv2 của mình ở đây. Còn FCOS sử dụng giới hạn về scale và kích cỡ (Hình 1). Về chi tiết, mình khuyến khích các bạn nên đọc phần 3.2 trong paper FCOS để hiểu rõ được. Còn nếu có thắc mắc thì hãy comment xuống phía dưới để mình giải thích kĩ hơn.
• Cách predict ra box (Hình 2): RetinaNet predict Box dựa trên độ lệch giữa Anchor Box và Bounding Box. Còn FCOS predict Box dựa trên khoảng cách từ anchor tới 4 cạnh như mình đã nói ở trên.

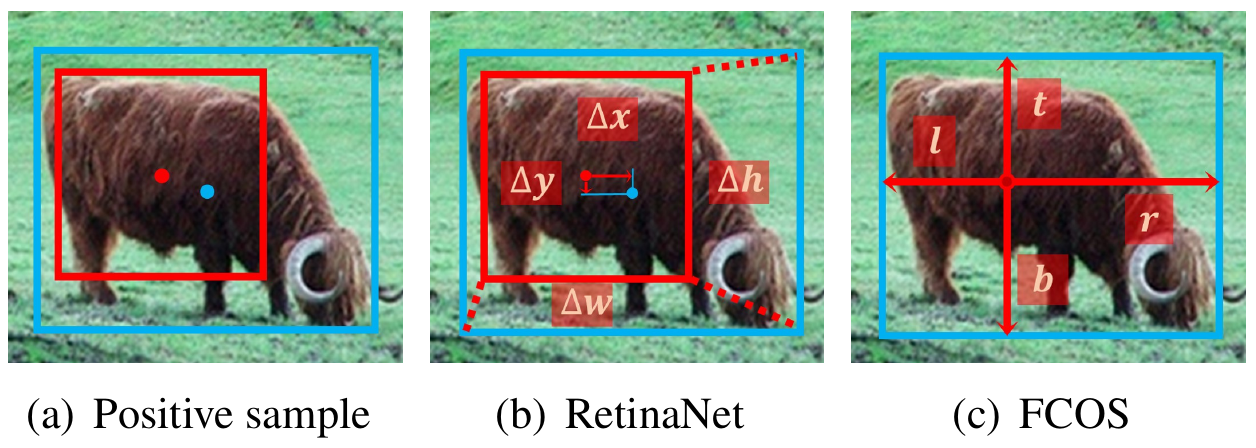
Hy vọng là với phần giải thích phía trên, các bạn đã hiểu kĩ hơn về positive/negative samples, LA là làm gì và sự khác nhau giữa Anchor-based và Anchor-free model.

OTA và SimOTA

YOLOv7 sử dụng LA là SimOTA (Simple OTA), chiến thuật LA được sử dụng trong YOLOX, là phiên bản đơn giản hơn của OTA. Ở phía dưới, mình sẽ phân tích về OTA và sau đó đi vào SimOTA.

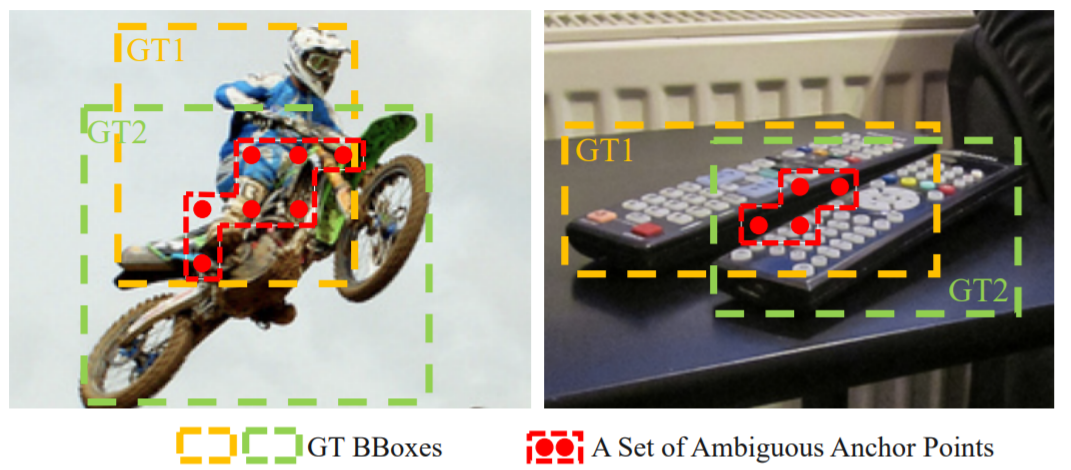
Trước tiên, ta phải hiểu, LA của FCOS có gì chưa tốt?

• Vẫn còn phải sử dụng các hyper-params: FCOS đề ra các hyper-params là giới hạn về scale và kích cỡ để chọn positive samples ứng với từng scale của FPN.
• Chưa giải quyết được các trường hợp anchors "ambigous" (không rõ ràng - Hình 3): Một anchors được cho là ambigous khi anchors đó thỏa mãn làm positive sample cho nhiều gt cùng 1 lúc. Như ở hình 3, các bạn có thể thấy gán các anchors được đánh dấu làm positive sample cho cả 2 gt box thì đều phù hợp cả. Nếu ta gán bừa những anchors này cho Background (BG) hay cho một object nào đó thì nó sẽ gây ảnh hưởng đến object khác, từ đó làm giảm hiệu suất của model.

Để khắc phục 2 nhược điểm kể trên, OTA muốn:

• Tự động chọn positive samples theo thuật toán chứ không phải phụ thuộc vào các hyper-params được định nghĩa trước (1)
• Số lượng positive samples cho từng object là khác nhau, vì mỗi object có kích cỡ, hình dạng khác nhau (2)
• Sử dụng Global View để chọn positive samples từ các ambiguous anchors (3)

LA là một bài toán Optimal Transport (OT)

Cảnh báo: Phần tiếp theo sẽ bao gồm rất nhiều toán, và thuật toán
OTA giải quyết đồng thời (1) và (3) nhắc tới bên trên bằng việc coi quá trình Label Assigment là một bài toán Optimal Transport, từ đó tạo ra cái tên OTA: Optimal Transport Assignment. Vậy OT là gì và nó giúp ích gì cho việc giải quyết (1) và (3)? (1) thì có vẻ dễ hiểu rồi, mình sẽ làm rõ Global View trong (3) là gì nhé. Với các chiến thuật LA đã từng được đề ra, chúng thất bại trong việc giải quyết ambiguous anchors vì chúng sử dụng các hyper-params (Min Area, Max IoU) hoặc Local View. Local View nghĩa là chúng tập trung LA tốt cho một object trong một ảnh mà không hề quan tâm tới các objects khác như nào, lần lượt thực hiện LA cho các object trong ảnh một cách độc lập với nhau. Chính vì chúng ta chỉ thực hiện LA từng object trong ảnh một cách độc lập, nên rất dễ xảy ra trường hợp một anchor được chọn làm positive sample cho tới 2 objects. Vì vậy, Global View là thực hiện gán positive samples cho anchors một cách có tương tác giữa các anchors với nhau, khiến việc chọn 1 anchor làm positive sample cho cả 2 objects là không xảy ra. DETR là nghiên cứu đầu tiên mà thực hiện LA theo dạng Global View. DETR thực hiện one-to-one assignment (OTO assigment - một object gán với một positive sample) bằng cách sử dụng thuật toán Hungarian. Nếu muốn tìm hiểu sâu hơn về LA trong DETR, các bạn có thể đọc bài giải thích của một kouhai trong team mình tại đây. Tuy nhiên, đấy là LA áp dụng cho Transformer, còn với CNN thì khác. Vì với tính chất của CNN là thu nhặt sự tương quan giữa các vùng lân cận với nhau, nên thay vì áp dụng OTO Assignment thì áp dụng one-to-many assignment (OTM Assignment - gán một object với một positive sample trọng điểm và các positive samples gần sample trọng điểm đó) sẽ tốt hơn với CNN. Và thuật toán Optimal Transport (OT) sẽ giúp giải quyết vấn đề nêu trên một cách tuyệt vời.

Bài toán Optimal Transport (OT)

Bài toán OT mô tả vấn đề như sau: Giả dụ có $m$ nguồn cung và $n$ nguồn cầu ở trong một khu vực. Nguồn cung thứ $i$ có $s_i$ đơn vị hàng hóa còn nguồn cầu thứ $j$ cần $d_j$ đơn vị hàng hóa. Chi phí vận chuyển mỗi đơn vị hàng hóa từ nguồn cung thứ $i$ sang nguồn cầu thứ $j$ kí hiệu là $c_{ij}$. Mục tiêu của OT là tìm một kế hoạch vận chuyển $\pi^* = \{\pi_{i,j}|i=1,2,...,m; j=1,2,...,n\}$ sao cho toàn bộ hàng hóa từ nguồn cung có thể chuyển sang nguồn cầu với chi phí nhỏ nhất:

$$\min_{\pi} \sum_{i=1}^{m} \sum_{j=1}^n c_{ij} \pi_{ij}$$

$$s.t. \sum_{i=1}^{m} \pi_{ij} = d_j, \quad \sum_{j=1}^{n} \pi_{ij} = s_i,$$

$$\sum_{i=1}^{m} s_i = \sum_{j=1}^{n} d_j,$$

$$\pi_{ij} \geq 0, \quad i=1,2,...,m; j=1,2,...,n$$

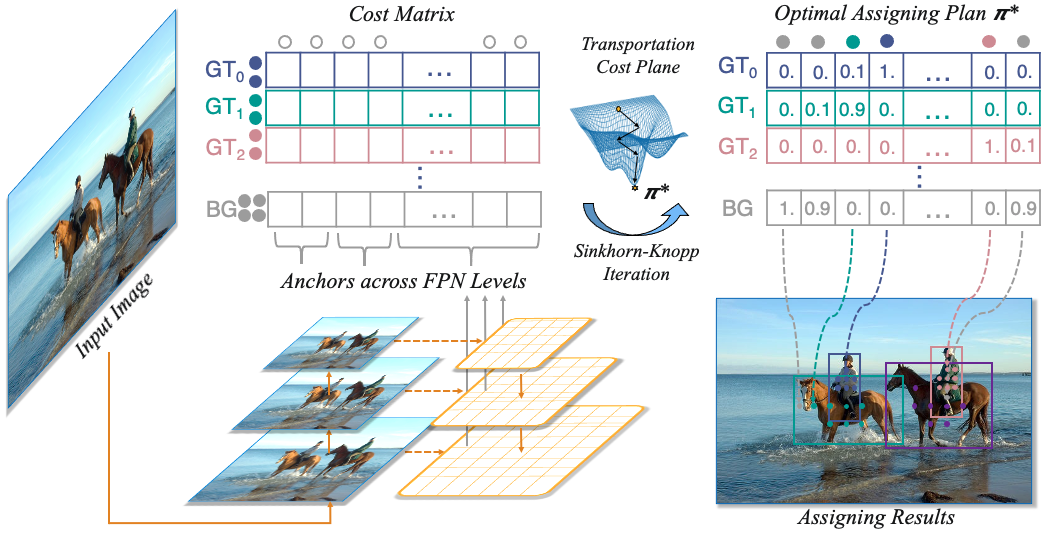
Áp dụng bài toán Optimal Transport (OT) cho LA

Oke áp dụng OT vào Label Assignment nào. Giả dụ, trong một ảnh $I$, ta có $m$ gt và $n$ anchors. Ta sẽ coi mỗi gt là một nguồn cung có thể cung cấp $k$ positive samples (hay nói cách khác là một gt sẽ cần phải được gán cho $k$ positive samples), tức là $s_i = k| i=1,2,...,m$, và mỗi anchor sẽ là một nguồn cầu cần một sample (anchor đó cần được gán là positive hoặc negative), tức là $d_j = 1| j=1,2,...n$. Chi phí vận chuyển một positive sample từ $gt_i$ sang anchor $a_j$, $c^{fg}$, được định nghĩa là phép cộng có hệ số của cls và reg loss:

$$c_{ij}^{fg} = L_{cls} (P_j^{cls} (\theta), G_i^{cls}) + \alpha L_{reg} (P_j^{box}(\theta), G_i^{box})$$

với $\theta$ là các parameters của model. $P_j^{cls}$ và $P_j^{box}$ là prediction của model về Classification score và Bounding Box của anchor $a_j$. $G_i^{cls}$ và $G_i^{box}$ là gt của Classification và Bounding Box của $gt_i$. $L_{cls}$ và $L_{reg}$ là Loss của Classification và Regression (Bounding Box). $\alpha$ là hệ số cân bằng.

Ngoài việc tìm và gán positive samples cho anchors, thì ta cũng cần phải chú ý tới negative samples, chiếm phần lớn trong mọi bức ảnh. Và để giải thuật toán OT thì ta cũng cần phải xét toàn bộ anchors trên một ảnh, nên ta sẽ thêm vào một nguồn cung nữa đó là Background (BG), nguồn cung này sẽ chỉ cung cấp negative samples. Số lượng negatives samples mà nguồn cung BG có thể cung cấp được là $n-m \times k$. Lúc này, chi phí để vận chuyển một đơn vị negative sample từ nguồn cung $bg$ sang anchor $a_j$ là:

$$c_j^{bg} = L_{cls} (P_j^{cls} (\theta), \oslash)$$

với $\oslash$ là class BG. Concat ma trận $c^{bg} \in \R ^{1 \times n}$ vào hàng cuối cùng của ma trận $c^{fg} \in \R^{m \times n}$, ta sẽ được ma trận chi phí vận chuyển bản full là $c \in \R ^{(m+1) \times n}$.
Với sự xuất hiện của nguồn cung BG, vector nguồn hàng có thể cung cấp $s$ như sau:

$$s_i = \begin{cases} k & \text{nếu} & i \leq m\\ n-m \times k & \text{nếu} & i=m+1 \\ \end{cases}$$

Oke dừng lại một chút để giải thích kĩ hơn về ma trận chi phí vận chuyển bản full (mình sẽ gọi tắt là cost matrix) này nào. Cost matrix được tạo từ 2 ma trận con: ma trận chi phí vận chuyển của positive samples và ma trận chi phí vận chuyển của negative samples. Cost matrix có số hàng là $(m+1)$ với $m$ là số object có trong ảnh, cũng là số hàng của $c^{fg}$, $+1$ là do thêm 1 hàng nữa từ ma trận $c^{bg}$; số cột của cost matrix là $n$, ứng với toàn bộ $n$ anchors trong ảnh đó. Các bạn nên vừa nhìn hình 4 vừa đọc thì sẽ dễ hiểu hơn.
Bài toán OT được giải sử dụng một thuật toán nữa gọi là Sinkhorn-Knopp Iteration. Mình xin phép không đi sâu vào thuật toán Sinkhorn-Knopp này vì nó không cần thiết để hiểu OTA. Sau khi giải xong, ta sẽ thu được kế hoạch vận chuyển tối ưu $\pi^*$, từ đó gán anchors với nguồn cung positive/negative samples tương ứng (Hình 4).

OTA viết theo dạng mã giả như sau:
Input:

• $I$ là một ảnh đầu vào
• $A$ là tập hợp các anchors trong ảnh
• $G$ là gt cho object trong ảnh $I$
• $\gamma$ và $T$: tham số gì đó liên quan đến thuật toán Sinkhorn-Knopp
• $\alpha$: hệ số cân bằng

Output: $\pi^*$: kế hoạch vận chuyển tối ưu

• $m \leftarrow |G|, n \leftarrow |A|$: $m$ là số lượng gt trong một ảnh, $n$ là số lượng anchors trong một ảnh
• $P^{cls}, P^{box} \leftarrow Forward(I, A)$: thực hiện forward pass một ảnh qua model
• $s_i(i=1,2,...,m) \leftarrow$ Dynamic $k$ estimation: thực hiện Dynamic $k$ estimation để tìm ra số lượng positive samples mà từng nguồn cung có thể cung cấp là bao nhiêu (sẽ nói cụ thể về Dynamic $k$ estimation sau). Chính là $s_i=k$ ở hệ phương trình trên kìa
• $s_{m+1} \leftarrow n - \sum_{i=1}^m s_i$: số negative samples mà nguồn cung BG có thể cung cấp
• $d_j(j=1,2,...,n) \leftarrow$ OnesInit: mỗi nguồn cầu anchor $j$ cần được gán là 1 sample, positive hoặc negative
• $c_{cls}^{ij} = L_{cls}(P_j^{cls}, G_i^{cls})$: tính Classification Loss của từng nguồn cung và nguồn cầu
• $c_{reg}^{ij} = L_{reg}(P_j^{box}, G_i^{box})$: tính Regression Loss của từng nguồn cung và nguồn cầu
• $c_{cp}^{ij} \leftarrow (A_j, G_i^{box})$: tính center prior cost (sẽ nói sau) của từng nguồn cung và nguồn cầu
• $fg$ cost: $c^{fg} = c_{cls} + \alpha c_{reg} + c_{cp}$
• $bg$ cost: $c^{bg} = L_{cls} (P_j^{cls} (\theta), \oslash)$
• concat ma trận $c^{bg}$ vào $c^{fg}$ để tạo ra cost matrix
• thực hiện Sinkhorn-Knopp Iteration thu được kế hoạch vận chuyển tối ưu $\pi^*$
• return $\pi^*$

Dynamic k estimation và Center Prior

Oke với OT cho LA, ta đã giải quyết được vấn đề (1) và (3) đã nêu phía trên. Còn vấn đề (2): Số lượng positive samples cho từng object là khác nhau; sẽ được giải quyết với Dynamic k estimation.
Với mỗi một object trong ảnh, OTA sẽ chọn ra top $q$ các predictions dựa trên giá trị IoU của Bounding Box dự đoán và gt Bounding Box. Sau khi có được $q$ giá trị IoU lớn nhất, với mỗi giá trị IoU nằm trong khoảng [0,1], ta sẽ cộng toàn bộ $q$ giá trị IoU đó lại rồi lấy phần nguyên, đó chính là số $k$ positive samples được chọn ra cho một object.
Center Prior là một sự cải tiến thêm do mọi người đều nhìn thấy rằng nếu gán positive samples cho các anchors có vị trí gần tâm của object thì sẽ khá là có lợi. Vì vậy, tác giả tạo ra một hình vuông có diện tích $r^2$ bao quanh tâm của object trên mỗi level của FPN. Vì vậy, muốn gán cho một anchor nào đó là positive sample, nó phải thỏa mãn 2 yếu tố: nằm trong Bounding Box của object và nằm trong hình vuông bao quanh tâm object.
Để hình dung được OTA hoạt động như nào thì mình đã có viết 1 đoạn code để hiển thị các thành phần quan trọng của OTA lên ảnh, kết quả ở hình 5.

SimOTA

Vì OTA yêu cầu phải giải quyết bài toán OT thông qua thuật toán Sinkhorn-Knopp Iteration, làm tăng thời gian training lên tới 20%, nên YOLOX đã thay thế OTA thành simOTA (simple OTA chứ k phải simp đâu nhé). Lúc này, simOTA chỉ quan tâm đến chi phí vận chuyển positive samples từ gt sang anchors, nên cost matrix sẽ chỉ còn lại như sau:

$$c_{ij} = L_{ij}^{cls} + \alpha L_{ij}^{reg}$$

đây chính là $c_{ij}^{fg}$ của OTA. simOTA lần này sẽ chỉ thực hiện Dynamic $k$ estimation và gán các top-k anchors ($k$ được chọn thông qua Dynamic $k$ estimation) thỏa mãn $c_{ij}$ thấp nhất làm positive samples luôn.

Kết

Phía trên là một bài phân tích tuy chưa đầy đủ nhưng cũng khá dài về Label Assignment, cũng như là simOTA, Label Assignment được sử dụng trong YOLOv7. Hy vọng trong phần sau của series phân tích YOLOv7 mình sẽ không cần phải nói quá kĩ về 1 phần nào đó như này nữa (vì không có gì khó, mới và ít bài phân tích như Label Assignment). Nếu có gì sai sót, mong các bạn có thể góp ý cho mình ở dưới comment.
Phần 3 của chuỗi YOLOv7 đã có ở đây: https://viblo.asia/p/paper-explain-yolov7-su-dung-cac-trainable-bag-of-freebies-dua-yolo-len-mot-tam-cao-moi-phan-3-018J253M4YK

Reference

YOLOv7: https://arxiv.org/abs/2207.02696