PageRank của Google

Trong những năm qua, Google đã trở thành công cụ tìm kiếm được sử dụng nhiều nhất trên toàn thế giới. Để trở thành điều đó, ngoài hiệu suất tìm kiếm cao và dễ sử dụng thì chất lượng kết quả tìm kiếm của Google cũng cao hơn so với các công cụ tìm kiếm khác. Chất lượng kết quả tìm kiếm này dựa trên PageRank, một phương pháp hữu hiệu để xếp hạng các trang web. Mục đích của bài viets này là cung cấp cho các bạn cách làm việc cũng như thuật toán được sử dụng trong PageRank. Trong nhiều năm qua, mặc dù thuật toán trong này được Google cải tiến nhiều lần để chất lượng tốt hơn, nhưng về bản chất thì cách hoạt động của PageRank là hầu như vẫn không thay đổi.

Khái niệm PageRank

Kể từ khi xuất hiện mạng internet, đã có rất nhiều cách lưu trữ và tổ chức các trang web nhằm mục đích dễ dàng cho việc tìm kiếm. Quay về lịch sử 1 chút thì ta có thể thấy yahoo lưu trữ các trang web trong các thư mục. Người ta gọi cách tổ chức này là web directories. Có một số thư mục như education, art, health,... Người dùng muốn tìm kiếm các trang web thì có thể vào các thư mục đó để tìm kiếm.

Ngày nay, người ta tổ chức, lưu trữ các trang web theo kiểu Web Search và tìm kiếm các trang web theo các từ khóa (search phrase). Sự xuất hiện của các search phrase trong các trang web chính là một trong những yếu tố chính để xếp hạng các trang web trong các công cụ tìm kiếm.

Nhưng để cho kết quả tìm kiếm được tốt hơn và đặc biệt là loại bỏ sự xuất hiện của các trang web spam dựa trên rank của các trang web, khái niệm về link popularity ra đời. Theo khái niệm này thì số trang liên kết tới một trang web sẽ đo độ quan trọng của trang web đó. Do đó một trang web được coi là quan trọng hơn nếu có nhiều trang web liên kết tới nó.

Ví dụ

www.stanford.edu có 23,400 trang web liên kết tới

www.joe-schmoe.com có 1 trang web liên kết tới

Rõ ràng là www.stanford.edu sẽ có rank cao hơn.

Trái ngược với khái niệm link popularity, PageRank không chỉ dựa trên tổng số trang liên kết với trang web mà nó còn dựa trên rank của các trang liên kêt tới nó. Rank của các trang liên kết lại dựa trên rank của các trang khác liên kết tới nó, Do đó, PageRank của một trang web luôn được xác định đệ quy bởi PageRank của các trang web khác.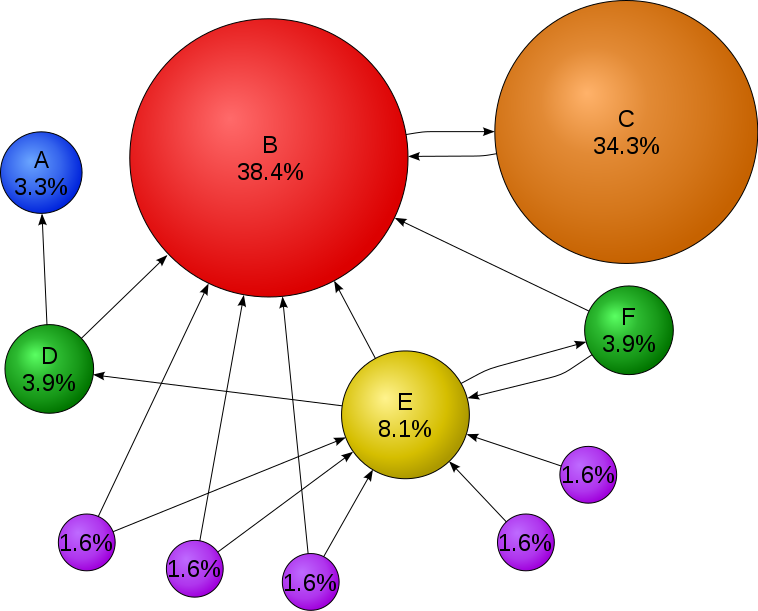

Trong ví dụ trên, ta có 11 trang web. Trang web B có nhiều trang web liên kết với nó nhất, do đó rank của trang web B đương nhiên là sẽ cao nhất. Trang web C mặc dù số trang web liên kết với nó ít hơn trang E nhưng mà nó được trang B liên kết tới, do đó nó sẽ có rank cao hơn trang E. Như vậy kết quả rank cuối cùng của một trang web dựa trên cáu trúc liên kết của toàn bộ các trang web. Cách tiếp cận này nghe mặc dù rất rộng và phức tạp, nhưng Page và Brin đã có thể đưa nó vào thực tế bằng một thuật toán tương đối tầm thường.

Thuật toán

Các trang web được biểu diễn bởi đồ thị có hướng (gọi là web graph) trong đó các đỉnh là các trang web, cạnh từ đỉnh j đến đỉnh i nếu trang web j liên kết tới trang web i.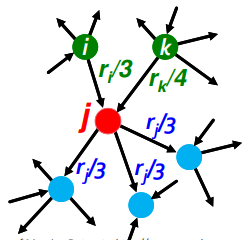

Gọi $ r_{i} $ là rank của page j, $d_{i}$ là bán bậc ra của node i (tức là số cạnh đi ra từ node ). Khi đó rank của trang j được tính theo công thức:

$$r_{j}=\sum_{i\rightarrow j} \frac{r_{i}}{d_{i}} (1)$$

Ví dụ chúng ta có web graph gồm 3 đỉnh a, y, m như hình vẽ

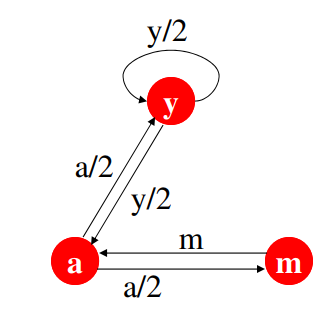
y có bán bậc ra là 2, a có bán bậc ra là 2, m có bán bậc ra là 1. a được trang y và trang m liên kết tới. Do đó:

$$r_{a} = \frac{r_{y}}{2}+r_{m}$$

Tương tự ta có

$$\left\{\begin{matrix} r_{y} = \frac{r_{y}}{2}+\frac{r_{a}}{2}\\ r_{m} = \frac{r_{a}}{2} \end{matrix}\right.$$

Ngoài ra ta có

$$r_{a}+r_{y}+r_{m} = 1$$

Giải hệ phương trình trên ta được

$$r_{y} = \frac{2}{5}$$

$$r_{a} = \frac{2}{5}$$

$$r_{m} = \frac{1}{5}$$

Đó là đối với web graph chỉ có 3 đỉnh. Trong thực tế, số đỉnh của web graph không chỉ có 3 đỉnh mà số lượng đỉnh hơn gấp nhiều lần, dẫn tới số biến của hệ phương trình cũng tăng. Vậy giải hệ phương trình đấy như thế nào? Chúng ta giải quyết vấn đề này bằng cách sử dụng cách tính xấp xỉ nghiệm của hệ phương trình này sau 1 số hữu hạn vòng lặp

Để hiểu về cách tính xấp xỉ này, trước hết chúng ta phải đưa hệ phương trình $(1)$ về dạng ma trận. Như chúng ta đã biết, mọi hệ phương trình đề có thể đưa về dạng $Ax = B$ trong đó $A,B$ là các ma trận hệ số. Như vậy hệ phương trình $(1)$ cũng hoàn toàn có thể đưa về dạng ma trận. Gọi ma trận $M$ trong đó phần tử $M_{ji} = \frac{1}{d_{i}}$ nếu node $i$ liên kết tới node $j$, $M_{ji} = 0$ nếu ngược lại, vector $r$ là vector cột có phần tử $r_{i}$ là rank của node $i$. Khi đó hệ phương trình $(1)$ có thể viết lại dưới dạng

$$Mr=r$$

Như vậy vector $r$ được gọi là vector riêng của ma trận $M$ (khái niệm vecto riêng bạn đọc có thể xem tại đây Sau đó chúng ta sử dụng thuật toán tính xấp xỉ để tính giá trị các phần tử của vector $r$. Giả sử có N trang web. Ban đầu khởi tạo các giá trị $r_{i} = \frac{1}{N}$. Sau đó sử dụng vòng lặp để cập nhật giá trị các phần tử $r_{i}$ trong vector $r$. $r^{(t)}$ là giá trị của vector $r$ tại vòng lặp thứ $t$. Lặp cho đến khi $l_{1} norm$ của $|r^{(t+1)}-r^{(t)}|$ nhỏ hơn hằng số $\varepsilon$ cho trước. ($norm$ của vector các bạn có thể xem tại đây. Dưới đây là thuật toán.

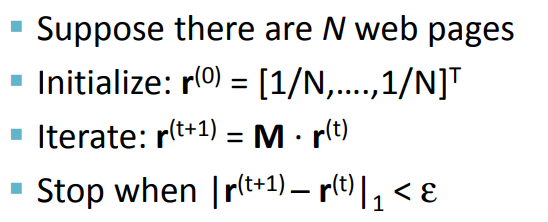
Ví dụ như trong trường hợp web graph có 3 node như ở trên, thì ma trận $M$ có dạng:

$$\begin{matrix} & y & a & m \\ y & 1/2 &1/2 & 0\\ a & 1/2 & 0 & 1\\ m & 0 & 1/2 & 0 \end{matrix}$$

vector $r$ có dạng:

$$\begin{matrix} r_{y}\\ r_{a}\\ r_m \end{matrix}$$

Khi đó ta có hệ phương trình

$$\begin{pmatrix} 1/2 &1/2 & 0\\ 1/2 & 0 & 1\\ 0 & 1/2 & 0 \end{pmatrix}\begin{pmatrix} r_{y}\\ r_{a}\\ r_m \end{pmatrix} = \begin{pmatrix} r_{y}\\ r_{a}\\ r_m \end{pmatrix}$$

Ban đầu ta khởi tạo $r_{y}=r_{a}=r_{m}=1/3$. Kết quả sau mỗi vòng lặp được cập nhật trong bảng sau:

$$\begin{pmatrix} r_{y}\\ r_{a}\\ r_m \end{pmatrix} = \begin{pmatrix} 1/3 &1/3 &5/12 &9/24 & &6/15 \\ 1/3& 3/6 & 1/3 & 11/24 &... & 6/15\\ 1/3& 1/3 & 3/12 & 1/6 & & 3/15 \end{pmatrix}$$

Như vậy kết quả cũng giống như khi ta giải hệ bằng phương pháp Gauss.

Thảo luận

Trên đây là cách cơ bản để đánh giá mức độ quan trọng của một trang web bằng phương pháp PageRank. Tuy nhiên, cách đánh giá trên còn 1 số bất cập ví dụ như khi ta loại bỏ 1 cạnh nối từ node m sang node a như thì web graph có dạng như hình vẽ

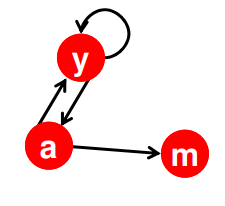
Trong trường hợp này, bán bậc ra tại đỉnh m $d_{m} = 0$. Trường hợp này, node m được gọi là node cụt. Lúc này ta không thể thay $d_{m}$ vào hệ phương trình $(1)$. Ta phải có một chút biến đổi, tôi sẽ đề cập trong những bài tiếp theo.

Tham khảo

http://www.mmds.org/mmds/v2.1/ch05-linkanalysis1.pdf

https://en.wikipedia.org/wiki/PageRank