Các thuật toán cơ bản trong AI - Phân biệt Best First Search và Uniform Cost Search (UCS)
Bài đăng này đã không được cập nhật trong 6 năm
Nếu bạn từng đọc các thuật toán trong AI (Artificial Intelligence - Trí tuệ nhân tạo), rất có thể bạn từng nghe qua về các thuật toán tìm kiếm cơ bản: UCS (thuộc chiến lược tìm kiếm mù) và Best First Search (thuộc chiến lược tìm kiếm kinh nghiệm). Khác nhau rõ từ khâu phân loại rồi, thế nhưng hai thuật toán này lại khiến không ít người cảm thấy bối rối khi lần đầu tìm hiểu, đơn giản vì nhìn về "tinh thần chung" hai thuật toán này khá giống nhau, ví dụ: "cả hai đều đánh giá chi phí và lựa chọn node tiếp theo với mục tiêu chi phí đường đi là thấp nhất". Vậy bài viết này chúng ta cùng tìm hiểu kỹ hơn để phân biệt hai thuật toán này nhé! 
Để hiểu về UCS và Best First Search, trước tiên chúng ta nên ôn tập qua hai khái niệm tìm kiếm mù và tìm kiếm kinh nghiệm.
Tìm kiếm mù
Chiến lược tìm kiếm mù là kỹ thuật tìm kiếm mà trong đó chúng ta không có hiểu biết gì về các đối tượng để có hướng dẫn tìm kiếm mà chỉ đơn thuần xem xét các đối tượng theo một hệ thống nào đó để phát hiện ra đối tượng cần tìm.
Tìm kiếm kinh nghiệm
Chiến lược tìm kiếm kinh nghiệm (tìm kiếm heuristic) là kỹ thuật tìm kiếm dựa vào kinh nghiệm và sự hiểu biết của chúng ta về vấn đề cần giải quyết để xây dựng nên hàm đánh giá hướng dẫn sự tìm kiếm.
Tiếp theo, cùng xem lại hai thuật toán gây mông lung nào!!
Thuật toán UCS
Thuật toán UCS là một thuật toán duyệt, tìm kiếm trên một cấu trúc cây, hoặc đồ thị có trọng số (chi phí). Việc tìm kiếm bắt đầu tại nút gốc và tiếp tục bằng cách duyệt các nút tiếp theo với trọng số hay chi phí thấp nhất tính từ nút gốc.
Mã giả:
begin
procedure UniformCostSearch(Graph, root, goal)
node:= root, cost = 0
frontier:= priority queue containing node only
explored:= empty set
do
if frontier is empty
return failure
node:= frontier.pop()
if node is goal
return solution
explored.add(node)
for each of node's neighbors n
if n is not in explored
if n is not in frontier
frontier.add(n)
else if n is in frontier with higher cost
replace existing node with n
Ví dụ cách hoạt động:
Hình 1. Đồ thị ví dụ cách hoạt động UCS
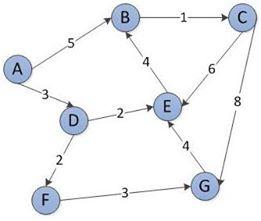
Cho đồ thị như hình trên, nút gốc là A, duyệt và tìm đường đi đến G với chi phí thấp nhất. Bảng dưới đấy mô tả các bước duyệt đồ thị Hình 1:
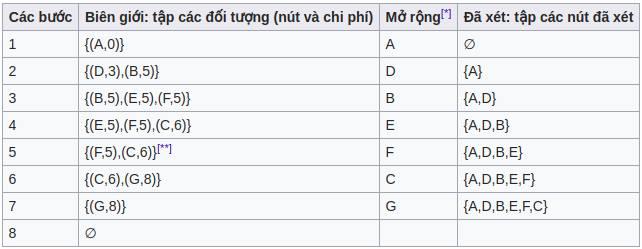
Trong đó:
[*] Nút được chọn để duyệt cho bước tiếp theo.
[**] B không được thêm vào hàng đợi vì nó đã nằm trong tập đã xét.
Thuật toán Best First Search
Trong tìm kiếm kinh nghiệm, chúng ta dùng hàm đánh giá để hướng dẫn tìm kiếm. Tìm kiếm tốt nhất - đầu tiên (Best First Search) là tìm kiếm theo bề rộng (Breadth First Search) được hướng dẫn bởi hàm đánh giá. Tư tưởng của thuật toán này là việc tìm kiếm bắt đầu tại nút gốc và tiếp tục bằng cách duyệt các nút tiếp theo có giá trị của hàm đánh giá là thấp nhất so với các nút còn lại nằm trong hàng đợi.
Mã giả:
procedure Best_First_Search;
begin
Khởi tạo danh sách L chỉ chứa trạng thái ban đầu;
loop do
if L rỗng then
{thông báo thất bại; stop};
Loại trạng thái u ở đầu danh sách L;
if u là trạng thái kết thúc then
{thông báo thành công; stop};
for mỗi trạng thái v kề u do
Xen v vào danh sách L sao cho L được sắp theo thứ tự tăng dần
của hàm đánh giá;
end;
Ví dụ cách hoạt động:
Hình 2. Đồ thị ví dụ cách hoạt động Best First Search
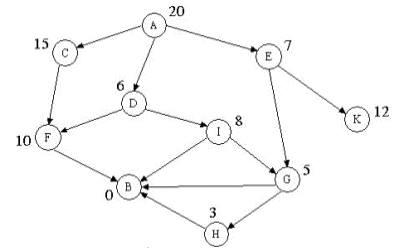
Cho đồ thị như hình trên, nút gốc là A, duyệt và tìm đường đi tốt nhất đến B. Cây dưới đây mô tả các bước duyệt đồ thị Hình 2:
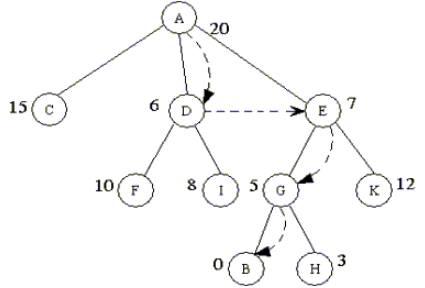
Đầu tiên phát triển đỉnh A sinh ra các đỉnh kề là C, D và E. Trong ba đỉnh này, đỉnh D có giá trị hàm đánh giá nhỏ nhất, nó được chọn để phát triển và sinh ra F, I. Trong số các đỉnh chưa được phát triển C, E, F, I thì đỉnh E có giá trị đánh giá nhỏ nhất, nó được chọn để phát triển và sinh ra các đỉnh G, K. Trong số các đỉnh chưa được phát triển thì G tốt nhất, phát triển G sinh ra B, H. Đến đây ta đã đạt tới trạng thái kết thúc.
Trong thủ tục này, chúng ta sử dụng danh sách L để lưu các trạng thái chờ phát triển, danh sách được sắp theo thứ tự tăng dần của hàm đánh giá sao cho trạng thái có giá trị hàm đánh giá nhỏ nhất ở đầu danh sách.
So sánh hai thuật toán
Ta có thể thấy cả hai thuật toán UCS và Best First Search đều sử dụng hàng đợi ưu tiên để lưu danh sách các node chờ duyệt, và đây có lẽ là nguyên nhân mấu chốt dẫn đến việc gây nhầm lẫn giữa hai thuật toán. Qua mỗi bước duyệt, các node còn lại trong danh sách đều được so sánh để sắp xếp lại và chọn ra node "được cho là" có chi phí thấp nhất. Nhưng sự khác nhau ở hai thuật toán có vẻ cũng nằm ở đây. Trước khi sắp xếp lại danh sách các node, UCS vì không có hàm đánh giá nên nó cần tự thân vận động:
Chi phí node N = Chi phí từ gốc đến node ngay trước N + Chi phí từ node ngay trước N đến N
Trong khi Best First Search thì không phải làm gì cả, vì nó đã có hàm đánh giá ngay tại node rồi. Bên cạnh đó, chúng ta cũng nhận thấy rằng Best First Search nồng nặc mùi greedy (chiến lược tham ăn) .
Dưới đây là một số so sánh giữa hai thuật toán:
| Tiêu chí đánh giá | UCS | Best First Search |
|---|---|---|
| Chiến lược | Tìm kiếm mù, không sử dụng hàm đánh giá | Tìm kiếm kinh nghiệm, sử dụng hàm đánh giá |
| Chi phí | Tính từ node bắt đầu đến node hiện tại | Tính từ node trước đến node hiện tại |
| Độ phức tạp theo thời gian | O(b^d) | O(b^m) |
| Độ phức tạp theo không gian | O(b^d) | O(b^m) |
| Danh sách các node chờ duyệt | Hàng đợi ưu tiên | Hàng đợi ưu tiên |
| Khả năng tìm nghiệm | Luôn tìm thấy | Quá trình tìm kiếm có thể đi xa khỏi lời giải. Kỹ thuật này chỉ xét một phần của không gian và coi đó là phần hứa hẹn hơn cả. Có thể bị kẹt trong vòng lặp. |
| Tối ưu | Có nếu cost > 0 | Không |
| Ghi chú | Khi đồ thi có chi phí ở mỗi bước là như nhau thì thuật toán trở thành phương pháp tìm kiếm theo chiều rộng. | Một hàm đánh giá tốt có thể giảm thời gian và không gian nhớ một cách đáng kể. |
Với d, m là độ sâu của cây cần duyệt và mỗi trạng thái khi được phát triển sẽ sinh ra b trạng thái kề (b được gọi là nhân tố nhánh).
Bài viết hơi dài, hẹn gặp lại các bạn trong một bài viết khác  Nếu có câu hỏi thắc mắc, hay ý kiến thảo luận, đóng góp các bạn bình luận dưới bài viết này nhé!!
Nếu có câu hỏi thắc mắc, hay ý kiến thảo luận, đóng góp các bạn bình luận dưới bài viết này nhé!! 
All rights reserved