1. Overview (Tổng Quan)

Là một lập trình viên hẳn các bạn ai cũng đã từng phải sử dụng thuật toán sắp xếp. Trong SERI về thuật toán tìm kiếm này chúng ta sẽ tìm hiểu tư tưởng của các loại thuật toán sắp xếp cơ bản nhất: Bubble Sort, Insertion Sort, Merge Sort, Heap Sort, QuickSort, Radix Sort, Counting Sort, Bucket Sort, ShellSort. Trong bài viết này mình chúng ta sẽ tìm hiểu về Selection Sort :

• Thuật toán Selection Sort là gì?
• Các thành phần chính của thuật toán Selection Sort.
• Cách triển khai thuật toán Selection Sort qua ví dụ.

Toàn bộ ví dụ mình sẽ sử dụng python giúp các bạn dễ hiểu và dễ nắm bắt. Let's do it ^^

2. Selection Sort (Sắp Xếp Chọn)

Thuật toán Selection Sort sắp xếp một mảng bằng cách liên tục tìm phần tử nhỏ nhất (xét theo thứ tự tăng dần) từ phần chưa được sắp xếp và đặt nó ở đầu. Thuật toán duy trì hai mảng con trong một mảng nhất định.

1. Mảng con đã được sắp xếp.

2. Mảng con còn lại chưa được sắp xếp.

Trong mỗi lần lặp lại sắp xếp lựa chọn, phần tử tối thiểu (xét theo thứ tự tăng dần) từ mảng con chưa được sắp xếp sẽ được chọn và chuyển đến mảng con đã sắp xếp.

Ví dụ sau giải thích các bước trên:

//Dãy chưa sắp xếp
arr[] = 64 25 12 22 11

// Tìm phần tử bé nhất trong dãy arr[0...4]
// đưa phần tử đó lên đầu dãy arr[0...4]
**11** 25 12 22 64

// Tìm phần tử bé nhất trong dãy arr[1...4]
// đưa phần tử đó lên đầu dãy arr[1...4]
11 **12** 25 22 64

// Tìm phần tử bé nhất trong dãy arr[2...4]
// đưa phần tử đó lên đầu dãy arr[2...4]
11 12 **22** 25 64

// Tìm phần tử bé nhất trong dãy arr[3...4]
// đưa phần tử đó lên đầu dãy arr[3...4]
11 12 22 **25** 64 

Dưới đây là sơ đồ khối theo từng bước thực hiện của thuật toán trên

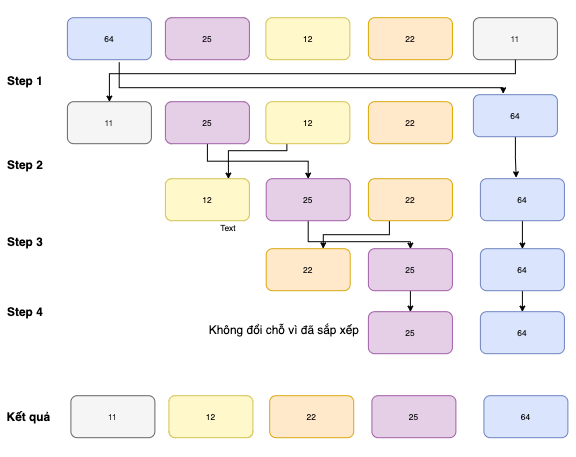
Dưới đây là cách cài đặt thuật toán bằng ngôn ngữ Python:

import sys

A = [64, 25, 12, 22, 11]
  
for i in range(len(A)):
      
    # Tìm kiếm phần tử bé nhất trong dãy chưa được sắp xếp 
    min_idx = i
    for j in range(i+1, len(A)):
        if A[min_idx] > A[j]:
            min_idx = j
              
    # Đổi chỗ phần tử bé nhất với phần tử đầu tiên        
    A[i], A[min_idx] = A[min_idx], A[i]
  
# Test Kết Quả
print ("Sorted array")
for i in range(len(A)):
    print("%d" %A[i]), 

Đây là kết quả

Sorted array: 
11 12 22 25 64

Thuật toán Selection Sort là một thuật toán khá đơn giản khi cài đặt. Thuật toán này có độ phức tạp là O(n2) vì có 2 vòng lặp.

3. Conclusion (Kết Luận)

Trong bài viết này chúng ta đã tìm hiểu được thuật toán sắp xếp chọn (Selection Sort). Có cài nhìn tổng quan về thuật toán. Cách cài đặt thuật toán bằng ngôn ngữ Python. Độ thức tạp thuật toán. Rất mong đã đem lại cho bạn đọc những kiến thức thú vị. Nếu thấy hay bạn nhớ bấm follow mình nhé !!

Dưới đây là các bài viết cùng Seri :

• Thuật Toán Sắp Xếp Chèn (Insertion Sort): https://viblo.asia/p/thuat-toan-insertion-sort-don-gian-bWrZnVapZxw
• Thuật Toán Sắp Xếp Nổi Bọt ( Bubble Sort ): https://viblo.asia/p/thuat-toan-bubble-sort-don-gian-yMnKM8Oz57P