Hôm nay mình sẽ tìm hiểu về một thuật toán được áp dụng rất nhiều trong thực tế, đó là thuật toán chia để trị và một số ví dụ áp dụng trong thực tế để giúp hiểu sâu hơn về nó.

1. Khái niệm

• Chia để trị là 1 phương pháp áp dụng cho các bài toán có thể giải quyết bằng cách chia nhỏ ra thành các bài toán con từ việc giải quyết các bài toán con này. Sau đó lời giải của các bài toán nhỏ được tổng hợp lại thành lời giải cho bài toán ban đầu.
  

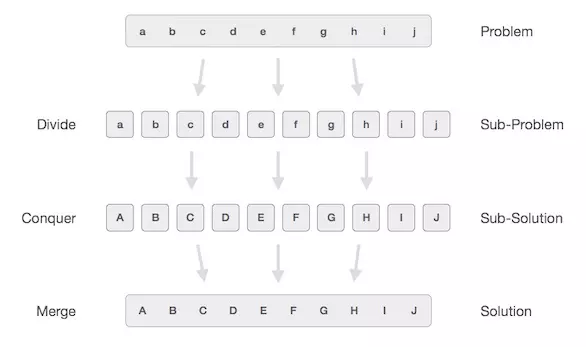
Các bài toán có thể giải quyết bằng phương pháp chia để trị thông qua 3 bước:

Bước 1: Chia/Tách nhỏ

Tại bước này thì bài toán ban đầu sẽ được chia thành các bài toán con cho đến khi không thể chia nhỏ được nữa. Các bài toán con kiểu sẽ trở thành 1 bước nhỏ trong việc giải quyết bài toán lớn.

Bước 2: Trị/Giải quyết bài toán con

Tại bước này ta sẽ phải tìm phương án để giải quyết cho bài toán con một cách cụ thể.

Bước 3: Kết hợp lời giải lại để suy ra lời giải

Khi đã giải quyết xong cái bài toán nhỏ, lặp lại các bước giải quyết đó và kết hợp lại những lời giải đó để suy ra kết quả cần tìm (có thể ở dạng đệ quy).
Nói lý thuyết không có vẻ sẽ không "thấm" hãy cùng đến với các ví dụ để hiểu rõ hơn về nó xem

2. Áp dụng

Mình sẽ trình bày 2 bài toán áp dụng trong thực tế của chia để trị đó là tìm kiếm nhị phân và thuật toán quick-sort.

2.1 Tìm kiếm nhị phân

Tìm kiếm nhị phân là một thuật toán dùng để tìm kiếm 1 phần tử trong một danh sách đã được sắp xếp. Thuật toán hoạt động như sau:
Bước 1(Chia): Danh sách ban đầu sẽ được chia thành 2 nửa
Bước 2 (Trị): Trong mỗi bước, so sánh phần tử cần tìm với phần tử nằm ở chính giữa danh sách. Nếu hai phần tử bằng nhau thì phép tìm kiếm thành công và thuật toán kết thúc. Nếu chúng không bằng nhau thì tùy vào phần tử nào lớn hơn, thuật toán lặp lại bước so sánh trên với nửa đầu hoặc nửa sau của danh sách. Vì số lượng phần tử trong danh sách cần xem xét giảm đi một nửa sau mỗi bước, nên thời gian thực thi của thuật toán là hàm lôgarit.
Bước 3: Bằng việc lặp lại cách giải quyết như bước 2 ta sẽ tìm được kết quả.

  int binarySearch(int array[], int left, int right, int x)
    { 
        // nếu chỉ số left > right dừng lại và return -1 không có kết quả
        if (left > right) return -1;
        // tìm chỉ số ở giữa của mảng
        int mid = (left + right) / 2;
        
        // nếu số cần tìm bằng số ở giữa của mảng thì return
        if (x == array[mid]) 
            return mid;
        
        // nếu số cần tìm nhỏ hơn số ở giữa của mảng thì tìm sang nửa bên trái
        if (x < array[mid]) 
            return binarySearch(array, left , mid-1, x);
  
        // nếu số cần tìm lớn hơn số ở giữa của mảng thì tìm sang nửa bên phải
        if (x > array[mid]) 
            return binarySearch(array, mid+1 , right, x);
    }

2.2 Quicksort

Thuật toán quicksort được áp dụng rất nhiều trong thực tế, hãy cùng tìm hiểu thuật toán này áp dụng chia để trị như thế nào.
Bước 1(chia): Thuật toán quicksort chia danh sách cần sắp xếp mảng array[1..n] thành hai danh sách con có kích thước tương đối bằng nhau nhờ chỉ số của phần tử gọi là chốt, ta có thể chọn chốt là phần tử ở giữa, ở cuối, ở đầu hoặc phần tử ngẫu nhiên nào trong mảng.
Bước 2(trị): Sau khi đã chia thành 2 mảng dựa vào phần tử chốt nhiệm vụ của bước này là phải sắp xếp sao cho: những phần tử nhỏ hơn hoặc bằng phần tử chốt được đưa về phía trước và nằm trong danh sách con thứ nhất, các phần tử lớn hơn chốt được đưa về phía sau và thuộc danh sách đứng sau(Trường hợp sắp xếp tăng dần). Cứ tiếp tục chia như vậy tới khi các danh sách con đều có độ dài bằng 1
Bước 3: Bằng việc lặp các bước giải quyết các bài toán con trên ta sẽ thu được kết quả là mảng sẽ được sắp xếp.
Dưới đây là hình ảnh minh họa việc thực hiện thuật toán quicksort:

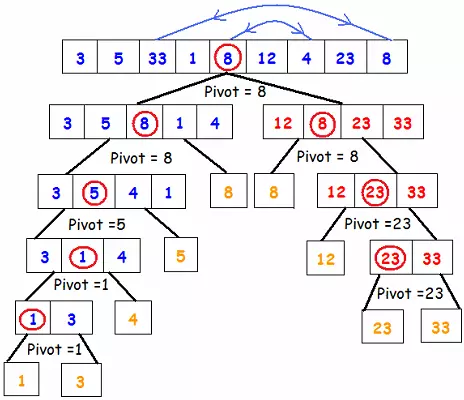
// hàm giải quyết việc sắp xếp các phần tử ở hai đầu của mảng 
// dựa vào phần tử chốt là phần tử cuối mảng
    int partition(int arr[], int low, int high) 
    { 
        // chốt được chọn ở đây là phần tử cuối mảng
        int pivot = arr[high];  
        int i = (low-1);  
        for (int j=low; j<high; j++) 
        {  
            // nếu phần tử nhỏ hơn hoặc bằng với chốt
            if (arr[j] <= pivot) 
            { 
                i++; 
  
                // đổi chỗ arr[i] và arr[j] 
                int temp = arr[i]; 
                arr[i] = arr[j]; 
                arr[j] = temp; 
            } 
        } 
        
        // đổi chỗ arr[i+1] và arr[high] (chốt)
        int temp = arr[i+1]; 
        arr[i+1] = arr[high]; 
        arr[high] = temp; 
        
        // trả về chỉ số của chốt
        return i+1; 
    } 
    
    // Hàm thực hiện quicksort
    void sort(int arr[], int low, int high) 
    { 
        // nếu chỉ số của đầu mảng nhỏ hơn chỉ số cuối mảng
        if (low < high) 
        { 
            // tìm chỉ số của chốt sau khi đã thực hiện sắp xếp
            int pi = partition(arr, low, high); 
  
            // lặp lại các bước với mảng từ phần tử đầu tiên đến chốt - 1
            // và từ chốt + 1 đến phần tử cuối cùng của mảng.
            sort(arr, low, pi-1); 
            sort(arr, pi+1, high); 
        } 
    } 

3. Kết luận

Như vậy chúng ta đã tìm hiểu được thuận toán chia để trị và việc áp dụng nó vào một số bài toán thực tế. Trong thực tế việc chia để trị cũng là cách để giải quyết khi ta gặp task khó, chia chúng thành các task nhỏ hơn để làm thay vì làm cả một task to, việc chia task nhỏ hơn sẽ giúp thực hiện dễ dàng hơn và có thể ít "ăn" comment hơn . Hi vọng bài viết sẽ giúp ích cho mọi người, nếu có gì thảo luận hay góp ý hãy comment xuống phía dưới nhé. Cảm ơn đã đọc! (seeyou)
References:
https://en.wikipedia.org/wiki/Divide_and_conquer_algorithm https://www.geeksforgeeks.org/divide-and-conquer-algorithm-introduction/