Tìm hiểu về các thuật toán Searching for Patterns (Naive Pattern Searching, KMP (Knuth Morris Pratt) Pattern Searching)

Bài đăng này đã không được cập nhật trong 6 năm

Ngẫm:

Mình thường lập trình với các ngôn ngữ cấp cao, nên các function tìm kiếm xuất hiện chuỗi con trong chuỗi cha khá phổ biến. Với PHP thì có strpos, javascript thì có indexOf. Vậy chúng dùng những thuật toán gì, sau đây mình cũng tìm hiểu.

1) Naive Pattern Searching

Rõ ràng ai đã từng họ tin học cấp ba với parcal đều đã từng trải qua bài toán tìm kiếm index chuỗi con. Và theo mình biết thì đây là cách phổ biến các bạn áp dụng, vì tính tường minh của nó

// C program for Naive Pattern Searching algorithm
#include <stdio.h>
#include <string.h>
 
void search(char* pat, char* txt)
{
    int M = strlen(pat);
    int N = strlen(txt);
 
    /* A loop to slide pat[] one by one */
    for (int i = 0; i <= N - M; i++) {
        int j;
 
        /* For current index i, check for pattern match */
        for (j = 0; j < M; j++)
            if (txt[i + j] != pat[j])
                break;
 
        if (j == M) // if pat[0...M-1] = txt[i, i+1, ...i+M-1]
            printf("Pattern found at index %d \n", i);
    }
}
 
/* Driver program to test above function */
int main()
{
    char txt[] = "AABAACAADAABAAABAA";
    char pat[] = "AABA";
    search(pat, txt);
    return 0;
}

Quá dễ hiểu phải không nhỉ, cơ bản là cứ loop qua mỗi phần từ, với mỗi phần tử này ta có 1 biến chạy khác để so sánh matching, nếu đúng thì ta xuất ra index bắt đầu maching, sai thì nâng lên ví trí bắt đầu ở ví trí tiếp theo và reset lại vòng lặp 2, và bắt đầu tiếp qúa trình trên.
Best case thì độ phức tạp là O(n), worst case thì độ phức tạp là O(m*(n-m+1)).

2) KMP (Knuth Morris Pratt) Pattern Searching

Cùng xét một trường hơp:

 text = "ABABABCABABABCABABABC"
 pattern =  "ABABAC" (not a worst case, but a bad case for Naive)

Rõ ràng đây là một trường hợp xấu của thuật toán 1, vì rõ ràng ngay vòng lặp đâù tiên bạn đã biết được ABABAB không match nhưng rồi bạn cũng phải check tiếp BABABC, ABABCA , để cải thiện điều trên, KMP đề xuất một mảng sub pattern để nếu gặp phải kết quả mismatch thì thay vì bắt đầu tìm kiếm lại từ đầu, chúng ta đã biết được text trong ô window tiếp theo để tránh việc matching kí tự mà ta biết nó đã match rồi (ở đây là ABABA).

Mình cũng tìm hiểu kĩ quả ví dụ:

Ví dụ:
txt = "AAAAABAAABA" 
pat = "AAAA"

txt = "AAAAABAAABA" 
pat = "AAAA"  
Lần đầu mình đã tìm được matching ngay vòng lặp đầu tiên.

Lần tiếp theo, khi so sánh 
txt = "AAAAABAAABA" 
pat =  "AAAA" [Pattern shifted one position]

Ở đây ta thấy rõ sự tối ưu của KMP, ngay tại kí tự thứ 2 của txt, 
Naive phải tiếp tục loop để maching 3 chữ AAA, còn KMP chỉ so sánh kí tự thứ 4 của pat, 
vì nó biết rõ 3 chữ AAA đầu đã match.

Để làm được điều trên, nó xây dựng một sub pattern để lưu một mảng độ dài maximum các prefix matching:

Ví dụ:
Cho pattern “AAAA”, 
lps[] is [0, 1, 2, 3]

Cho pattern “ABCDE”, 
lps[] is [0, 0, 0, 0, 0]

Cho pattern “AABAACAABAA”, 
lps[] is [0, 1, 0, 1, 2, 0, 1, 2, 3, 4, 5]

Cho pattern “AAACAAAAAC”, 
lps[] is [0, 1, 2, 0, 1, 2, 3, 3, 3, 4] 

Cho pattern “AAABAAA”, 
lps[] is [0, 1, 2, 0, 1, 2, 3]

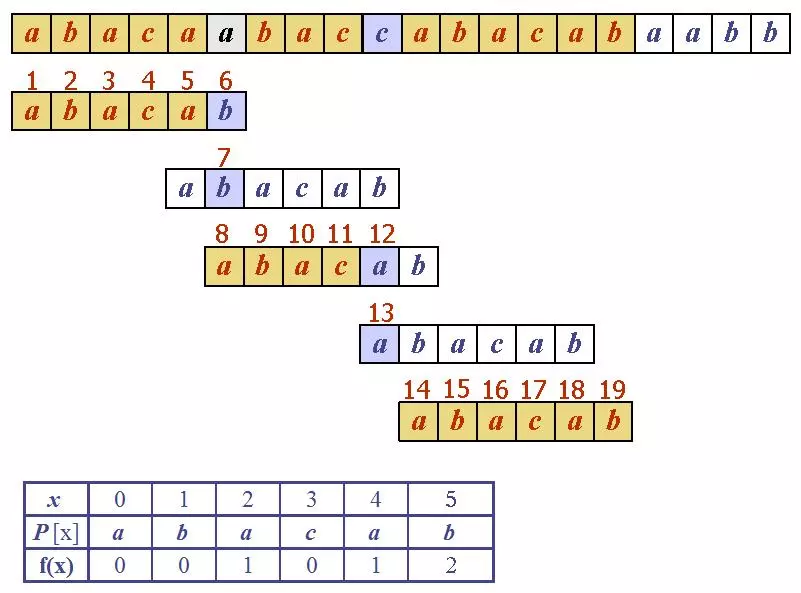
Triết lí quả là rất đơn giản, ngay khi so sánh thấy một phần tử không match, ta dịch chuyển khung pattern tới điểm có prefix matching dài nhất rồi bắt đầu từ đó so sánh tiếp, điều đó giúp độ phức tạp chỉ là O(n) (love)

Code:

def kmp(pattern, text):
    """
    The Knuth-Morris-Pratt Algorithm for finding a pattern within a piece of text
    with complexity O(n + m)
    1) Preprocess pattern to identify any suffixes that are identical to prefixes
        This tells us where to continue from if we get a mismatch between a character in our pattern
        and the text.
    2) Step through the text one character at a time and compare it to a character in the pattern
        updating our location within the pattern if necessary
    """

    # 1) Construct the failure array
    failure = get_failure_array(pattern)
    print('failure', failure)
    # 2) Step through text searching for pattern
    i, j = 0, 0  # index into text, pattern
    while i < len(text):
        if pattern[j] == text[i]:
            if j == (len(pattern) - 1):
                return True
            j += 1

        # if this is a prefix in our pattern
        # just go back far enough to continue
        elif j > 0:
            j = failure[j - 1]
            continue
        i += 1
    return False


def get_failure_array(pattern):
    """
    Calculates the new index we should go to if we fail a comparison
    :param pattern:
    :return:
    """
    failure = [0]
    i = 0
    j = 1
    while j < len(pattern):
        if pattern[i] == pattern[j]:
            i += 1
        elif i > 0:
            i = failure[i-1]
            continue
        j += 1
        failure.append(i)
    return failure



# Test 1)
pattern = "abc1abc1abc12"
text1 = "alskfjaldsabc1abc1abc12k23adsfabcabc"
text2 = "alskfjaldsk23adsfabcabc"
print(kmp(pattern, text1))
print(kmp(pattern, text2))

Output:

failure [0, 0, 0, 0, 1, 2, 3, 4, 5, 6, 7, 8, 0]
True
failure [0, 0, 0, 0, 1, 2, 3, 4, 5, 6, 7, 8, 0]
False

Worst case của KMP cũng chỉ là O(n), quá good phải không các bạn. Cảm ơn các bạn đã đọc.

Reference:

Algorithm

Ngẫm:

1) Naive Pattern Searching

2) KMP (Knuth Morris Pratt) Pattern Searching

Mục lục