Một vài ứng dụng của 0 và 1 có thể bạn chưa biết

Tổng hợp các chiêu thức combo cực mạnh trong thế giới phần mềm mà bạn có thể tạo ra chỉ từ 2 chữ số đơn giản nhất: 0 và 1.

First things first

Hê lô các bạn, mình - Minh Monmen - đã trở lại với các bạn chả trong sự kiện gì cả đây. Sau một thời gian rất dài mải mê chinh chiến (thất nghiệp - rải CV) và yêu đương (người tình kiếp trước 14 tháng tuổi) thì mình cũng tranh thủ được chút thời gian của một đêm không mưa gió để hoàn thành bài viết đã ấp ủ từ rất lâu này. Thế nhưng trước khi vục mặt vào đống chữ nghĩa lủng củng của một ông bô bỉm sữa thì hãy dành chút thời gian tán dóc về sự ra đời của bài viết này nhé.

Chắc hẳn anh chị em nào đang đọc bài viết này thì cũng đã từng nghe, từng học về hệ nhị phân (binary), về ngôn ngữ máy, về bit, byte, kilobyte, megabyte,... hết rồi. Mấy cái đấy toàn mấy cái thứ khô khan chán đời cả, thế nên mình cũng không rảnh hơi để mà nói sâu về mấy cái khái niệm ở trên làm gì nữa. Kiến thức thì bao la mà sự học là biển cả. Chỉ là nếu như đi ngồi học khái niệm, học kiến thức không thôi thì cảm giác nó cứ như nhai rơm nhai rạ vậy. Thế nên mình nghĩ chắc một chút mục đích thực tế hay ho sẽ là thứ khiến cho kiến thức sách vở trở nên thú vị hơn rất nhiều. Và đó là lý do chúng ta ngồi đây hôm nay.

Ô kê chưa? Let's start!

Bit là gì?

Nói thì bảo nó khô khan chán đời nhưng vẫn phải đảo qua nó một tí các bạn ạ, không thì đọc mấy cái sau như chó xem tát ao mất.

Bit - hay binary digit, là đơn vị nhỏ nhất dùng để biểu diễn thông tin trong máy tính. Nó chỉ có 2 giá trị là 1 và 0, biểu thị cho sự có và không, đóng và mở, bật và tắt,... Chỉ có 2 giá trị thôi nên đừng có cố văn thơ lai láng hay triết lý có có không không gì ở đây nhé.

Kiến thức này thì chắc là ai cũng biết cả rồi, cơ bản quá mà. Ok, next nào.

1 byte = 8 bit

Cái này ai cũng biết. 1 Byte có thể chứa 2^8 = 256 giá trị khác nhau và thường được dùng để chứa bảng ký tự Latin ASCII hay là độ dài của kiểu dữ liệu char trong các ngôn ngữ lập trình. Cái này cũng quá cơ bản rồi. Ok, next.

4 byte = 32 bit

Đây là kích thước của một số nguyên int thường dùng trong lập trình, có thể chứa 2^32 = 4,294,967,296 giá trị khác nhau. Thường biểu diễn số từ -2^31 đến 2^31 - 1, hoặc từ 0 đến 2^32 - 1. Cái này thường gặp. Ok, next.

8 byte = 64 bit

Ok cái này thì ít gặp hơn, đây là kiểu dữ liệu long, thường dùng để biểu diễn số nguyên lớn hơn, có thể chứa 2^64 giá trị khác nhau, tương đương với khoảng số từ 0 đến 18,446,744,073,709,551,615 (20 chữ số tất cả). Đây cũng chính là cái id facebook mà bạn vẫn hay gặp nè:

Ví dụ group Viblo Community:

https://www.facebook.com/1026180787845556

Một vài ứng dụng của bit

Vậy là từ bit ta sẽ ghép dần thành byte, rồi ghép nhiều byte lại ta có thể biểu diễn được các kiểu số và chữ khác nhau. Thì sao nhỉ? Có gì hay ho ở đây không?

Khoan hãy chán nản, giờ mới là thứ hay ho nè:

Posix file permission

Một ứng dụng của bit cực kỳ quen thuộc, đập vào mắt chúng ta hàng ngày nhưng ta lại ít để ý. Nếu bạn đã nghe tới 777, 755, 644,... thì đây chính là quyền truy cập file trong hệ điều hành Unix/Linux. Những con số này biểu diễn cho quyền của 3 loại user: owner, group, other tương ứng với 3 loại quyền là read, write, execute.

Hồi xưa mình thường tự hỏi? Tại sao chỉ từ con số 755, người ta có thể biết chính xác là owner có những quyền gì, group có những quyền gì, other có những quyền gì? Không lẽ chỉ từ việc con số 7 chỉ có thể là tổng của 4 + 2 + 1 và 5 thì là 4 + 1? Tại sao không phải là 3 + 2???

Cho tới khi mình học về bit, thì mình mới hiểu được rằng bản chất 3 con số này là 3 nhóm bit đặt cạnh nhau, mỗi nhóm gồm 3 bit, mỗi bit biểu diễn cho 1 quyền. 1 là có quyền mà 0 là không có quyền. Trong con mắt của máy tính, 5 tức là 1-0-1, nghĩa là có quyền 1-read, 0-write và 1-execute. Chứ không có tổng 4 với 1 hay 3 với 2 gì ở đây hết.

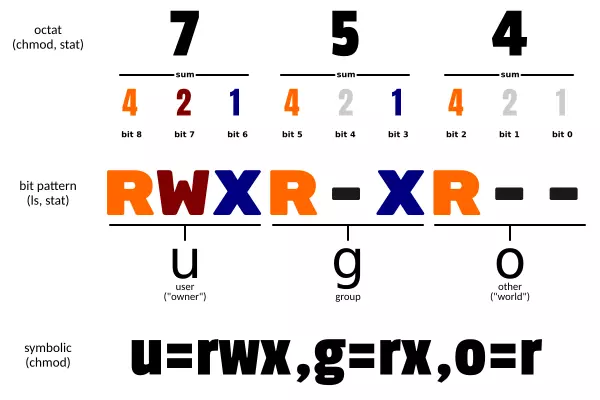
Vậy là chỉ với 9 bit (lớn hơn 1 byte 1 chút), người ta đã biểu diễn được tất cả 9 quyền truy cập của file cho các nhóm người dùng. Rất hiệu quả phải không?

Các loại Global ID

Bạn đã bao giờ tự hỏi: Nếu như ID facebook của bạn chỉ là 1 con số vô tri (như chúng ta vẫn thường đánh ID user trong DB bằng số tự tăng ấy) thì làm cách nào mà chỉ cần nhập địa chỉ https://facebook.com/<id> là facebook đã biết cái id này là của một người, một page, một group... luôn không? Không lẽ ID nào cũng phải đi tra cứu DB thử xem nó là cái gì à?

Không, mấy cái ID đó không vô tri như bạn nghĩ mà đều ẩn chứa rất nhiều thông tin bên trong cả. Nếu như bạn đã nghe đến cái tên: Snowflake ID, Sonyflake ID, Instagram ID,... thì facebook ID rất có thể cũng có cùng cơ chế với những loại trên.

Những kiểu ID này thường được biểu diễn bằng 1 số long với độ dài 64 bit, từ đó cho chúng ta rất nhiều sự kết hợp để có thể chứa đựng những thông tin khác nhau như thời gian sinh ID, loại ID, máy sinh ra ID, số thứ tự,... Ví dụ với Snowflake:

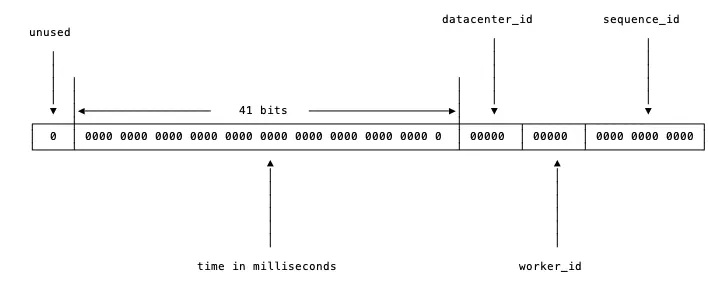
Hay như Sonyflake:

Instagram cũng sử dụng 1 biến thể của Snowflake ID với cách sắp xếp bit khác nhau:

Mình cũng đã từng tự chế ra Global ID với những thông tin về loại dữ liệu, ngày giờ tạo, random part,... theo ý tưởng của các loại ID trên khi còn làm mạng xã hội. Các bạn có thể dùng luôn thư viện có sẵn, hoặc tự chế (và tự xử lý các vấn đề của nó như mình)

So với những ID dài như Mongo ID (96 bits) hay UUID (128 bits - nhưng thường được lưu dạng string với 36 ký tự) thì việc sử dụng Snowflake ID, Sonyflake ID (64 bits),... tiết kiệm bộ nhớ hơn khá nhiều mà vẫn đảm bảo số lượng ID lớn, khó đoán, distributed,...

Cái này quan trọng nha, nhất là khi các bạn thiết kế Database và các ID này thường được đưa vào index (và index size phải được fit vào RAM). Một index với ID 64 bits nếu nặng 1GB thì sẽ có thể nặng tới 1,5 hoặc 2GB nếu dùng Mongo ID hay UUID (nếu được lưu đúng cách, còn lưu dạng string 36 ký tự thì còn nặng hơn vài lần nữa)

Bitset

Mình biết đến khái niệm bitset vào năm 2018, khi tham gia Vietnam Web Summit và nghe bài nói của bác Châu Nguyễn Nhật Thanh bên VNG chia sẻ về quá trình xây dựng ZingMe, ứng dụng mạng xã hội lớn nhất VN lúc bấy giờ. Phải nói đấy thực sự là một bài nói cho mình mở mang đầu óc, thay đổi hoàn toàn mindset của mình về việc xử lý dữ liệu lớn và cách tiếp cận với những bài toán ấy.

Vậy bitset là gì và tại sao nó lại thay đổi hẳn cả mindset của mình như thế?

Bitset (hay còn gọi là bitmap) đơn giản là 1 dãy bit. Nó là khởi nguồn của mọi loại dữ liệu.

Nghe khiếp không? Câu sau thật ra là mình chém vào cho kinh thôi. Nhưng về bản chất thì mọi thứ chúng ta lưu vô máy tính cuối cùng đều là những dãy bit, nên nói bitset là khởi nguồn của mọi loại dữ liệu cũng không ngoa lắm.

Bài nói của bác Thanh khi đó có đưa ra một bài toán của ZingMe (hay MXH nói chung) đó là tính số bạn chung giữa 2 người bất kỳ. Bạn có thể dễ dàng thấy tính năng này khi nhấp vào 1 profile của ai đó, hoặc trên 1 list người dùng facebook như này:

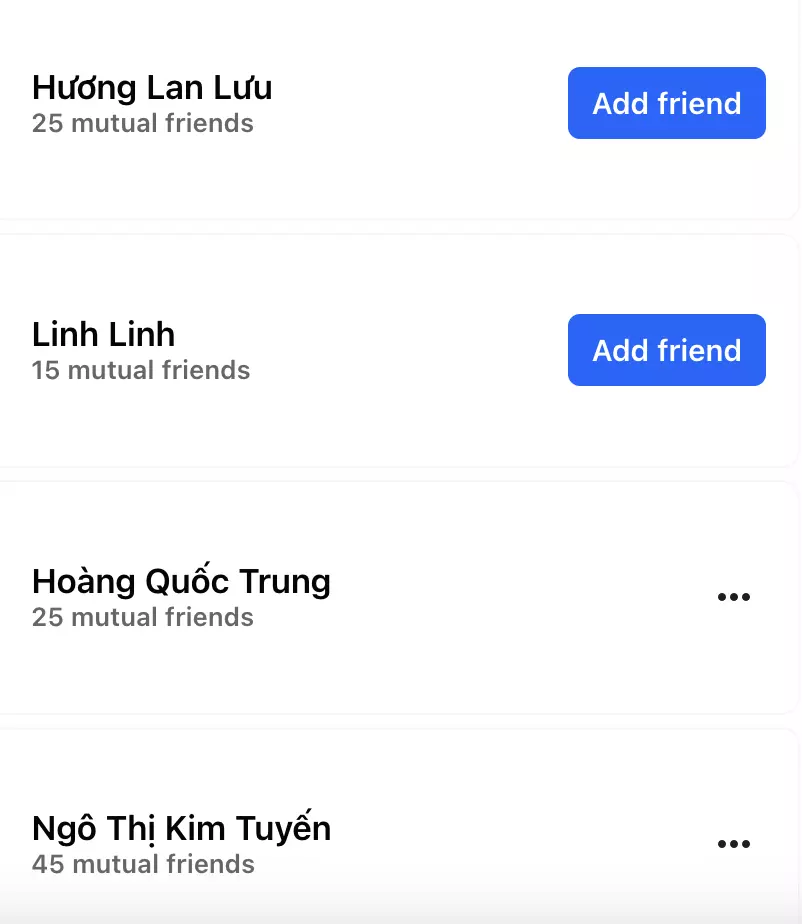
Nhìn thì rất đơn giản, logic cũng không có gì phức tạp cả. Ta có:

• Bạn của User có ID 1 là 1 mảng: [3,5,7,9,11]
• Bạn của User có ID 2 là 1 mảng: [3,4,6,8,11]

~> bạn chung của User 1 và User 2 là User 3 và User 11. Chung quy lại sẽ là bài toán "Tìm phần tử chung (intersection) giữa 2 mảng". Done, đơn giản đúng không?

Thế nhưng nếu như bạn đã từng thử áp dụng bài toán này trong thực tế (hoặc đã từng làm MXH) thì sẽ nhận ra việc tìm phần tử chung của 2 mảng đã rất chậm rồi, nữa là phải tìm phần tử chung của 1 mảng (danh sách bạn bè của mình) với vài chục mảng (danh sách bạn bè của list user hiển thị). Bạn cũng khó mà tính trước để cache sẵn số bạn chung được, bởi bản chất người dùng MXH sẽ tạo thành 1 cái đồ thị (Graph) lớn với vô số đỉnh và vô số cạnh, và tính trước cái đống đấy khá là bất khả thi.

Hãy lấy ví dụ nhỏ nhỏ mà mình đã từng làm đi.

1 MXH G có khoảng 5 triệu user. Để tính trước số bạn chung của mọi user, ta sẽ cần tính:

(5.000.000 * 4.999.999) / 2 ~= 1.249999 x 10^13 (Khoảng hơn 12 nghìn tỷ cặp user)

Không thể tính trước, vậy thì phải tính on-demand, nhưng làm cách nào để nó nhanh và ít tốn tài nguyên?

Solution mà bác Thanh đưa ra là sử dụng Bitset. Ta sẽ tạo ra 2 bitset chứa bạn chung của 2 user như sau:

User 1:

0 0 1 0 1 0 1 0 1 0  1 
│ │ │ │ │ │ │ │ │ │  │ 
1 2 3 4 5 6 7 8 9 10 11

User 2:

0 0 1 1 0 1 0 1 0 0  1 
│ │ │ │ │ │ │ │ │ │  │ 
1 2 3 4 5 6 7 8 9 10 11

Vậy thì mảng bạn chung của 2 user trên sẽ được biểu diễn bằng việc AND (&) 2 bitset trên:

0 0 1 0 1 0 1 0 1 0  1    &    0 0 1 1 0 1 0 1 0 0  1    =    0 0 1 0 0 0 0 0 0 0  1     
│ │ │ │ │ │ │ │ │ │  │         │ │ │ │ │ │ │ │ │ │  │         │ │ │ │ │ │ │ │ │ │  │ 
1 2 3 4 5 6 7 8 9 10 11        1 2 3 4 5 6 7 8 9 10 11        1 2 3 4 5 6 7 8 9 10 11

Vậy, số bạn chung của User 1 và User 2 là 2, đó là User 3 và User 11.

Mấu chốt của cách giải quyết này là việc các phép toán với bit được CPU thực hiện gần như native và cực kỳ nhanh chóng (độ phức tạp thường tương đương O(1)). Nó giống như việc thay vì bảo Tèo - một người không biết tiếng anh - phải tính "One plus Two" và rồi ổng phải đi google xem One là 1, Two là 2, rồi mới tính 1 + 2 = 3 thì giờ hỏi luôn "Một cộng Hai là mấy" ấy.

Điểm yếu lớn nhất của bitset là ở việc nó có thể tốn rất nhiều bộ nhớ. Ví dụ:

Nếu User 3 chỉ có 1 người bạn duy nhất là User 5.000.000 thì sao?

~> Danh sách bạn của User 3:

0 0 0 0 0 ... 0 1
│ │ │ │ │ │ │ │ │ 
1 2 3 4 5 ..... 5000000

Wao, chỗ này ta đã tốn đến 5 triệu bit (625 Kilobyte) chỉ để lưu danh sách 1 phần tử (chỉ là 1 số 4 Byte và chiếm 1 bit). Quá là tốn kém và không hiệu quả.

Để giải quyết vấn đề này thì có nhiều thuật toán nén để tối ưu dung lượng của bitset ra đời như WAH, EWAH, Concise,... tuy nhiên sau này nếu có thể thì mình đều sử dụng một thuật toán khá hiệu quả là Roaring. Đây là thuật toán nén bitmap được rất nhiều tên tuổi lớn như Apache Lucene, Druid, ClickHouse,... tin dùng và được implement rộng rãi trong nhiều ngôn ngữ và các loại database như: CRoaring, Python, Postgres, Redis,...

Các bạn có thể đọc thêm về use case mình đã sử dụng Roaring Bitmap với Redis để blacklist user và post trong MXH như nào trong bài viết: Kỳ án tốc độ: Nỗi oan của chàng Redis

Ngoài ra với bài toán đếm số trong analytic như Analytic cho người nông dân: Bài toán đếm số cũng hoàn toàn có thể sử dụng pg_roaringbitmap để thay thế cho intarray, hỗ trợ intersection và còn cho kết quả chính xác luôn chứ không phải gần đúng như hyperloglog nữa.

Tổng kết

Mặc dù là một kiểu dữ liệu ai cũng biết, hoặc thậm chí người không học IT cũng ít nhiều học qua trong mấy môn tin học đại cương các kiểu rồi, thế nhưng việc trực tiếp ứng dụng bit trong các bài toán thường ngày thì chắc cũng không có nhiều người động tới. Hy vọng bài viết này sẽ đem đến cho các bạn một vài ý tưởng để áp dụng bit trong xử lý những bài toán cần hiệu năng cao. Mình là Minh Monmen, giờ mình lại lặn đây và hẹn gặp lại các bạn trong một bài viết không quá xa nữa.