10 thuật toán học máy mà các kỹ sư cần biết

Không còn nghi ngờ gì nữa, lĩnh vực học máy / trí tuệ nhân tạo (AI) đã ngày càng trở nên phổ biến hơn trong vài năm qua. Một nhánh nhỏ của nó là Big Data đang là xu hướng hot nhất trong ngành công nghệ cao hiện nay, học máy trở nên rất mạnh mẽ để đưa ra các dự đoán hoặc gợi ý được tính dựa trên số lượng lớn dữ liệu. Một số ví dụ phổ biến nhất về học máy là các thuật toán của Netflix để đưa ra các gợi ý về phim dựa trên những bộ phim mà bạn đã xem trong quá khứ hoặc các thuật toán của Amazon đề xuất các sách dựa trên sách mà bạn đã mua trước đây. Những hệ thống gợi ý đó (Recommended System) sẽ giúp ích khá nhiều cho những người dùng trong việc đưa ra những lựa chọn của mình.

Ngoài ra, AI còn có những khả năng như nhận dạng biển số xe tự động, giúp sửa lỗi chính tả, tạo các con robot có khả năng giao tiếp với con người,...Còn nhiều nhiều những khả năng mà AI có thể làm được. AI đang phát triển và sẽ còn phát triển mạnh trong tương lai.

Machine Learning được chia thành 3 nhánh chính: supervised learning (học có giám sát), unsupervised learning (học không có giám sát), và reinforcement learning (học tăng cường).

• Học có giám sát được dùng trong trường hợp một thuộc tính (nhãn) có sẵn cho một tập dữ liệu nhất định (tập huấn luyện), nhưng thiếu và cần được dự đoán cho các trường hợp khác.
• Học không có giám sát thì ngược lại, nó được sử dụng trong trường hợp khám phá các mối quan hệ tiềm ẩn trong một tập dữ liệu không được gán nhãn (các mục không được chỉ định trước).
• Học tăng cường thì nằm giữa 2 loại trên - có một số hình thức phản hồi có sẵn cho mỗi bước tiên đoán hoặc hành động, nhưng không có nhãn chính xác hoặc thông báo lỗi

Dưới đây là 10 thuật toán rơi vào 2 loại đầu tiên, hi vọng vẫn đủ để bạn quan tâm:

Học có giám sát

1. Cây quyết định (Decision Trees)

Cây quyết định là công cụ hỗ trợ quyết định sử dụng biểu đồ dạng cây hoặc mô hình của các quyết định và kết quả có thể xảy ra của chúng, bao gồm kết quả sự kiện ngẫu nhiên, chi phí tài nguyên và lợi ích. Dưới đây là một ví dụ điển hình của cây quyết định:

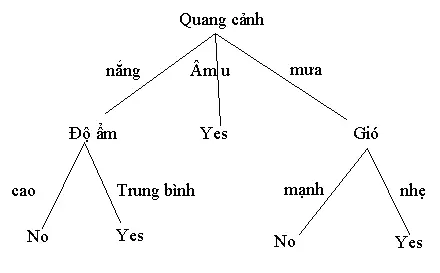
Cây quyết định này cho ta gợi ý về việc có đi đá bóng hay không. Ví dụ, quang cảnh có nắng, độ ẩm trung bình thì tôi sẽ đi đá bóng. Ngược lại, nếu trời mưa, gió mạnh thì tôi sẽ không đi đá bóng nữa.

Cây quyết định tuy là mô hình khá cũ, khá đơn giản những vẫn còn được ứng dụng khá nhiều và hiệu quả. Đứng dưới góc nhìn thực tế, cây quyết định là một danh sách tối thiểu các câu hỏi dạng yes/no mà người ta phải hỏi, để đánh giá xác suất đưa ra quyết định đúng đắn.

2. Phân loại Bayes (Naïve Bayes Classification)

Phân loại Bayes là một nhóm các phân loại xác suất đơn giản dựa trên việc áp dụng định lý Bayes với các giả định độc lập (naïve) giữa các đặc tính.

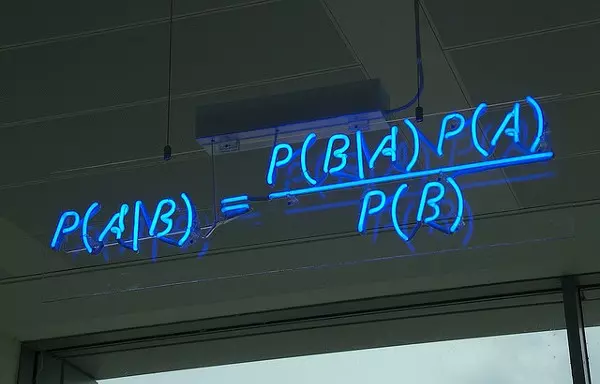
Trong đó: P(A|B) là xác suất có điều kiện A khi biết B, P(A) là xác suất giả thuyết A (tri thức có được về giải thuyết A trước khi có dữ liệu B), P(B|A) là xác suất có điều kiện B khi biết giả thuyết A, P(B) là xác suất của dữ liệu quan sát B không quan tâm đến bất kỳ giả thuyết A nào.

Thuật toán này được áp dụng trong một số bài toán như:

• Đánh dấu một email là spam hay không.
• Phân loại bài viết tin tức thuộc lĩnh vực công nghệ, chính trị hay thể thao.
• Kiểm tra một đoạn văn bản mang cảm xúc tích cực hay tiêu cực.
• Sử dụng cho các phần mềm nhận diện khuôn mặt. ...

3. Hồi quy tuyến tính (Ordinary Least Squares Regression)

Nếu bạn biết thống kê, bạn có thể đã nghe nói về hồi quy tuyến tính trước đây. Bình phương nhỏ nhất là một phương pháp để thực hiện hồi quy tuyến tính. Bạn có thể suy nghĩ về hồi quy tuyến tính như là nhiệm vụ kẻ một đường thẳng đi qua một tập các điểm. Có rất nhiều chiến lược có thể thực hiện được, và chiến lược "bình phương nhỏ nhất" sẽ như thế này - Bạn có thể vẽ một đường thẳng, và sau đó với mỗi điểm dữ liệu, đo khoảng cách thẳng đứng giữa điểm và đường thẳng. Đường phù hợp nhất sẽ là đường mà các khoảng cách này càng nhỏ càng tốt.

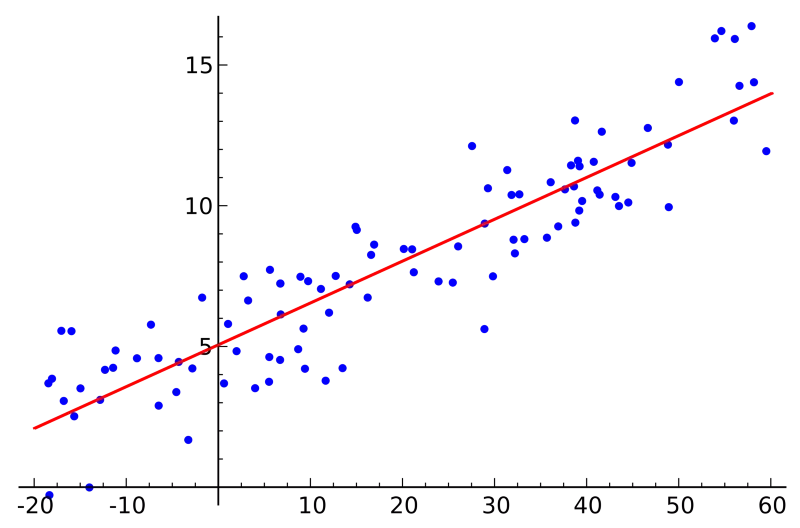
Một số ví dụ là người ta có thể sử dụng mô hình này để dự đoán giá cả (nhà đất, chứng khoán), điểm số,...

4. Hồi quy logistic (Logistic Regression)

Hồi quy logistic là một cách thống kê mạnh mẽ để mô hình hóa một kết quả nhị thức với một hoặc nhiều biến giải thích. Nó đo lường mối quan hệ giữa biến phụ thuộc phân loại và một hoặc nhiều biến độc lập bằng cách ước tính xác suất sử dụng một hàm logistic, là sự phân bố tích lũy logistic.

Thuật toán này được sử dụng trong một số trường hợp:

• Điểm tín dụng ( quyết định có cho khách hàng vay vốn hay không)
• Đo mức độ thành công của chiến dịch marketing
• Dự đoán doanh thu của một sản phẩm nhất định
• Dự đoán động đất ....

5. Support Vector Machines (SVM)

SVM là phương pháp phân loại nhị phân. Cho một tập các điểm thuộc 2 loại trong môi trường N chiều, SVM cố gắng tìm ra N-1 mặt phẳng để phân tách các điểm đó thành 2 nhóm. Ví dụ, cho một tập các điểm thuộc 2 loại như hình bên dưới, SVM sẽ tìm ra một đường thẳng nhằm phân cách các điểm đó thành 2 nhóm sao cho khoảng cách giữa đường thẳng và các điểm xa nhất có thể.

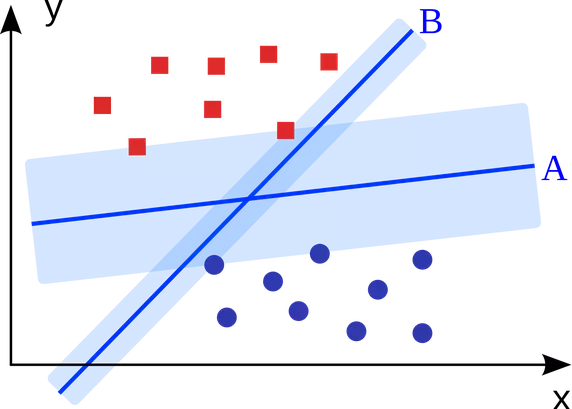
Xét về quy mô, một số vấn đề lớn nhất đã được giải quyết bằng cách sử dụng SVM (với việc thực hiện sửa đổi phù hợp) ví dụ như hiển thị quảng cáo, phát hiện giới tính dựa trên hình ảnh, phân loại hình ảnh có quy mô lớn ...

6. Kết hợp các phương pháp (Ensemble Methods)

Phương pháp này dựa rên sự kết hợp của một vài phương pháp kể trên để dự đoán kết quả, sau đó sẽ đưa ra kết quả cuối cùng dựa vào trọng số của từng phương pháp

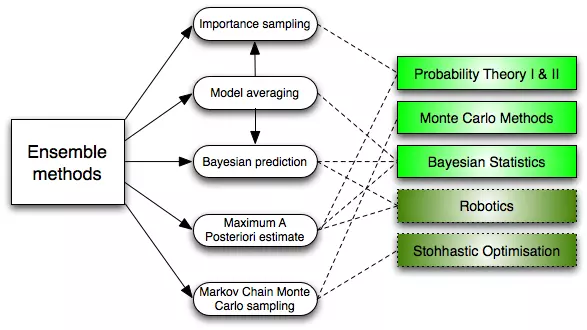
Vậy phương pháp này hoạt động như thế nào và tại sao nó lại ưu việt hơn các mô hình cá nhân?

• Trung bình sai số (bias): một số phương pháp hoạt động tốt và cho sai số nhỏ, ngược lại cũng có một số phương pháp cho sai số lớn. Trung bình ta được một sai số chấp nhận được, có thể nhỏ hơn sai số khi sử dụng duy nhất một phương pháp.
• Giảm độ phụ thuộc vào tập dữ liệu (variance): ý kiến tổng hợp của một loạt các mô hình sẽ ít nhiễu hơn là ý kiến đơn lẻ của một mô hình. Trong lĩnh vực tài chính, đây được gọi là đa dạn hóa - một - một danh mục hỗn hợp của nhiều cổ phiếu sẽ ít biến động hơn so với chỉ một trong số các cổ phiếu riêng lẻ.
• Giảm over-fit: over-fit là hiện tượng khi mô hình hoạt động rất tốt với dữ liệu training, nhưng rất kém đối với dữ liệu test. Việc kết hợp nhiều mô hình cùng lúc giúp giảm vấn đề này.

Học không có giám sát

7. Thuật toán gom cụm (Clustering Algorithms)

Gom cụm là nhiệm vụ nhóm một tập hợp các đối tượng sao cho các đối tượng trong cùng một nhóm (cluster) giống nhau hơn so với các đối tượng trong các nhóm khác.

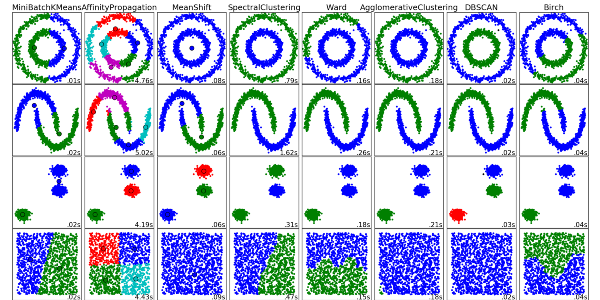
Gom cụm có nhiều phương pháp khác nhau, sau đây là một vài trong số đó:

• Gom cụm dựa vào tâm điểm (Centroid-based algorithms)
• Gom cụm dựa vào tính kết nối (Connectivity-based algorithms)
• Gom cụm dựa vào mật độ (Density-based algorithms)
• Gom cụm dựa vào xác suất (Probabilistic)
• Gom cụm dựa trên giảm chiều dữ liệu (Dimensionality Reduction)
• Gom cụm dựa trên mạng nơ-ron/deep leanring (Neural networks / Deep Learning)

8.Phân tích thành phần chính (Principal Component Analysis - PCA)

PCA là một thuật toán thống kê sử dụng phép biến đổi trực giao để biến đổi một tập hợp dữ liệu từ một không gian nhiều chiều sang một không gian mới ít chiều hơn (2 hoặc 3 chiều) nhằm tối ưu hóa việc thể hiện sự biến thiên của dữ liệu.

Phép biến đổi tạo ra những ưu điểm sau đối với dữ liệu:

• Giảm số chiều của không gian chứa dữ liệu khi nó có số chiều lớn, không thể thể hiện trong không gian 2 hay 3 chiều.
• Xây dựng những trục tọa độ mới, thay vì giữ lại các trục của không gian cũ, nhưng lại có khả năng biểu diễn dữ liệu tốt tương đương, và đảm bảo độ biến thiên của dữ liệu trên mỗi chiều mới.
• Tạo điều kiện để các liên kết tiềm ẩn của dữ liệu có thể được khám phá trong không gian mới, mà nếu đặt trong không gian cũ thì khó phát hiện vì những liên kết này không thể hiện rõ.
• Đảm bảo các trục tọa độ trong không gian mới luôn trực giao đôi một với nhau, mặc dù trong không gian ban đầu các trục có thể không trực giao.

Một số ứng dụng của PCA bao gồm nén, đơn giản hóa dữ liệu để dễ dàng học tập, hình dung. Lưu ý rằng kiến thức miền là rất quan trọng trong khi lựa chọn có nên tiếp tục với PCA hay không. Nó không phù hợp trong trường hợp dữ liệu bị nhiễu (tất cả các thành phàn của PCA đều có độ biến thiên khá cao)

9. Singular Value Decomposition

Trong đại số tuyến tính, SVD là một thừa số của ma trận phức tạp thực sự. Đối với một ma trận m*n đã xác định M, tồn tại một sự phân rã sao cho M = UΣV, trong đó U và V là các ma trận đơn nhất và Σ là một ma trận chéo.

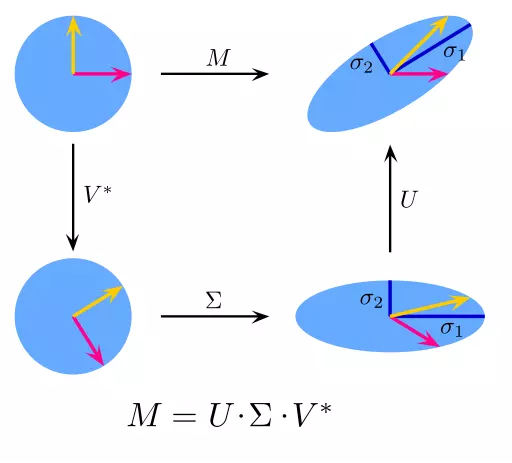
PCA thực ra là một ứng dụng đơn giản của SVD. Trong khoa học máy tính, các thuật toán nhận dạng khuôn mặt đầu tiên được sử dụng PCA và SVD để biểu diễn khuôn mặt như là một sự kết hợp tuyến tính của "eigenfaces", làm giảm kích thước, và sau đó kết hợp khuôn mặt với các tính chất thông qua các phương pháp đơn giản. Mặc dù các phương pháp hiện đại phức tạp hơn nhiều, nhiều người vẫn còn phụ thuộc vào các kỹ thuật tương tự.

10. Phân tích thành phần độc lập (Independent Component Analysis)

ICA là một kỹ thuật thống kê nhằm tìm ra các yếu tố ẩn nằm dưới các bộ biến ngẫu nhiên, các phép đo hoặc tín hiệu. ICA định nghĩa một mô hình phát sinh cho dữ liệu đa biến quan sát được, thường được đưa ra như một cơ sở dữ liệu lớn các mẫu. Trong mô hình, các biến số dữ liệu giả định là hỗn hợp tuyến tính của một số biến tiềm ẩn chưa biết, và hệ thống hỗn hợp cũng không rõ. Các biến tiềm ẩn được giả định không gaussian và độc lập với nhau, và chúng được gọi là các thành phần độc lập của dữ liệu được quan sát.

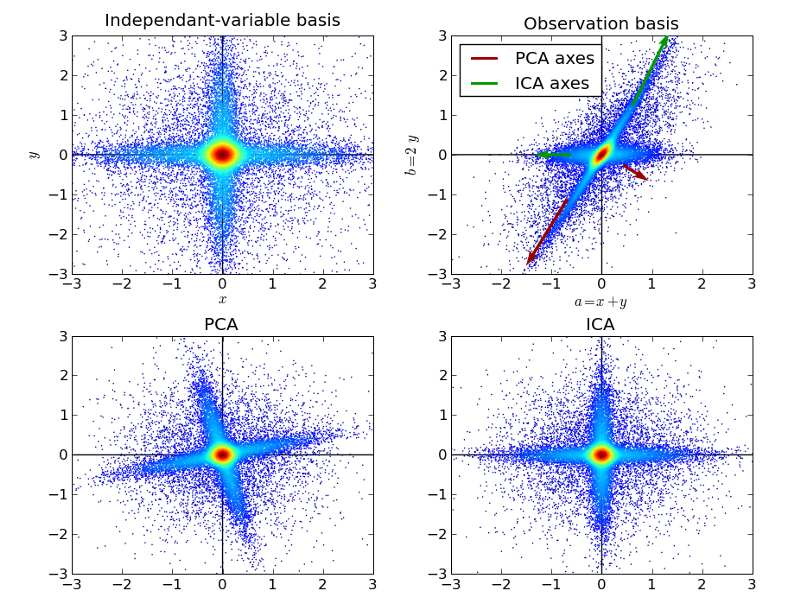
ICA có liên quan đến PCA, nhưng nó là một kỹ thuật mạnh hơn nhiều, có khả năng tìm ra các yếu tố bên dưới của các nguồn trong khi những phương pháp cổ điển thất bại hoàn toàn. Ứng dụng của nó bao gồm hình ảnh kỹ thuật số, cơ sở dữ liệu tài liệu, chỉ số kinh tế và đo lường tâm lý.
Kết thúc bài viết ở đây, hi vọng bạn đọc đã có những cái nhìn tổng quan về các thuật toán phổ biến trong AI. Nếu cảm thấy thích thú, hãy đào sâu hơn về chúng để có thể tạo ra những ứng dụng có "trí tuệ nhân tạo" phục vụ cho mọi người.

Nguồn

1. http://www.kdnuggets.com/2016/08/10-algorithms-machine-learning-engineers.html