Trao đổi khóa Diffie-Hellman trên đường cong Elliptic

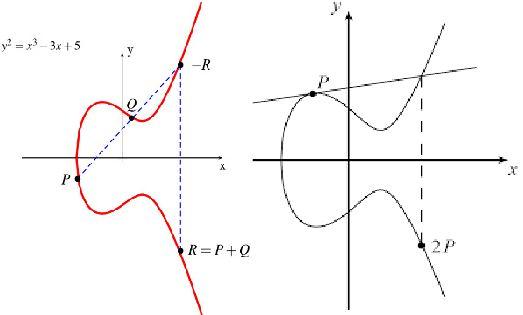
Đường cong Elliptic được định nghĩa có dạng: y^2 = y^3 + ax + b (4a^3 + 27b^2 ≠ 0).

Phép cộng trên đường cong: Cho hai điểm P, Q trên đường cong. Qua P và Q kẻ đường thẳng cắt đường cong E tại điểm thứ ba là R'. Lấy đối xứng R' qua trục hoành được điểm R, khi đó P + Q = R. Trong trường hợp P trùng Q, ta kẻ đường tiếp tuyến tại P và làm tương tự như trên.

Phép nhân vô hướng trên đường cong: Phép nhân vô hướng một số n với một điểm P trên đường cong chính là thực hiện cộng n lần điểm P lại với nhau. VD: 3P = P + P + P.

Trong trường hữu hạn Fp, việc tìm ra giá trị n khi cho trước P, Q và Q = nP là rất khó do độ phức tạp của bài toán Logarit rời rạc. Vì vậy, giả sử Alice và Bob muốn trao đổi khóa cho nhau, họ có thể làm như sau:

Bước 1: Alice và Bob cùng thỏa thuận tham số của đường cong Elliptic như a, b, điểm sinh G, p, ...

Bước 2: Alice chọn giá trị nA làm private key, sau đó tính public key Qa = nAG. Tương tự với Bob, chọn private key nB sau đó tính public key Qb = nBG.

Bước 3: Alice gửi public key của mình là Qa cho Bob và Bob cũng gửi public key của mình là Qb cho Alice.

Bước 4: Alice lấy private key của mình nhân với public key của Bob và ngược lại Bob cũng lấy private key của mình nhân với public key của Alice để ra được khóa chung: sharedKey = nA * Qb = nB * Qa = nA * nB * G.

Mỗi đường cong Elliptic có độ an toàn khác nhau trong việc trao đổi khóa. Do đó, để đảm bảo độ an toàn và thống nhất giữa các bên, người ta tạo ra một số curve phổ biến bao gồm Curve25519, Curve448, secp256k1, NIST P-256, NIST P-384, NIST P-521 … Trong đó, secp256k1 là curve có độ dài khóa 256 bit được ứng dụng trong Bitcoin.