Tôi đã học Assembly 32bit như thế nào (Phần 1)

Mới đầu học thì mình cũng nghĩ rằng Assembly rất khó - "Hiểu thế quái nào được đống EAX EBX kia ???".
Nhưng tin mình đi, Assembly không khó lắm đâu. Ít nhất cho đến bây giờ (mới học được tẹo), mình thấy làm việc với "đống EAX EBX" còn đỡ đau đầu hơn thuật toán nhiều :v

Cùng hít mùi hành với Assembly 32bit nào :v

1. Cài đặt môi trường "học tập"

1.1 Windows

Trên Windows thì có thể cài masm và code trên Visual Studio:

• Link tải masm32: http://www.masm32.com/download.htm
• Link hướng dẫn tạo project asm:

Ngoài Visual Studio ra thì mình thấy IDE SASM cũng khá ổn. Ưu điểm là nhẹ, có thể biên dịch được cả x86 và x64 nếu sau này học lên x64.

• Link tải SASM: https://dman95.github.io/SASM/english.html

Để cho tiện thì khi học Assembly mọi người nên cài IDE để debug cùng 1 chỗ luôn. Theo kinh nghiệm cá nhân mình thì khi mới học mà không có debugger để chạy thì phế 1 nửa.

1.2 Ubuntu

Trên ubuntu thì đơn giản hơn khi gõ 1 lệnh là cài đặt xong nasm luôn (masm cho Windows còn nasm cho Linux).
Mọi người chỉ cần copy đoạn shell script này vào 1 file text, đổi đuôi file thành .sh.

#!/bin/bash
sudo apt install nasm
sudo apt-get install lib32gcc-4.8-dev
sudo apt install gcc-multilib
wget http://download.opensuse.org/repositories/home:/Dman95/xUbuntu_18.04/amd64/sasm_3.10.1_amd64.deb
sudo dpkg -i sasm_3.10.1_amd64.deb

Sau đó chạy lệnh: bash <tên file>.sh

Với các phiên bản ubuntu khác 18.04 thì mọi người thay 18.04 ở link trong lệnh wget thành phiên bản của mình là được. Lưu ý là hiện tại chưa có nasm cho các phiên bản Ubuntu cao hơn 18.04 nhé.

2. Kiến thức nền tảng

Cài xong môi trường rồi thì mọi người cứ để đấy đã, cùng học thêm về các kiến thức nền tảng.
Một số cái chúng ta đã được biết từ trước rồi nhưng chưa kỹ, một số thì mới hoàn toàn. Chúng ta cần phải nắm vững những kiến thức này trước khi bắt tay vào code, hoặc là sẽ vấp phải 1 đống lỗi mà chẳng hiểu tại sao, chẳng biết sửa kiểu gì.
Vì một số kiến thức đã quá phổ thông, nên mình sẽ chỉ nói thêm về những cái bình thường chúng ta ít khi được biết.

2.1 Biểu diễn dữ liệu

Trong Assembly chúng ta có thể biểu diễn dữ liệu dưới các dạng:

• Nhị phân (Binary)
• Thập lục phân (Hex)
• Thập phân (Decimal)
• Bát phân (Octal)

Bốn dạng biểu diễn trên thực ra là để con người nhìn thôi, dù hiển thị ở dạng nào đi nữa thì máy tính cũng sẽ chỉ lưu và làm việc với dữ liệu dưới dạng nhị phân. Thường thì dữ liệu sẽ được hiển thị dưới dạng Hex cho chúng ta xem, vì chuyển từ Bin sang Hex tiện hơn từ Bin sang Dec.

Bạn có biết vì sao các tiền bối lại thiết kế máy tính chuyển từ Bin -> Hex cho chúng ta đọc ?
Mà không phải từ Bin -> Dec, trong khi con người quen làm việc với số thập phân nhất không ?
Đáp án ở cuối bài

Assembly x86 sẽ làm việc với dữ liệu 32bit, khoảng biểu diễn như sau:

Dạng biểu diễn	Min	Max
Dec	-2,147,483,648	2,147,483,647
Bin	11111111 11111111 11111111 11111110	01111111 11111111 11111111 11111111
Hex	80 00 00 00	7F FF FF FF

Nhìn min = 80 00 00 00 còn max = 7F FF FF FF hơi lạ đúng không ? Rõ ràng 7F FF FF FF + 1 = 80 00 00 00 mà ?
Yên tâm, đó là do cách máy tính biểu diễn với số có dấu.

2.2 Biểu diễn số nguyên có dấu trong máy tính

2.2.1 Phương pháp dấu lượng

Trong phương pháp dấu lượng, bit đầu tiên bên trái (MSB - Most Significant Bit) được sử dụng làm bit dấu. Nếu là số dương thì bit dấu = 0, còn số âm thì bit dấu = 1.

Các bit còn lại sẽ được dùng để biểu diễn giá trị. Như vậy khoảng giá trị có thể biểu diễn sẽ chỉ còn -2^(n - 1) --> 2^(n - 1) - 1.

VD:

• Số 5 trong hệ nhị phân: 00000101
• Số -5 trong hệ nhị phân: 10000101

Cách biểu diễn này có 1 điểm chưa nhất quán, đó là số 0 sẽ có 2 cách biểu diễn là 00000000 (+0) và 10000000 (-0)

Phương pháp này được các máy tính thế hệ đầu tiên như IBM sử dụng.

2.2.2 Phương pháp bù 1

Phương pháp bù 1 tương tự phương pháp dấu lượng, chỉ khác ở cách biểu diễn độ lớn của số:

• Nếu là số dương thì bit dấu = 0
• Nếu là số âm thì đảo các bit giá trị, bit dấu = 1

VD:

• Số 5 trong hệ nhị phân: 00000101
• Số -5 trong hệ nhị phân: 11111010

Với phương pháp bù 1 thì số 0 vẫn có 2 cách biểu diễn là 00000000 (+0) và 11111111 (-0)

Khi thực hiện phép cộng với số nhị phân bù 1, nếu sau khi cộng bit nhớ = 1 thì phải cộng thêm bit nhớ vào kết quả vừa thu được. Điều này bất tiện khi máy tính thực hiện các phép toán.

Phương pháp bù 1 được các máy tính thế hệ cũ như PDP, UNIVAC sử dụng.

2.2.3 Phương pháp bù 2

Phương pháp bù 2 đã có sự cải tiến nhằm thuận tiện hơn trong việc tính toán với số nhị phân, cụ thể:

• Nếu là số dương thì bit dấu = 0
• Nếu là số âm thì bit dấu = 1, đảo các bit giá trị sau đó cộng thêm 1 vào kết quả.

Cách biểu diễn bù 2 ra đời nhằm khắc phục 2 vấn đề của phương pháp dấu lượng và phương pháp bù 1:

• Số 0 có 2 cách biểu diễn
• Bit nhớ phát sinh sau khi đã thực hiện phép tính phải được cộng tiếp vào kết quả

Việc đổi dấu 1 số từ âm <==> dương đều được thực hiện theo 1 cách duy nhất: đảo tất cả các bit và cộng thêm 1.
Khi thực hiện phép cộng với số bù 2, nếu phát sinh bit nhớ ở bit dấu, ta có thể bỏ nó đi.

Hiện nay các máy tính hiện đại sử dụng phương pháp bù 2.

2.2.4 Bù 2 với hệ cơ số 16

Bù 2 trong hệ cơ số 16 không có gì thay đổi, vẫn là đảo tất cả các bit và cộng thêm 1. Việc đảo bit trong Hex rất đơn giản, chỉ cần trừ mỗi ký tự Hex đi 15:

6A3D --> 95C2 + 1 --> 95C3
95C3 --> 6A3C + 1 --> 6A3D

2.3 Kích thước lưu trữ

Đơn vị lưu trữ dữ liệu cơ bản của các máy tính 32bit là byte có kích thước 8bit. Trên byte còn có word (2 bytes), doubleword (4 bytes) và quadword (8 bytes).

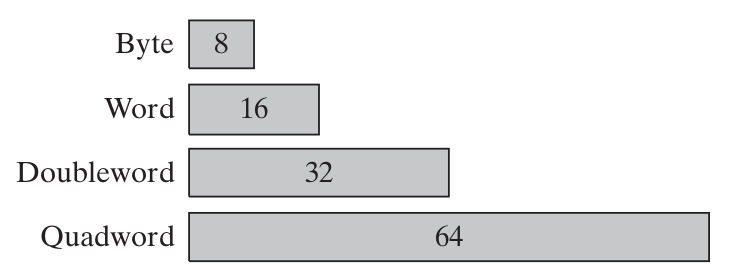
Khoảng biểu diễn của chúng như sau:

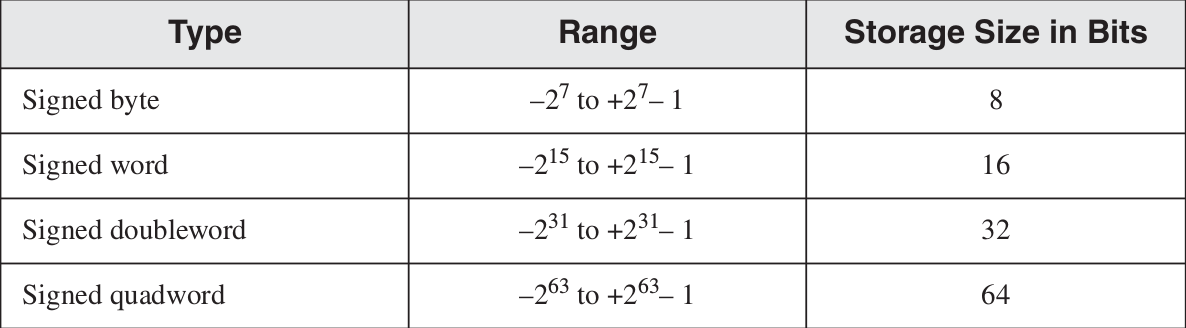
2.4 Biểu diễn xâu

String trong máy tính được biểu diễn bằng 1 mảng các giá trị tương ứng với ký tự đó trong bảng ASCII. Thường thì sẽ viết dưới dạng Hex, ít người viết dưới dạng thập phân.
VD: xâu “ABC123” có thể hiển thị dưới dạng 41h, 42h, 43h, 31h, 32h, 33h.

2.5 Biểu thức đại số Boolean

Có 4 biểu thức boolean sau:

• AND
• OR
• NOT
• XOR

Những biểu thức này quá cơ bản rồi nên mình sẽ không đề cập thêm chi tiết nữa. Trong Assembly thì những biểu thức này sẽ được sử dụng nhiều. VD như: sử dụng AND để lập bit, XOR để xóa bit, .... và nhiều công dụng hay ho khác mà chúng ta sẽ không biết nếu không học Assembly :3

---

Đáp án: https://viblo.asia/p/vi-sao-chung-ta-thuong-su-dung-hex-nhieu-hon-dec-Ljy5V77zKra