Thuật toán Minimax (AI trong Game)
Bài đăng này đã không được cập nhật trong 2 năm
Vừa qua mình có làm game dạng như caro và đã làm AI cho nó có dùng thuật toán minimax thấy hay hay nên post lên chia sẻ cho mọi người cùng tham khảo. Bài viết này mình chỉ viết về những cái cơ bản của thuật toán có thể áp dụng cho những game đơn giản dạng này như caro, tictactoe..
Phần mở đầu sơ qua thế là xong. Và bây giờ là bắt đầu nào. 
- Thuật toán minimax là gì? Minimax là giải thuật là một thuật toán đệ quy lựa chọn bước đi kế tiếp trong một trò chơi có hai người bằng cách định giá trị cho các Node trên cây trò chơi sau đó tìm Node có giá trị phù hợp để đi bước tiếp theo.
- Tại sao phải cần dùng minimax? Như các bạn đã biết thì có rất nhiều thuật toán tìm kiếm để làm AI trong game như A, Heuristic... Mỗi thuật toán thì sẽ phù hợp với từng loại game cho nó. Những game đối kháng trong đối người chơi luân phiên đánh như cờ vua, cờ tường, caro... Khi chơi bạn có thể khai triển hết không gian trạng thái nhưng khó khăn chủ yếu là bạn phải tính toán được phản ứng và nước đi của đối thủ mình như thế nào? Cách xử lý đơn giản là bạn giả sử đối thủ của bạn cũng sử dụng kiến thức về không gian trạng thái giống bạn. Giải thuật Minimax áp dụng giả thuyết này để tìm kiếm không gian trạng thái của trò chơi. Trường hợp này thuật toán minimax sẽ đáp ứng những gì mình cần.
- Các khái niệm
- Cây trò chơi (Game tree) - Đại khái là một sơ đồ hình cây thể hiện từng trạng thái, từng trường hợp của trò chơi theo từng nước đi.
- Mỗi node biểu diễn 1 trạng thái của trò chơi hiện tại trên cây trò chơi.
- Node được gọi nút lá là tại đó trò chơi kết thúc (trạng thái trò chơi lúc đó có thể thắng, thua hoặc hòa).
- Giải thuật Minimax Hai người chơi trong game được đại diện là MAX và MIN. MAX đại diện cho người chơi luôn muốn chiến thắng và cố gắng tối ưu hóa ưu thế của mình còn MIN đại diện cho người chơi cố gắng cho người MAX giành số điểm càng thấp càng tốt. Giải thuật Minimax thể hiện bằng cách định trị các Node trên cây trò chơi: Node thuộc lớp MAX thì gán cho nó giá trị lớn nhất của con Node đó. Node thuộc lớp MIN thì gán cho nó giá trị nhỏ nhất của con Node đó. Từ các giá trị này người chơi sẽ lựa chọn cho mình nước đi tiếp theo hợp lý nhất.
Giờ mình đi vào ví dụ để dễ hiểu như khái niệm ở trên. Game TicTacToe
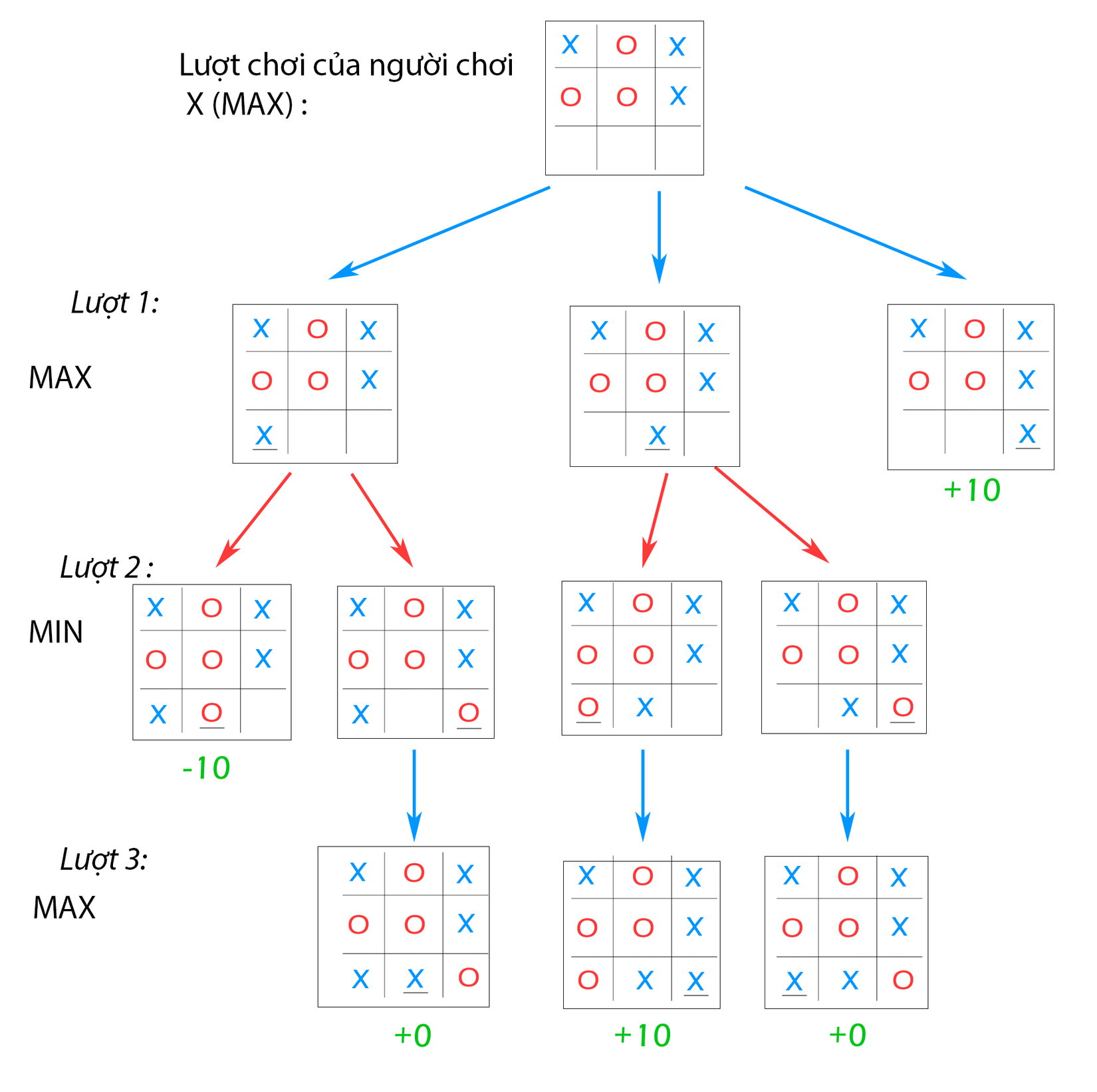 Như hình trên ta thấy là trạng thái hiện tại của game đang đến lượt đánh của người chơi X đại diện cho MAX. Ta tạm quy định giá trị MAX lúc game thắng cho X = +10 và MIN lúc game thua cho X = -10 và lúc game hòa = 0. Lúc này ở lượt 1, MAX có thể đi được 1 trong 3 nước như hình. Vậy làm sao để chọn 1 trong 3 nước đó nước nào là tốt nhất để đi. Chúng ta dựa vào giá trị của từng nước để chọn nước tốt nhất, như ở đây 3 node đó thuộc lớp MAX nên chọn giá trị lớn nhất. Chúng ta bắt đầu tìm giá trị của từng node đó. Ở lớp MAX trong lượt 1, thì ta có node 1,2,3 được đánh số từ trái sáng phải như hình. Node 3 chúng ta đã là node lá (X win game ) và có giá trị là +10. Còn 2 node 1,2 thì chưa biết giá trị của nó tại lượt 1 nên chúng ta dựa vào giá trị của các node con để định giá trị và bằng giá trị bé nhất của các node con ở lớp MIN tại lượt 2. Cứ tiếp tục tương tự như vậy đến lúc gặp node lá thì từ node lá đó ta suy ngược lại và ta tính được node 1 có giá trị là -10 và node 2 là 0. Vậy nước đi tốt nhất ở đây là như node 3 có giá trị lớn nhất là +10.
5. Áp dụng vào code
Như hình trên ta thấy là trạng thái hiện tại của game đang đến lượt đánh của người chơi X đại diện cho MAX. Ta tạm quy định giá trị MAX lúc game thắng cho X = +10 và MIN lúc game thua cho X = -10 và lúc game hòa = 0. Lúc này ở lượt 1, MAX có thể đi được 1 trong 3 nước như hình. Vậy làm sao để chọn 1 trong 3 nước đó nước nào là tốt nhất để đi. Chúng ta dựa vào giá trị của từng nước để chọn nước tốt nhất, như ở đây 3 node đó thuộc lớp MAX nên chọn giá trị lớn nhất. Chúng ta bắt đầu tìm giá trị của từng node đó. Ở lớp MAX trong lượt 1, thì ta có node 1,2,3 được đánh số từ trái sáng phải như hình. Node 3 chúng ta đã là node lá (X win game ) và có giá trị là +10. Còn 2 node 1,2 thì chưa biết giá trị của nó tại lượt 1 nên chúng ta dựa vào giá trị của các node con để định giá trị và bằng giá trị bé nhất của các node con ở lớp MIN tại lượt 2. Cứ tiếp tục tương tự như vậy đến lúc gặp node lá thì từ node lá đó ta suy ngược lại và ta tính được node 1 có giá trị là -10 và node 2 là 0. Vậy nước đi tốt nhất ở đây là như node 3 có giá trị lớn nhất là +10.
5. Áp dụng vào code
- Đầu tiên chúng ta cần 1 hàm để biết trạng thái game hiện tại đã thắng, thua hay hòa.
CheckStateGame(Move) - Tiếp theo là cần tìm nước tốt nhất cần đi.
function findBestMove(board):
bestMove = NULL
for each move in board :
if current move is better than bestMove
bestMove = current move
return bestMove
- Và tiếp đến là hàm tính giá trị minimax của các nước đó.
function minimax(board, isMaximizingPlayer):
if(CheckStateGame(curMove) == WIN_GAME)
return MAX
if(CheckStateGame(curMove) == LOSE_GAME)
return MIN
if( CheckStateGame(curMove) == DRAW_GAME)
return DRAW_VALUE
if isMaximizingPlayer :
bestVal = -INFINITY
for each move in board :
value = minimax(board, false)
bestVal = max( bestVal, value)
return bestVal
else :
bestVal = +INFINITY
for each move in board :
value = minimax(board, true)
bestVal = min( bestVal, value)
return bestVal
Vậy là chúng ta implement được thuật toán minimax.
6. Thuật toán Minimax với độ sâu
 Như ở hình này ta cần tìm giá trị lớn nhất của các node con. Mà ta tính được giá trị node 1,2,3 tương ứng là -10, +10, +10. Vậy giá trị ở node 2,3 là bằng nhau = +10. Nên ta đang phân vân giữa 2 node 2,3.
Từ đó ta nâng cấp thuật toán minimax với độ sâu depth:
Như ở hình này ta cần tìm giá trị lớn nhất của các node con. Mà ta tính được giá trị node 1,2,3 tương ứng là -10, +10, +10. Vậy giá trị ở node 2,3 là bằng nhau = +10. Nên ta đang phân vân giữa 2 node 2,3.
Từ đó ta nâng cấp thuật toán minimax với độ sâu depth:
function minimax(board, depth,isMaximizingPlayer):
if(CheckStateGame(curMove) == WIN_GAME)
return MAX - depth
if(CheckStateGame(curMove) == LOSE_GAME)
return MIN + depth
if( CheckStateGame(curMove) == DRAW_GAME)
return DRAW_VALUE
if isMaximizingPlayer :
bestVal = -INFINITY
for each move in board :
value = minimax(board, depth +1, false)
bestVal = max( bestVal, value)
return bestVal
else :
bestVal = +INFINITY
for each move in board :
value = minimax(board, depth + 1,true)
bestVal = min( bestVal, value)
return bestVal
Áp dụng nâng cấp trên thì ta sẽ có giá trị mới của node 1,2,3 tương ứng là -9,+8,+10 => Max = +10 giá trị của node 3. Vậy node 3 là node cần tìm.
7. Tối ưu thuật toán minimax
Đánh giá thuật toán: Giả sử số nhánh của cây game là a. Xét độ sâu depth b thì số nút cần phải tính là a^b. Đây là con số khá lớn.
Nên sinh ra thuật toán để tối ưu thuật toán minimax là cắt tỉa Alpha Beta. (Sẽ được update vào các bài sau  ).
).
Và bài viết mình đến đây cũng đã khá dài. Mình xin kết thúc bài này tại đây.
All rights reserved