Khai bút đầu xuân bằng cách điểm lại vài kiến thức cơ bản :vvvv

Hẳn những ai làm quen với Machine Learning và AI, và kể cả những người chưa từng tiếp xúc, và cả những người ngoài ngành IT này nữa, đều ít nhiều từng biết đến các AI tự vẽ tranh, tự chơi nhạc, tự viết text, hay nói đúng hơn là tự sinh (generative). trong những năm trở lại đây, các mô hình sinh đã đạt được những bước tiến vô cùng đáng kể và tạo ra nhiều giá trị chân thực. Nhắc đến họ mô hình sinh generative models, tất nhiên phải kể đến hai cái tên phổ biến nhất và được quan tâm nhất là các mô hình GAN (Generative Adversarial Networks) và Variational Autoencoders (VAEs).

Các mục trong bài viết bao gồm:

• #1 Mô hình Autoencoder
• #2 Mối liên hệ giữa Autoencoder và PCA trong vấn đề giảm chiều dữ liệu
• #3 Variational Autoencoder cải tiến những gì so với Autoencoder cơ bản

Đây là một bài viết dài dài (tản mạn mà ) Nếu muốn nhanh chóng, bạn có thể lướt thẳng đến từng phần mong muốn.

Trước khi đi vào VAE, mình muốn nhắc lại một chút về Autoencoder và PCA.

1. Nhắc lại Autoencoder

Nếu bạn chưa từng nghe về AutoEncoder, đừng ngại lý thuyết dài dòng, click vào đây và bạn có thể hiểu ngay ý tưởng cơ bản của Auto Encoder là làm gì trong vài phút. Nhìn chung, ý tưởng xuất phát của Autoencoder khá đơn giản.

• Autoencoder In PyTorch - Theory & Implementation.

P/s: Mình thích cái video này vì chủ video là dân engineer nên cách tiếp cận khá chi là thoải mái :vv Và giọng tiếng anh dễ nghe nữa.

Autoencoder gồm 3 phần

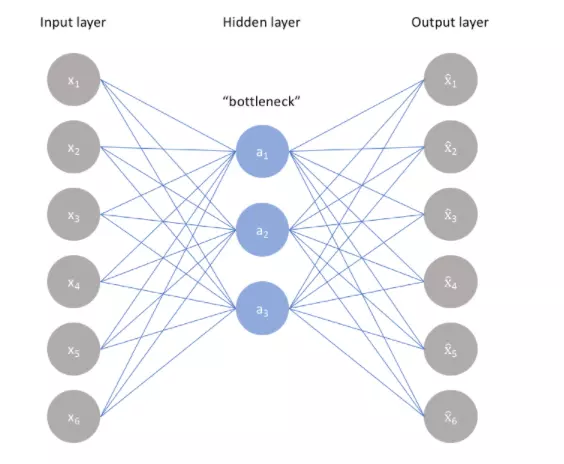
• Encoder: chúng ta có một cái ảnh. Ví dụ ảnh 128x128x 3 channel màu RGB, và ta thấy lưu hơi mất nhiều không gian. Nên chúng ta cần một không gian nhỏ hơn để chứa ảnh. Vậy chúng ta sẽ lấy ra những đặc trưng của cái ảnh đó, bỏ đi những thứ ko cần thiết, sau đó nén nó vào một cái vecto đặc trưng với ít chiều hơn ban đầu. Đó là điều mà phần Encoder đang cố gắng làm.

• Botteneck: vecto đặc trưng đã nói ở trên, nơi chứa các thông tin quan trọng đã được cô đọng của đầu vào. Bởi thế nên có thể rút ra một vài điều:

• (1) chiều của bottelneck chắc chắn phải nhỏ hơn chiều đầu vào và

• (2) Bottleneck càng nhỏ, càng giảm overfitting vì mô hình sẽ phải chọn lọc các thông tin quan trọng hơn để đem theo, không có khả năng ôm đồm quá nhiều và

• (3) Bottelneck nhỏ quá, lưu được quá ít thông tin, khiến Decoder giải mã không ra. Rốt cuộc thì, cái gì Balance cũng mới tốt =))))

  Từ phần sau, mình sẽ gọi nó là latent space (không gian tiềm ẩn).

• Decoder: Giải mã ngược từ bottleneck để cố gắng tạo ra một cái ảnh mới có liên quan chặt chẽ với ảnh cũ (đương nhiên rồi nó chứa các thông tin quan trọng của ảnh cũ mà =))). Liên quan chặt chẽ đến mức nào thì bạn có thể nhìn vào hàm loss, hàm so sánh giữa ảnh mới và ảnh cũ. Trong AE hàm loss được gọi là reconstruction loss. Như có thể thấy trong video trên, reconstruction loss được sử dụng là MSELoss. Có thể thay bằng L1 Loss, còn nếu input là categorical thì dùng Cross Entropy Loss.

Khoan đã dừng khoảng chừng là 5s. Thế có khác gì cố gắng tạo ra ảnh mới như ảnh cũ, Là copy paste hay gì?

Đúng vậy, nếu bạn đã xem video trên thì sẽ thấy ảnh mới có nội dung y như ảnh cũ. Đúng vậy, điều mà Autoencoder đang cố gắng làm là tái hiện lại nội dung cũ, nhưng với những giá trị pixel mới =))))) Trong thực tế, một autoencoder là một tập hợp các hạn chế buộc mạng phải tìm hiểu những cách thức mới để đại diện cho dữ liệu mà không làm thay đổi nội dung của nó.

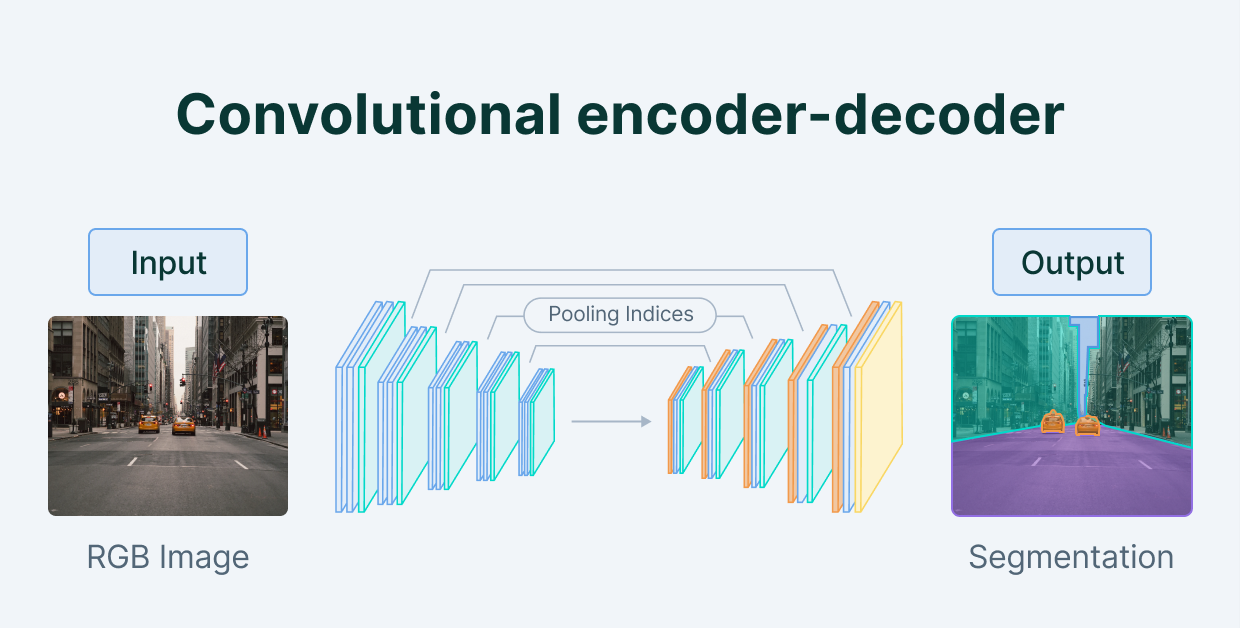
Vậy Autoencoder được dùng làm gì?

Nhìn sơ qua có thể thấy ngay vài ứng dụng:

• Giảm chiều dữ liệu
• Tạo data mới (nên mới được gọi là mô hình sinh =)))
• Khử nhiễu: bởi vì điều mà mô hình đang cố làm chính là giữ lại những gì tổng quát và quan trọng, nên việc khéo léo bỏ đi những chi tiết không liên quan chính là một phần của việc khử nhiễu. Thậm chỉ không chỉ dùng để khử nhiểu ảnh, mà còn có thể khử tiếng ồn noisy trong âm tranh chẳng hạn. Đọc thêm về Denoising Autoencoder (DAE). Hoặc bạn có thể đầy đủ 5 loại AutoEncoder phổ biến tại phần tài liệu tham khảo cuối bài.

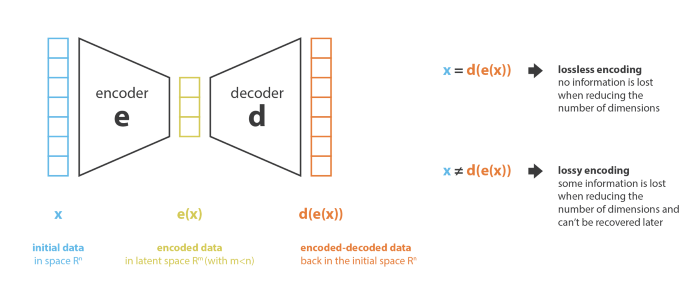
Như hình ảnh trên, với đầu vào $x$, sau khi đi qua bộ mã hóa $E$ và bộ giải mã $D$, ta thu được $d(e(x))$. Mục tiêu là tìm $(e^*, d^*)\in(E \times D)$ sao cho

$$(e^*, d^*)=\underset{(e, d) \in E \times D}{argmin} (error(x, d(e(x))))$$

Từ đây mình gọi $N$ là số data, $n_d$ là số chiều dữ liệu ban đầu và $n_e$ là số chiều dữ liệu sau khi encode. (latent dimension).

Triển khai code

Code có thể được triển khai rất đơn giản trên PyTorch như sau:

import torch

import torch.nn.functional as F

class Encoder(torch.nn.Module):
 def __init__(self, latent_dim=128):
   super(Encoder, self).__init__()
   self.enc1 = torch.nn.Linear(128x128, 512) # input image shape: (3,128,128)
   self.mean_x = torch.nn.Linear(512,latent_dim)
   self.logvar_x = torch.nn.Linear(512, latent_dim)
   
 def forward(self,inputs):
   x = self.enc1(inputs)
   x= F.relu(x)
   z_mean = self.mean_x(x)
   z_log_var = self.logvar_x(x)
   return z_mean, z_log_var

Và Decode:

class Decoder(torch.nn.Module):
 def __init__(self, latent=128):
   super(Decoder, self).__init__()
   self.dec1 = torch.nn.Linear(latent, 512)
   self.out = torch.nn.Linear(512, 128x128)


 def forward(self,z):
   z = self.dec1(z)
   z = F.relu(z)
   return self.out(z)

Năm loại Autoencoder phố biến

• Undercomplete autoencoders
• Sparse autoencoders
• Contractive autoencoders
• Denoising autoencoders
• Variational Autoencoders (for generative modelling)

Tìm đọc đầy đủ tại tài liệu ở phần 6.

Tiếp theo, hãy nghía qua PCA một chút.

2. Autoencoder và mối liên hệ với PCA

Ở phía trên, mình có nhắc đến dùng Autoencoder để giảm chiều dữ liệu (Dimensionality Reduction).

Nhắc tới các thuật toán Dimensionality Reduction, không thể không nhắc tới một trong những thuật toán cơ bản nhất là Principal Component Analysis (PCA) (Phân tích thành phần chính). Phương pháp này dựa trên quan sát rằng dữ liệu thường không phân bố ngẫu nhiên trong không gian mà thường phân bố gần các đường/mặt đặc biệt nào đó.

Hử, hình như hơi trừu tượng. Vậy ta có ngay một ví dụ.

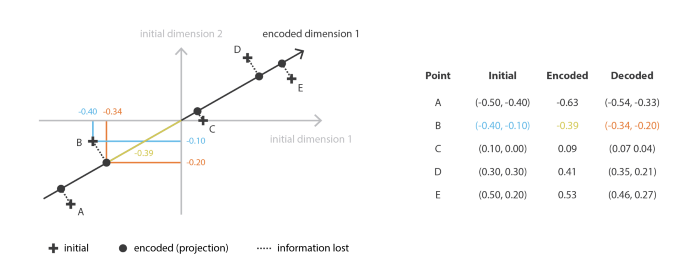
Trong hình trên, ta đặt các điểm đang cố gắng encode các điểm dữ liệu A, B, C ở dạng 2 chiều nén về còn một chiều. Điều này là có thể bởi vì các điểm dữ liệu có vẻ như đang phân bố gần một đường nào đó. Sau đó đưa về một đường thẳng (tuyến tính).

Ở trên, mình cũng có nhắc đến việc Encoder sẽ cố giữ lại những thông tin quan trọng. Vậy nếu, tất cả mọi thông tin đều có vẻ quan trọng như nhau, thì giữ lại cái nào?

Hẳn bạn sẽ nói, làm gì có chuyện mọi thông tin đều quan trọng như nhau. Vậy mình xin phép sửa lại câu hỏi trên như sau: nếu đến một thời điểm nào đó, mọi giá trị đều mang thông tin như nhau. Bạn muốn nén bottleneck chỉ là một vecto 128 chiều, nhưng vẫn còn khoảng 200 giá trị mà bỏ cái nào đi cũng làm mất thông tin quan trọng.

Vậy phải làm sao?

Bài viết về PCA trên forum Machine learning cơ bản đã nêu ra một ví dụ khá dễ hiểu. Giả sử ta có 4 camera lắp ở bốn góc phòng. Vai trò như nhau nên camera nào cũng quan trọng. Nhưng nếu đặt trong hoàn cảnh, một người đang đi về hướng 1 camera, dùng hệ quy chiếu là một đường thẳng đi qua 2 camera và người, thì lúc này chắc chắn hình ảnh camera đó thu được (khuôn mặt) sẽ hữu ích hơn nhiều so với các camera còn lại (chỉ thấy gáy và tóc). Vậy đặt trong một trường hợp cụ thể, mức độ quan trọng 4 camera đã khác nhau.

Vậy mấu chốt là, thử đặt trong một hệ quy chiếu khác đi, mức độ quan trọng của các thông tin sẽ thay đổi.

Nói theo kiểu Toán hơn một chút (From Machine Learning cơ bản)

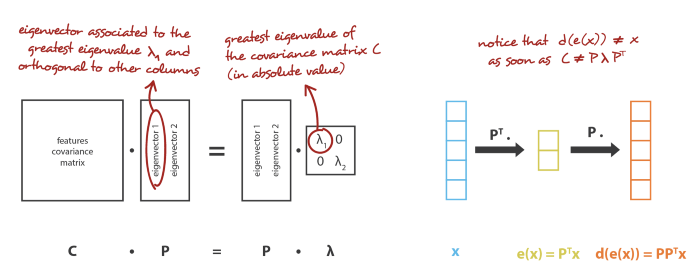
PCA chính là phương pháp đi tìm một hệ cơ sở mới sao cho thông tin của dữ liệu chủ yếu tập trung ở một vài toạ độ, phần còn lại chỉ mang một lượng nhỏ thông tin. Và để cho đơn giản trong tính toán, PCA sẽ tìm một hệ trực chuẩn để làm cơ sở mới.

Mọi chi tiết toán học về PCA có thể tìm thấy tại ML cơ bản - Bài 27: Principal Component Analysis (phần 1/2) Hình như hơi lan man rồi, quay về chủ đề chính thôi.

Vậy PCA liên quan gì ở đây?

Như đã thấy ở trên, PCA cố gắng chuyển dữ liệu từ high-dimensional về một hyperplane thấp hơn. Chính nó, chính là điều mà phần Encoder cũng đang cố làm.

Nhưng dễ thấy, PCA chỉ xây dựng các mối quan hệ tuyến tính.

Trong khi đó, với việc thêm các Activation function vào mạng neural làm Autoencoder có khả năng học các mối quan hệ phi tuyến. Nếu bỏ các hàm này đi, AE giờ có thể chỉ coi ngang như PCA.

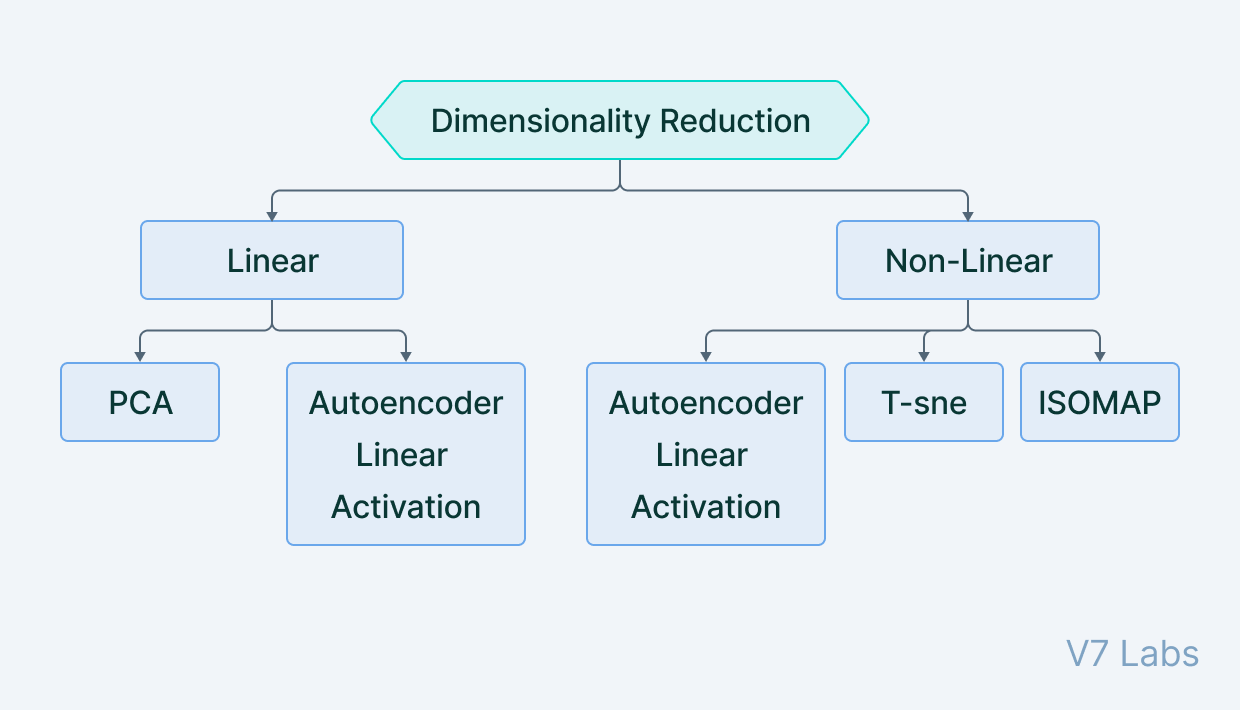
Mối liên hệ giữa PCA và Autoencoder được thể hiện ở hình dưới.

Tản mạn thế đủ rồi. Hãy vào phần chính của bài viết hôm nay :vvv

3. Variational Autoencoders (VAEs)

Ở phần đầu, mình đã nhắc đến việc ảnh mới được tạo từ Autoencoder có liên quan chặt chẽ đến ảnh cũ. Thế nào là liên quan chặt chẽ? Thực ra có một câu hỏi lớn hơn, Autoencoder có gì không tốt?

Paper gốc:

• An Introduction to Variational Autoencoders

Một số thuật ngữ

• latent space: không gian tiềm ẩn (chỉ vùng bottleneck) (chẳng biết dịch thế nào cho chuẩn =))))
• latent dimension: chiều dữ liệu sau khi encode
• Tính liên tục continuity: hai điểm gần nhau trong không gian tiềm tàng không được cung cấp hai nội dung hoàn toàn khác nhau sau khi được giải mã
• Tính đầy đủ completeness: đối với một phân phối đã chọn , một điểm được lấy mẫu từ không gian tiềm ẩn sẽ cung cấp nội dung "có ý nghĩa" sau khi được giải mã
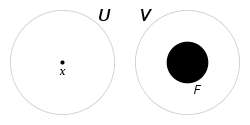
• Regular space: được định nghĩa là, nếu có tập bao đóng F, xét bất ký điểm x nào không thuộc F, luồn tồn tại lân cận U của x và V của F không trùng nhau (tách rời nhau). Tại đây, bất kỳ hai điểm nào có thể phân biệt được về mặt cấu trúc liên kết đều có thể được phân tách bằng các vùng lân cận.

Hạn chể của AE

Vấn đề được chỉ ra ở Autoencoder là kể cả khi latent dimension thấp, mạng vẫn có thể tận dụng mọi khả năng một cách quá mức (overfitting). Mục tiêu duy nhất của nó là giảm loss xuống mức thấp nhất, bỏ qua mọi điều còn lại như giữa nguyên phân phối, abc vv... Khi đó, không gian tiềm ẩn của một bộ mã tự động có thể cực kỳ bất thường, dẫn đến:

• Mất tính liên tục: các điểm gần trong không gian tiềm ẩn có thể cung cấp dữ liệu được giải mã rất khác nhau
• Mất tính đầy đủ: Một số điểm của không gian tiềm ẩn có thể cung cấp nội dung vô nghĩa sau khi được giải mã,…

Vậy, nếu chúng ta không cẩn thận về định nghĩa của kiến trúc, hiển nhiên mạng sẽ tận dụng mọi khả năng quá mức để đạt được nhiệm vụ của nó. Đó là lý do ta nên quy định nó một cách rõ ràng từ trước.

• Đó là lý do cần đến Variational Autoencoders (VAEs).

Ý tưởng chính

Thay vì mã hóa (encode) đầu vào như một điểm duy nhất, ta mã hóa nó dưới dạng phân phối trên không gian tiềm ẩn.

Hình ảnh dưới đây mô tả sợ khác nhau giữa AE và VAE.

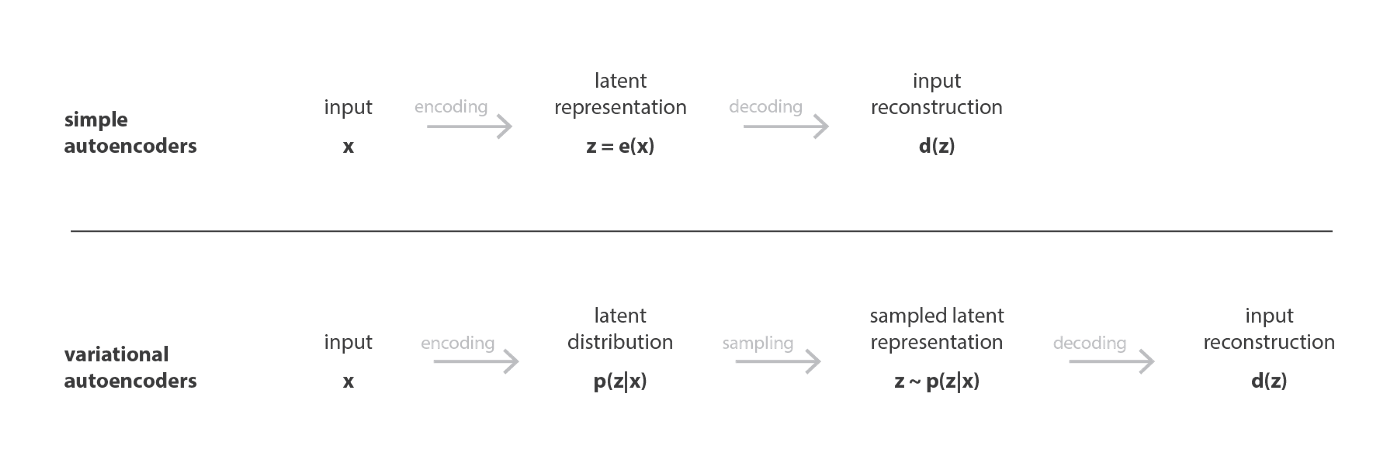
Cụ thể hơn một chút nữa về điều thực sự diễn ra ở latent space.

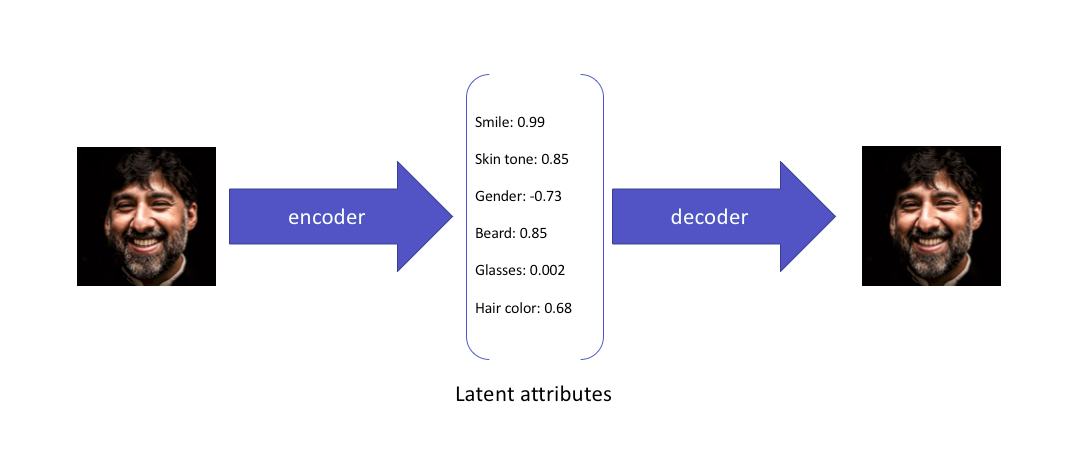
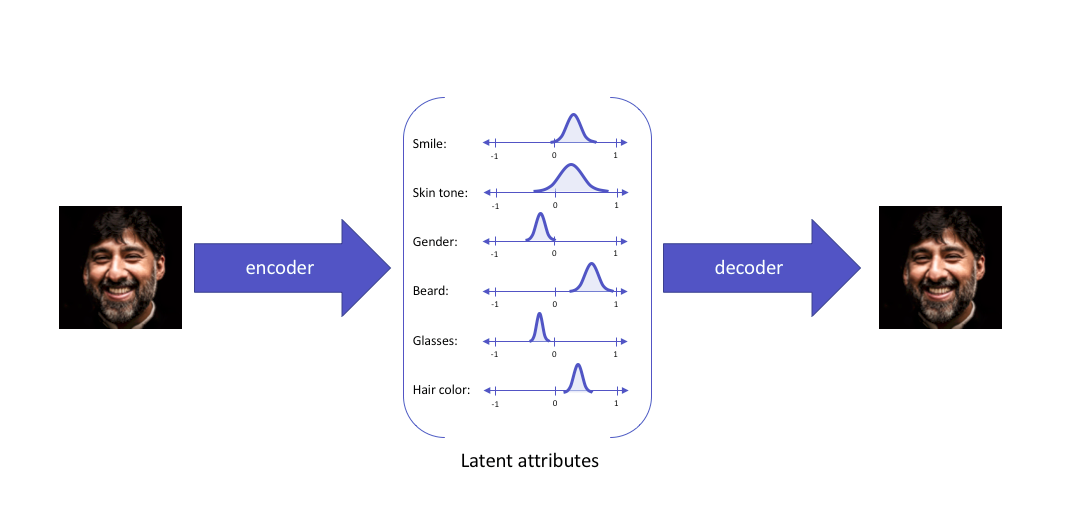
• Tuy nhiên, việc mã hóa nó dưới dạng một phân phối vẫn chưa đủ để đám bảo 2 yếu tố đã nếu ở đầu. Nó có thể sẽ đưa về một phân phối với tiny variances, hoặc một phân phối có sự sai khác mean lớn (các cụm cách xa nhau trong không gian tiềm ẩn). Đó là lý do, không những đưa về phân phối, ta còn phải chuẩn hóa phân phối, bao gồm chuẩn hóa covariance matrix và mean của phân phối.

• Hầu hết, việc chuẩn hóa sẽ cố gắng đưa về phân phối chuẩn. Mục tiêu cuối cùng là ngăn các phân phối đã mã hóa cách xa nhau trong không gian tiềm ẩn và khuyến khích càng nhiều càng tốt các phân phối trả về "chồng chéo nhau", nhờ đó, đạt được các điều kiện về tính liên tục và đầy đủ.

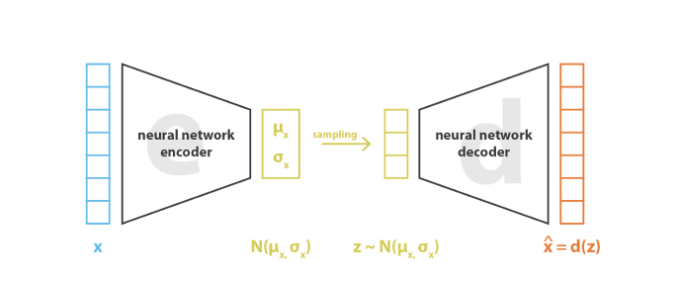
• Như vậy, ta thu được vecto $z$ được sample từ phân phối chuẩn có tuân theo trung bình $\mu$ và độ lệch chuẩn $sigma$. Từ đó, z được decode.

Triển khai code:

class VAE(torch.nn.Module):
   def __init__(self, latent_dim=20):
       super(VAE, self).__init__()
       self.encoder = Encoder(latent_dim)
       self.decoder = Decoder(latent_dim)

   def forward(self,inputs):
     z_mean, z_log_var = self.encoder(inputs)
     z = self.reparameterize(z_mean, z_log_var)
     reconstructed = self.decoder(z)
     return reconstructed, z_mean, z_log_var

   def reparameterize(self, mu, log_var):
     std = torch.exp(0.5 * log_var)
     eps = torch.randn_like(std)
     return mu + (eps * std)

Hàm mất mát

Ở phần AE đã sử dụng một hàm mất mát là reconstruction loss để đo lượng thông tin bị mất mát sau khi tái tạo. Đối với VAE cần phải có một hàm nữa để quản lý tính regular (đều đặn) của không gian tiềm ẩn, được gọi là regularisation loss. Hàm loss này được biểu thị dưới dạng Kulback-Leibler divergence (KL phân kỳ).

Đây là một phép đo sự khác nhau giữa một phân phối xác suất và đạt giá trị bằng 0 khi hai phân phối được coi là giống nhau. Hàm loss này sẽ cố gắng giảm thiểu sự phân kỳ KL giữa phân phối ban đầu và phân phối được tham số hóa của chúng tôi.

$$\text { loss }=\|x-x \hat{x}\|^{2}+\mathrm{KL}\left[N\left(\mu_{x}, \sigma_{x}\right), N(0, I)\right]$$

$$\text {loss} =\|x-d(z)\|^{2}+K L\left[N\left(\mu_{x}, \sigma_{x}\right), N(0, I)\right]$$

KL divergence loss ngăn cản mạng học các phân phối hẹp và cố gắng đưa phân phối gần hơn với phân phối chuẩn đơn vị.

$$\mathbf{K L}\left(N \left (\mu_x,\sigma_x\right), N\left(0, I_{d}\right)\right)=\frac{1}{2} \sum_{i=1}^{d}\left(\sigma\left(x\right)-\log \sigma \left(x\right)-1+\mu \left(x\right)^{2}\right)$$

def final_loss(reconstruction, train_x, mu, logvar):
   BCE = torch.nn.BCEWithLogitsLoss(reduction='sum')(reconstruction, train_x)
   KLD = -0.5 * torch.sum(1 + logvar - mu.pow(2) - logvar.exp())
   return BCE + KLD

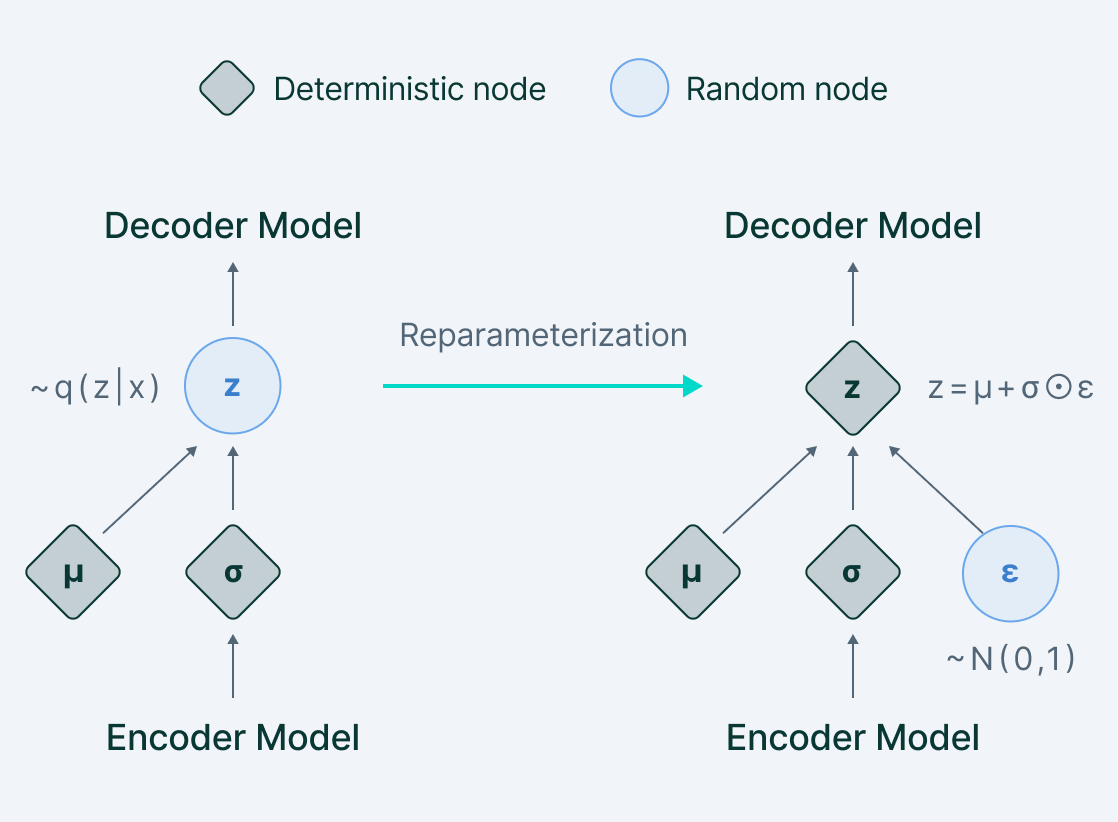
Reparameter trick

Ở phần triển khai code phía trên, có một phần được gọi là reparamater. Thông thường, để huấn luyện mạng neural network ta dùng thuật toán gradient descent, mà muốn thực hiện gradient descent thì phải có đạo hàm. Trong Variational Autoencoder, thì ta có một bước sample từ phân phối chuẩn để thu được vector ẩn $z$ để đưa qua decoder. Ơ, vậy chỗ sampling này thì lan truyền ngược thế nào.

Thay vì trực tiếp sample từ phân phối xác suất, người ta sử dụng 1 mẹo nhỏ gọi là reparameterization. Vector $z$ sẽ được tính bằng công thức.

$$z = \mu_x + \epsilon \odot \sqrt{\sigma_x}$$

trong đó $\epsilon \sim N(0, I_d)$.

Tại sao lại có công thức này?

Điều này đến từ thực tế rằng nếu $z$ là một biến ngẫu nhiên tuần theo phân phối Guassian với giá trị trung bình $\mu_x$ và hiệp phương sai $\sigma^2$ thì nó có thể biểu diễn ở dạng trên. Và đồng thời đó cũng là lý do ta có công thức hàm loss phía trên.

$$\mathbf{K L}\left(N \left (\mu_x,\sigma_x\right), N\left(0, I_{d}\right)\right)=\frac{1}{2} \sum_{i=1}^{d}\left(\sigma\left(x\right)-\log \sigma \left(x\right)-1+\mu \left(x\right)^{2}\right)$$

def reparameterize(self, mu, log_var):
     std = torch.exp(0.5 * log_var)
     eps = torch.randn_like(std)
     return mu + (eps * std)

4. Triển khai code

Đã đến đây rồi thì cùng lướt qua một tutorial rất đầy đủ mình lượm được trên AI Summer =)))) Mình cũng khá thích trang này, tuy không có quá nhiều bài viết những mỗi bài đều khá chỉn chu.

• AI Summer - JAX vs Tensorflow vs Pytorch: Building a Variational Autoencoder (VAE)

5. Autoencoding Variational Autoencoders (AVAE)

• The Autoencoding Variational Autoencoder

6. Kết - Tài liệu

Mặc dù thoạt nhìn, autoencoders có vẻ dễ dàng (vì chúng có nền tảng lý thuyết rất đơn giản), nhưng việc khiến chúng học cách biểu diễn đầu vào có ý nghĩa là điều khá khó khăn.

Cảm ơn tác giả bài viết gốc tiếng anh, một bài viết rất chi tiêt. Bài viết trên của mình vẫn còn nhiều chi tiết chưa truyền tải được (chắc chỉ được tầm 60%), bạn có thể xem bài viết gốc tại đây, nhất là phần Mathematical details of VAEs và lý do của cái tên Variational :

• Understanding Variational Autoencoders (VAEs)

• hoặc paper gốc: An Introduction to Variational Autoencoders

Thêm một bài viết nữa tổng quan chung về Autoencoder:

• An Introduction to Autoencoders: Everything You Need to Know (một senpai trong team có dịch một phần bài viết này, các bạn có thể đọc tại đây, phần Phân loại các dạng Autoencoder đặc biệt là VAE và DAE chưa đươc dịch, khá hay và có thể đọc thêm nếu muốn)

• https://machinelearningcoban.com/2017/03/04/overfitting

• Một senpai trong team cũng đã viết một bài giới thiệu tổng quan về VAE dành cho những ai nắm bắt nhanh và có kèm triển khai code, bạn có thể đọc tại đây: Giới thiệu vầ Variational Autoencoder

Bài viết đã dài. Mong mọi người thông cảm vì nó có phần hơi lan man và tản mạn. Nếu thấy bài hữu ích có thể tặng mình một Upvote cho mk có thêm động lực khai bút đầu xuân :vv.

Đồng thời bài viết này là để chuẩn bị cho một số bài viết khác sắp tới, hi vọng sẽ có ích.

Chúc mọi người năm mới vui vẻ thành công. 🥰