Introduction

Việc học một ngôn ngữ lập trình mới luôn thú vị nhưng cũng đầy thử thách. Với mình, một việc vô cùng quan trọng khi bắt đầu học một ngôn ngữ đó chính là tìm tài liệu đủ tốt để có thể giúp mình hiểu sâu về bản chất cũng như những tính năng, đặc điểm mà ngôn ngữ đó mang lại. Với C, chúng ta không thể bỏ qua "The C Programming Language", do chính tác giả của C viết, tương tự như vậy, với Swift, chắc chắn quyển sách đầu tiên các bạn nên đọc là "The Swift Programming Language" được phát hành bởi Apple. Tuy nhiên, để có thể sử dụng một ngôn ngữ lập trình một cách thành thạo và hiệu quả, bên cạnh việc đọc tài liệu tốt, chúng ta cần phải thực hành với nó thật nhiều. Có rất rất nhiều cách để bạn có thể thực hành với một ngôn ngữ: làm một ứng dụng nho nhỏ, nhái lại những đoạn code của các cao thủ,...Với mình cách hiệu quả nhất chính là áp dụng những kiến thức về khoa học máy tính, giải thuật, hay design pattern mà mình đã được học và được thực hành ở các ngôn ngữ khác vào ngôn ngữ mình muốn học.

Bài viết này mình không nhằm giới thiệu về Swift, mà mình muốn sử dụng Swift để giải quyết các vấn đề, các bài toán rất phổ thông trong quá trình các bạn tiếp cận với lập trình, vì thế, nó khá hợp cho những bạn nào muốn tìm hiểu cơ bản về khoa học máy tính, về giải thuật hay đơn giản là tò mò về cách mà chúng ta sử dụng máy tính để giải quyết các vấn đề.

Lưu ý rằng bài viết này không phải dành cho những bạn chưa biết gì về Swift, bạn cần phải có chút kiến thức cơ bản về ngôn ngữ này, không cần quá sâu, chỉ cần đi hết chuơng này là được (https://docs.swift.org/swift-book/LanguageGuide/TheBasics.html), nếu bạn chưa lập trình bao giờ, hãy đọc qua những khái niệm cơ bản như biến, hàm,... trước khi bắt đầu

Do KHMT là một lĩnh vực rất rộng, nên thật khó để mình có thể trình bày mọi thứ được mà sẽ chỉ đề cập đến những vấn đề thường gặp nhất, phổ thông nhất mà mình được giới thiệu ở trường đại học. Những vấn đề này mình sắp xếp theo thứ tự phức tạp tăng dần, từ những vấn đề mà chỉ vài dòng code, 1 hàm nhỏ là có thể giải quyết, gói gọn trong 1 bài, cho đến những vấn đề phức tạp mà có lẽ phải vài bài, phải xây dựng cả một hệ thống mới xong. Ở mỗi bài viết mình đều đặt categories cho vấn đề mình sẽ để cập để các bạn có thể dễ theo dõi

Còn 1 điều cuối: nhiều bạn lo ngại rằng nếu không có macos sẽ không lập trình Swift được, mình ban đầu cũng tưởng như vậy, nhưng thực sự là bây giờ có quá nhiều phuơng pháp để các bạn có thể thực hành với ngôn ngữ này:

• Nếu các bạn đang có macOS: quá tốt rồi, chỉ cần cài thêm Xcode và mở playground lên là xong
• Nếu các bạn đang dùng Windows: Google từ khóa: "online swift playground" và chọn 1 trang giúp bạn thoải mái nhất
• Nếu các bạn dùng Linux: có thể theo cách trên, hoặc các bạn có thể cài đặt Swift trên máy theo hướng dẫn sau: (https://www.digitalocean.com/community/tutorials/how-to-install-swift-and-vapor-on-ubuntu-16-04) - không cần cài Vapor nhé

Small Problems

The Fibonacci Sequence (dãy số Fibonacci)

Một trong những bài toán mà mình tin rằng bất cứ lớp học nào về giải thuật đều sẽ đề cập là bài toán về dãy số Fibonacci, bài toán thường được cho dưới đề bài như sau:

Hãy tìm số fibonacci thứ n

Rất ngắn gọn phải không nào? OK chúng ta bắt đầu phân tích vấn đề

1. Dãy fibonacci là gì? Nếu bạn chưa biết hoặc quên, thì dãy số Fibonacci là dãy số mà trong đó, trừ 2 số đầu tiên, số tiếp theo của dãy bằng tổng 2 số liền trước nó, ví dụ

0, 1, 1, 2, 3, 5, 8, 13, 21...

Như vậy, ta có thể xây dựng một công thức tổng quát cho số fibonacci thứ n:

fib(n) = fib(n - 1) + fib(n - 2)

2. Hướng tiếp cận đệ quy Đây thường là hướng mà các thầy ở trường đại học sẽ sử dụng (trên thực tế, đây là một trong những bài toán kinh điển nhất mà luôn luôn được giới thiệu khi bạn được dạy về đệ quy) Cho những bạn nào chưa rõ: trong KHMT, một hàm được gọi là đệ quy khi nó gọi lại chính nó, cụ thể ra sao thì mời xem tiếp phần code bên dưới

func fib1(n: UInt) -> UInt {
    return fib1(n: n - 1) + fib1(n: n - 2)
}

Như các bạn thấy, ở đây ta định nghĩa hàm fib1(), và trong thân hàm fib1(), ta lại gọi lại nó, đây chính là đặc điểm dễ nhận biết nhất của một hàm đệ quy

Tại sao mình lại chọn các tham số đầu vào và kết quả trả về là UInt mà không phải là Int? rất đơn giản, vì các phần tử trong dãy Fibonacci là các số nguyên duơng

Nếu bạn chạy thử hàm trên với một số nguyên duơng bất kì, thì thật bất ngờ, chuơng trình có vẻ như đang chạy tuy nhiên lại chẳng có kết quả gì trả về cả? vì sao vậy?

Câu trả lời là bạn đang rơi vào vòng lặp vô tận, hãy cùng phân tích sâu hơn vấn đề. Tạm gạt bài toán này sang một bên, hãy xem xét lại vấn đề về đệ quy, bạn hiểu đệ quy như thế nào? có thể đưa ra ví dụ được không?

Một trong những ví dụ đơn giản nhất đối với mình là bài toán điểm danh: tưởng tượng bạn xếp một hàng rất dài theo chiều dọc, làm sao để người đầu hàng có thể biết được hàng của mình có bao nhiêu người? Một cách tự nhiên, không biết thì phải hỏi, anh ta sẽ hỏi người đứng liền sau mình xem phía sau anh ta có bao nhiêu người

Rất tiếc là người đứng sau đó (tạm gọi là người thứ 2) cũng không biết, anh ta lại quay xuống hỏi người thứ 3, cứ tiếp tục như vậy cho tới người cuối hàng. Người cuối hàng (gọi là người thứ n) quay xuống và không thấy ai, anh ta sẽ trả lời cho người phía trên mình (n-1), từ đó người (n-1) có thể biết ra được đằng sau mình có bao nhiêu người và câu trả lời được đẩy dần lên trên cho người đầu hàng

Nhưng nếu bạn đứng ở một hàng dài vô tận thì sao?, điều đó có nghĩa không có ai là người cuối cùng, đồng nghĩa người đầu hàng sẽ không bao giờ nhận được câu trả lời!

Quay trở lại với ví dụ trên, ta nhận thấy, nếu cứ gọi lại hàm fib1() với các tham số là n-1 rồi n-2, rồi chúng lại tiếp tục gọi như thế ở lần lặp tiếp theo, cứ trừ mãi trừ mãi như vậy thì việc gọi hàm sẽ diễn ra vô tận, và chuơng trình của bạn đơn giản là sẽ không bao giờ trả về kết quả cho bạn.

Vậy tóm lại, vấn đề ở đây là gì? đó là ta đang thiếu một điểm dừng, gọi phải đến một lúc nào đó, đến một tham số nào đó phải dừng lại, chứ không thể gọi mãi gọi mãi như vậy, lặp thì phải có điều kiện dừng, đúng không?

Trong đệ quy, ở một điều kiện nào đó khiến cho việc gọi đệ quy dừng lại gọi là một điểm neo. Vậy điểm neo đối với bài toán Fibonacci này là gì?

Lại quay trở lại với định nghĩa ban đầu: ta luôn phải có sẵn 2 số đầu (0 và 1) thì mới có thể tiến hành tính toán được giá trị tiếp theo, vậy hàm fib1() có thể cải tiến thêm 1 chút như sau:

func fib2(n: UInt) -> UInt {
    if (n < 2) {
        return n
    }
    return fib2(n: n - 2) + fib2(n: n - 1) 
}

giải thích qua một chút: nếu phải tìm số fibonnaci thứ 0 và 1, thì ta không tiến hành đệ quy mà chỉ đơn giản trả về nó thôi (chú ý rằng chúng ta đếm từ 0 nhé, không phải từ 1 đâu )

Nếu bạn thực hiện gọi hàm này như sau, kết quả sẽ vô cùng mĩ mãn, bài toán có vẻ như đã được giải quyết:D

fib2(n: 5)
fib2(n: 10)

Nhưng thử gọi hàm này như sau:

fib2(n: 50)

Chuơng trình của bạn sẽ lại treo và không đưa ra kết quả gì. Lại rơi vào vòng lặp vô tận sao? Hoàn toàn không phải như vậy vì ta đã có điểm neo rồi, hãy thử phân tích xem chuơng trình của chúng ta thực sự hoạt động như thế nào

Quan sát thân hàm fib2(), ta có thể thấy với mỗi lời gọi fib2() sẽ sinh ra 2 lời gọi khác, như vậy bạn có thể dễ thấy rằng số lời gọi sẽ tăng lên rất nhanh theo hàm mũ

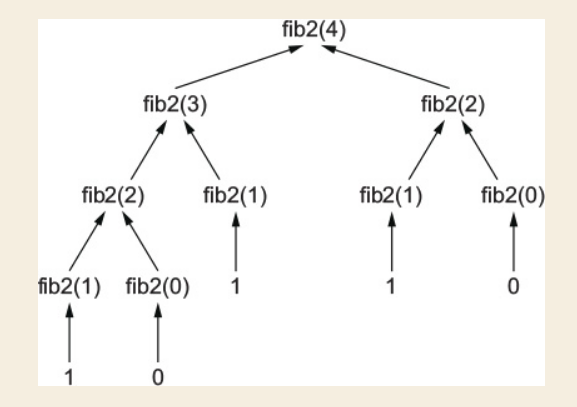
với n = 4, số lời gọi đã là 9, với n = 20, số lời gọi đã là 21,891 rồi! Vậy có giải pháp nào tốt hơn cho trường hợp này không?

Hãy cùng xem lại đồ thị lời gọi trên, bạn nhận ra điều gì "sai sai" ở đây chứ?

Nếu bạn chưa nhận ra, thì đó là chúng ta đang gọi đi gọi lại quá nhiều 1 hàm với tham số giống nhau! tại sao ở đây chúng ta gọi fib2(2) quá nhiều lần (và cũng chỉ trả ra 1 kết quả như nhau) vậy? Đó chính là vấn đề. Nếu tôi tính và ra kết quả rồi, tại sao tôi lại phải tính lại? sẽ tốt hơn nếu tôi tính rồi, lưu lại kết quả ở đâu đó, và khi cần tôi chỉ cần gọi lại kết quả đó ra mà không cần tính lại nữa

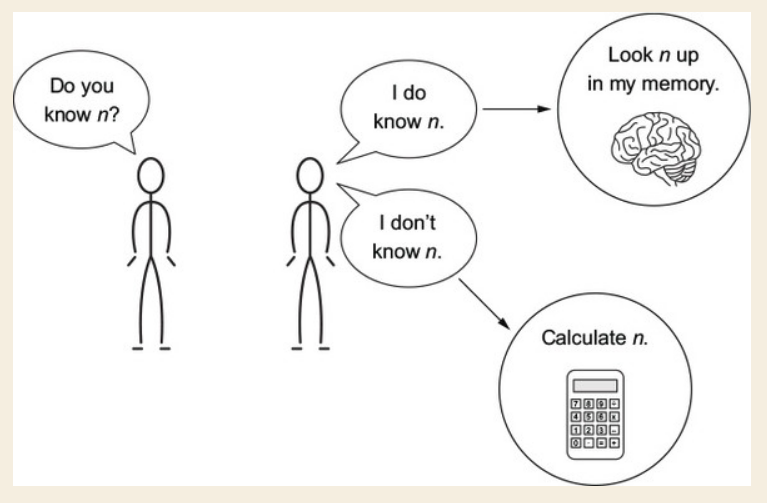
Kĩ thuật này được gọi là "đệ quy có nhớ"

Với tư tưởng đó, ta có thể cái tiến thuật toán như sau:

var fibMemo: [UInt: UInt] = [0: 0, 1: 1]
func fib3(n: UInt) -> UInt {
    if let result = fibMemo[n] { 
        return result
    } else {
        fibMemo[n] = fib3(n: n - 1) + fib3(n: n - 2)
    }
    return fibMemo[n]!
}

chạy thử với fib3(50), kết quả ra ngay tức khắc

ở đây mình nói riêng về Swift một chút, như bạn thấy, mình đã unwrap biến ở return, thường thì chúng ta rất nên tránh sử dụng unwrap thì nó dẫn đến crash chưong trình, tuy nhiên ở đây do mình biết 100% nó không thể nil nên có thể dùng

Vấn đề tới đây đã được giải quyết? Có thể, nếu bạn đã thỏa mãn với kết quả (đã rất tốt) này. Nếu bạn không vội, thì mình xin kể một câu chuyện khá thú vị khi mình được thầy giáo giới thiệu bài toán này, khi đó mình chưa biết gì về đệ quy, và đưa ra một cách giải không đệ quy như sau (hồi đó mình viết bằng C, nhưng ở đây diễn lại với Swift nhé)

func fib4(n: UInt) -> UInt {
    if (n == 0) { 
        return n
    }
    var last: UInt = 0, next: UInt = 1 
    for _ in 1..<n {
        (last, next) = (next, last + next)
    }
    return next
}

Như bạn có thể thấy, đây là một cách giải rất tự nhiên dựa trên những định nghĩa cơ bản về dãy Fibonacci đúng không? không có gì khó hiểu như đệ quy gì hết!

Thật tình cờ đây lại là một cách giải rất tốt, cho kết quả chạy rất nhanh. Bạn có thể dễ dàng thấy với n = 20, vòng lặp của mình cũng chỉ chạy tối đa 19 lần (so với phưong pháp giải đệ quy là hơn 21000 lần!)

Điều đó cho thấy rằng đệ quy không phải bao giờ cũng là tốt nhất (trên thực tế thì nó khá tệ ở đa số trường hợp), nếu sử dụng đệ quy một cách không khéo léo, bạn sẽ rất dễ gặp vấn đề về hiệu năng của chuơng trình.

Hơn nữa, những bài toán đệ quy luôn luôn có thể giải được với phưong pháp không đệ quy

Conclusion

Woa, không ngờ là mình có thể viết 1 bài dài đến vậy . Mong rằng qua bài này, các bạn có thể hiểu được cơ bản về đệ quy (đệ quy còn rất nhiều bài toán khác), nhưng điều quan trọng hơn, chúng ta đã bước đầu hình thành được cách suy nghĩ phân tích và giải quyết vấn đề và sử dụng ngôn ngữ Swift để giải quyết vấn đề đó. Ở bài tới, mình sẽ trình bày một bài toán cũng về đệ quy và không kém phần nổi tiếng so với bài toán Fibonacci, đó là bài toán Tháp Hà Nội, bài toán đã khiến mình mãi mới có thể hiểu được khi mới học Hẹn gặp lại các bạn ở bài viết đó nhé!