Giới thiệu

Năm 2020, DDPM (Denoising Diffusion Probabilistic Models) đưa ra một số cải tiến, đơn giản hoá cho mô hình diffusion và đạt được SOTA trên tập CIFAR10. Vài tháng sau đó, đầu năm 2021, OpenAI xuất bản một paper đưa ra một số cải tiến cho DDPM. Trong bài viết này mình sẽ cố gắng làm nổi bật một số điều hay ho trong paper cải tiến này. Mặc dù rất nhiều settings trong DDPM vẫn còn được dùng trong những SOTA đến tận bây giờ, nhưng những settings trong paper cải tiến sẽ cũng cung cấp cho chúng ta thêm một option để thử cải thiện mô hình của mình tuỳ vào từng bài toán cụ thể.

Paper sẽ tập trung cải thiện hai phần metric là log-likelihood và tốc độ sample vốn là điểm yếu cố hữu của mô hình diffusion.

Mình sẽ không nhắc lại background về mô hình diffusion trong bài viết này, để nhớ lại các kiến thức background các bạn có thể tham khảo bài viết từ phần II. Sau đây chúng ta sẽ đi vào các phần chính của paper.

Cải thiện Log-likelihood

Mặc dù có chất lượng các sample tốt tuy nhiên DDPM có một nhược điểm là log likelihood của nó không tốt bằng các phương pháp likelihood-based khác. Chính tác giả của DDPM đã thừa nhận điều này. Log-likelihood là một metric được sử dụng rộng rãi để đánh giá mô hình sinh. Người ta tin rằng việc tối ưu log-likelihood sẽ ép mô hình sinh bắt được tất cả các mode của phân phối dữ liệu. Một cải thiện nhỏ của log-likelihood có thể ảnh hưởng lớn đến chất lượng sample và biểu diễn đặc trưng học được. Đó là lý do tại sao tác giả nhắm đến cải thiện metric này. Và trong paper cải tiến, tác giả đã cho thấy bằng một vài thay đổi, mô hình diffusion hoàn toàn có thể đạt được log-likelihood ngang với các mô hình likelihood-based khác.

Xem xét lại việc học $\Sigma_\theta(x_t, t)$

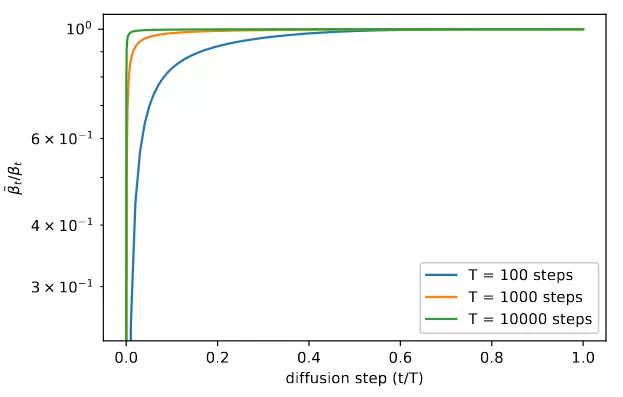
Trong paper DDPM, tác giả đặt $\Sigma_\theta(x_t, t) = \sigma^2_tI$, với $\sigma_t$ cố định. Giá trị của $\sigma_t$ có thể chọn miễn là thoả mãn $\tilde{\beta_t} \leq \sigma^2_t \leq \beta_t$. Tuy nhiên, một điều khá thú vị là dù chọn $\sigma^2_t$ là $\tilde{\beta_t}$ hay $\beta_t$ thì chất lượng sample thu được không thay đổi đáng kể. Hình 1 phía dưới đây lý giải phần nào nguyên nhân của điều này. Ta thấy $\tilde{\beta_t}$ và $\beta_t$ gần như bằng nhau ở hầu hết các timestep chỉ trừ vùng gần t=0. Và thậm chí nếu tăng T thì hai giá trị này còn gần với nhau hơn. Vì ở các khoảng thời gian t=0, mô hình sẽ xử lý những chi tiết khó có thể nhận biết được bằng mắt thường nên lựa chọn $\sigma$ khác nhau cũng ít ảnh hưởng đến chất lượng sample, điều này còn đúng hơn nếu ta tăng T.

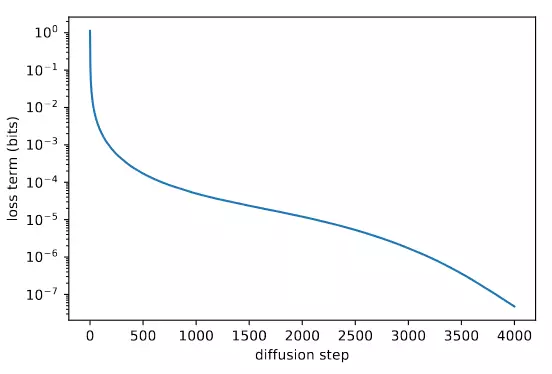
Đó là về chất lượng của sample, còn về log-likelihood thì từ hình 2 ta có thể thấy rằng, các bước gần t=0 lại đóng góp nhiều vào variational lower bound nhất. Như vậy trong khi thay đổi $\Sigma_\theta(x_t, t)$ không ảnh hưởng tới chất lượng sample, nó lại có thể cải thiện log-likelihood. Do đó, chúng ta cần phần học $\Sigma_\theta(x_t, t)$.

Có một vấn đề với việc học $\Sigma_\theta(x_t, t)$ là khoảng giá trị của nó rất nhỏ, thậm chí trên log scale, điều này khiến cho mô hình rất khó có thể dự đoán. Do đó, thay vì trực tiếp dự đoán $\Sigma_\theta(x_t, t)$, tác giả tham số hoá nó dưới dạng nội suy giữa $\tilde{\beta_t}$ và $\beta_t$ như sau:

$$\Sigma_\theta(x_t, t) = \exp(v \log(\beta_t) + (1-v)\log\tilde{\beta_t})$$

Với việc tham số hoá như trên thì mô hình chỉ cần dự đoán giá trị của vector $v$. Tuy nhiên, có một vấn đề khác là hàm loss trong DDPM đã được giản lược và không phụ thuộc vào $\Sigma_\theta(x_t, t)$ nên ta cần 1 hàm loss mới:

$$L_{hybrid} = L_{simple} + \lambda L_{vlb}$$

Để tránh $L_{vlb}$ lấn át $L_{simple}$, Tác giả set $\lambda = 0.001$ và áp dụng stop-gradient với $\mu_\theta (x_t, t)$ cho $L_{vlb}$.

Cải thiện noise schedule

Linear noise schedule được sử dụng trong DDPM hoạt động tốt với ảnh phân giải cao tuy nhiên không tối ưu trên những ảnh có kích thước 64x64 và 32x32. Tác giả cho rằng ở cuối quá trình diffusion thuận quá nhiễu, do đó nó không đóng góp nhiều vào chất lượng của sample. Điều này được minh hoạ ở hình 3.

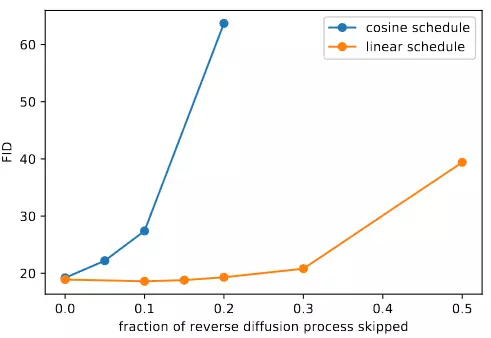
Tác giả thử bỏ đi 20% đầu của quá trình reverse thì thấy FID giảm không nhiều, xem kết quả ở hình 4. Để giải quyết vấn đề này, tác giả đề xuất cosine noise schedule khác dựa vào $\bar{\alpha_t}$:

$$\bar{\alpha_t} = \frac{f(t)}{f(0)} , f(t) = {\cos(\frac{t/T + s}{1 + s} \frac{\pi}{2})}^2$$

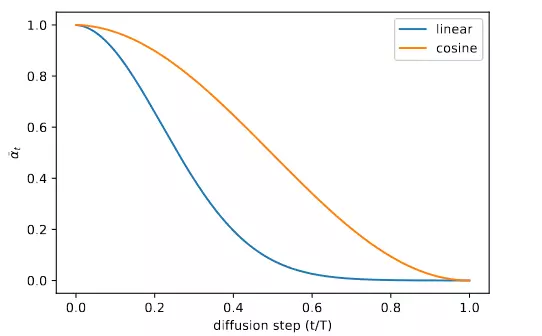
Cosine schedule được thiết kế để giảm tuyến tính theo $\bar{\alpha}_t$ ở giữa quá trình và thay đổi rất nhỏ ở gần $t = 0$ và $t = T$. Hình 5 cho thấy sự thay đổi của $\bar{\alpha_t}$ cho cả hai schedule. Chúng ta có thể thấy với linear schedule thì $\bar{\alpha}_t$ giảm khá nhanh, điều này cũng đồng nghĩa với việc phá huỷ thông tin khá nhanh (vì $x_t = \bar{\alpha}_t x_0+ (1 - \bar{\alpha}_t) \epsilon$)

Giảm gradient noise

Tác giả thấy rằng cả $L_{vlb}$ và $L_{hybrid}$ đều giao động rất mạnh. Để cải thiện điều này tác giả đã sử dụng importance sampling thay vì sampling t theo phân phối uniform:

$$L_{vlb} = E_{t \sim p_t} [\frac{L_t}{p_t}]$$

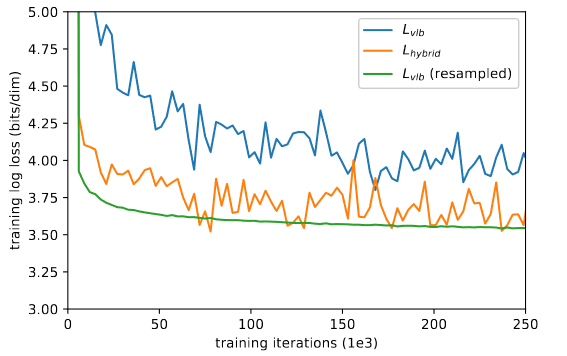
trong đó $p_t \propto \sqrt{E[L^2_t]}$ và $\Sigma p_t = 1$. Vì $E[L^2_t]$ thay đổi trong quá trình training nên chúng ta sẽ cần lưu lại lịch sử (tác giả sử dụng 10 lần gần nhất) của các thành phần này để xấp xỉ. Ban đầu ta sẽ chọn uniform 10 sample cho đến khi đủ 10 sample mỗi $t \in [0, T-1]$. Hình 6 thể hiện learning curve đã được cải thiện khi áp dụng importance sampling(resampled).

Cải thiện tốc độ sampling

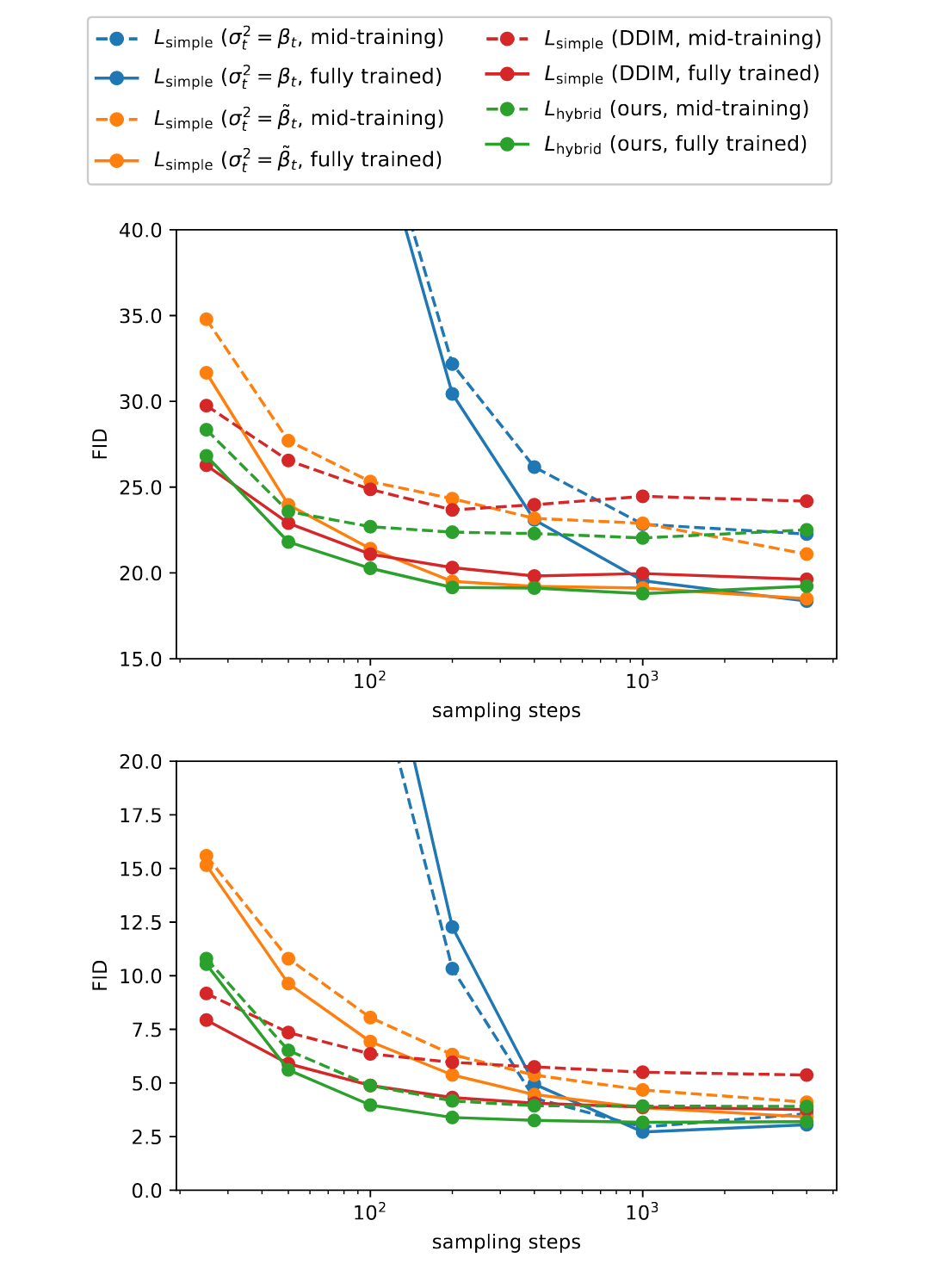
Việc chạy hàng nghìn bước reverse có thể tốn đến vài phút trên một GPU (kể cả RTX3090) chỉ để sinh ảnh độ phân giải cao. Điều này là cực kỳ tốn kém. Tác giả ngạc nhiên phát hiện ra rằng, những thay đổi trên nhằm cải thiện log-likelihood cũng làm cho chất lượng của sample tốt hơn khi sampling với ít step hơn. Kết quả được thể hiện ở Hình 7. Khi cố định $\sigma$(cả với giá trị lớn nhất hoặc nhỏ nhất)), chất lượng sample bị giảm nhanh chóng khi giảm số step sampling. Trong khi với mô hình học bằng $L_{hybrid}$, với số step khoảng 100 cho kết quả gần tối ưu (train với 4000 step). Các step được chọn để cách đều nhau giữa 1 đến T (làm tròn về số integer gần nhất). Trong hình 7, phương pháp cải tiến này cũng được đem ra so sánh với DDIM. DDIM là một phương pháp sampling khác cũng nhắm đến việc giảm thời gian sampling. Ta có thể thấy phương pháp cải tiến đang bàn đến kém hơn DDIM với số step nhỏ hơn 50, tuy nhiên với số step lớn 50 thì phương pháp cải tiến cho FID tốt hơn.

Kết bài

Trong các phần trên mình đã nêu các điểm chính trong paper cải tiến DDPM. Mình nghĩ đây là một trong những paper rất nên đọc để hiểu hơn về mô hình diffusion và ảnh hưởng của các thành phần của nó cho các bạn mới. Hy vọng bài viết này hữu ích với bạn, nếu đúng thế thì đừng quên cho mình 1 upvote nhé. Cảm ơn và hẹn gặp lại trong bài viết tiếp theo về mô hình diffusion.

Tài liệu tham khảo

Paper: Improved Denoising Diffusion Probabilistic Models