Duyệt đồ thị (Graph Traversal)

Phần II này sẽ tập trung thảo luận về 2 thuật toán đồ thị cơ bản: Tím kiếm theo chiều sâu (Depth-First Search) hay thường gọi là DFS và Tìm kiếm theo chiều rộng (Breadth-First Search) viết tắt là BFS (còn tên gọi khác là thuật toán Loang).

Cả 2 thuật toán này đều được cung cấp 1 nút bắt đầu trong đồ thị và chúng ta sẽ truy cập tất cả các nút có thể truy cập được từ nút bắt đầu. Sự khác biệt giữa 2 thuật toán này là thứ tự truy cập các nút của chúng.

Depth-First Search (DFS)

Thuật toán DFS (tìm kiếm theo chiều sâu) là một kỹ thuật duyệt đồ thị đơn giản. Thuật toán bắt đầu với 1 nút nguồn và tiến tới các nút khác có thể tiếp cận được từ nút nguồn bằng cách sử dụng các cạnh của đồ thị.

Tìm kiếm theo chiều sâu luôn theo một đường dẫn (path) duy nhất trong đồ thị miễn là nó tìm thấy các nút mới. Sau đó, nó quay lại các nút trước đó và bắt đầu khám phá các phần khác của đồ thị. Thuật toán này có đánh dấu lại các nút đã thăm, do đó nó chỉ đi qua mỗi nút một lần.

Tôi sẽ lấy ví dụ để chúng ta xem cách thức mà DFS hoạt động một cách trực quan hơn với đồ thị dưới đây:

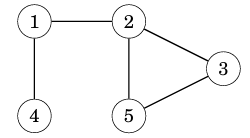
Chúng ta sẽ duyệt toàn bộ các nút của đồ thị trên với DFS. Ta có thể chọn nút nguồn là bất kì nút nào của đồ thị; Tại đây tôi sẽ chọn tạm nút 1 là nút nguồn. Đầu tiên ta di chuyển đến nút 2 thông qua cạnh (như vậy ta đã thăm được nút 2)

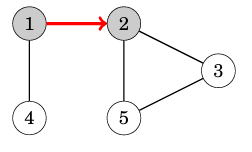
Sau đó, ta tiếp tục thăm nút 3 và nút 5 theo đường dẫn mà ở phần lý thuyết bên trên ta đã nhắc.

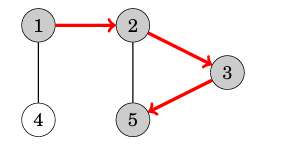
Ta có thể thấy hàng xóm của nút 5 hay nút kề với nút 5 là 2 và 3, nhưng trong quá trình duyệt vừa rồi ta đã thăm cả 2 nút này rồi nên đã đến lúc quay lại các nút trước đó. Ta quay lại nút 2 và nút 3 thì đều thấy các hàng xóm (hay nút kề) của các nút này đều đã được thăm nên ta quay lại nút 1 và tiến hành thăm nốt nút 4 là hàng xóm của nút 1.

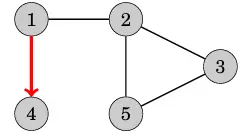
Như vậy là ta đã truy cập tất cả các nút của đồ thị.

Độ phức tạp thời gian của DFS là O(n + m) trong đó n là số nút và m là số cạnh, vì thuật toán xử lý với mỗi nút và mỗi cạnh chỉ 1 lần.

Tiếp theo là phần Implement Code của DFS với C++:

DFS có thể được triển khai thuật tiện bằng cách sử dụng đệ quy hoặc stack. Tùy mỗi người, hầu như thấy đệ quy dùng tiện hơn nhưng mình lại quen code với stack.

Đầu tiên ta sử dụng danh sách kề để lưu trữ đồ thị

vector<int> graph(n);

và sử dụng một vector<bool> vis để đánh dẫu các nút đã thăm.

vector<bool> visited(n, false)

Ban đầu, mỗi giá trị của visited được đánh dấu là false và khi duyệt đến nút s chẳng hạn thì ta gán visited[s] = true. Điều này tránh việc ta thăm 1 nút 2 lần.

Với việc triển khai DFS bằng đệ quy, ta triển khai như sau:

void dfs(int s) {
    if(visited[s]) return;
    visited[s] = true;
    // process node s
    for(auto u : graph[s]) {
        dfs(u);
    }
}

Với cách triển khai bằng Stack

void dfs(int s) {
    stack<int> st;
    st.push(s);
    vis[s] = true;
    while(!st.empty()) {
        auto cur = st.top();
        st.pop();
        for(auto u : graph[cur]) {
            if(!vis[u]) {
                st.push(u);
                vis[u] = true;
            }
        }
    }
}

Với dạng lưu trữ đồ thị ở dạng ma trận như ta đã nói ở P1. Thì ta triển khai theo cả 2 cách như sau:

vector<vector<int>> grid(r, vector<int> c);

Vector 2 chiều để lưu trữ đồ thị với r hàng, c cột.

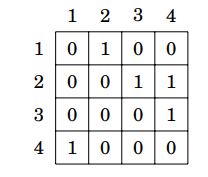
Tôi xin nhắc lại 1 chút: với ma trận ta có thể di chuyển theo 4 hướng: lên trên, xuống dưới, sang trái, sang phải. Với 1 là đường có thể đi, 0 là vật cản hay nước không thể đi.

vector<vector<bool>> vis;

Tương tự như trên ta cũng sử dụng vis để đánh dấu tọa độ các nút đã thăm.

vector<pair<int, int>> directions = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};

Cái này dùng để di chuyển theo 4 hướng lên trên, xuống dưới, sang trái, sang phải

Với cách sử dụng đệ quy:

void dfs(pair<int, int> s, vector<vector<int>>& grid, vector<vector<bool>>& vis) {
    int x = s.first;
    int y = s.second;
    
    if (x < 0 || x >= grid.size() || y < 0 || y >= grid[0].size() || vis[x][y] || grid[x][y] != 1) {
        return;
    }
    
    vis[x][y] = true;
    
    vector<pair<int, int>> directions = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
    
    for (const auto& dir : directions) {
        int newX = x + dir.first;
        int newY = y + dir.second;
        dfs(make_pair(newX, newY), grid, vis);
    }
}

Với cách sử dụng stack

void dfs(pair<int, int> start, vector<vector<int>>& grid, vector<vector<bool>>& vis) {
    vector<pair<int, int>> directions = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
    stack<pair<int, int>> s;
    s.push(start);
    
    while (!s.empty()) {
        pair<int, int> current = s.top();
        s.pop();
        
        int x = current.first;
        int y = current.second;
        
        if (x < 0 || x >= grid.size() || y < 0 || y >= grid[0].size() || vis[x][y] || grid[x][y] != 1) {
            continue;
        }
        
        vis[x][y] = true;

        for (const auto& dir : directions) {
            int newX = x + dir.first;
            int newY = y + dir.second;
            s.push(make_pair(newX, newY));
        }
    }
}

Mai viết nốt BFS HAHA