Imagen - Mô hình SOTA giải quyết bài toán Text-to-Image

Imagen - mô hình mới được công bố gần đây bởi Google với khả năng generate hình ảnh từ đoạn text mô tả bất kỳ, cho dù ảnh đó không có thật hoặc phi logic. Phía trên là một ví dụ của ảnh được sinh ra bởi mô hình, rất ấn tượng phải không ?

Bạn cũng có thể đọc bài viết tại đây: http://bit.ly/3xuknLS

1. Tổng quan về các mô hình Generative

4 họ model nổi bật trong tác vụ Generation:

GAN: Huấn luyện dựa vào cơ chế học đối kháng với 2 thành phần: bộ sinh ảnh và bộ phân loại
VAE: Tìm cách học một mô hình có khả năng biểu diễn phân phối của training data, sau đó sample biến ẩn từ phân phối học được và đưa qua decoder để sinh ảnh
Flow-based model: Sử dụng một chuỗi các phép biến đổi khả nghịch (invertible transform) và sử dụng negative log-likelihood loss nhằm học phân phối dữ liệu một cách tường minh.
Diffusion Model: Từ từ phá hủy cấu trúc của ảnh bằng cách thêm dần nhiễu, mô hình được huấn luyện để học cách phục hồi nhiễu về ảnh ban đầu.

Nhờ sử dụng Diffusion Model làm cốt lõi và tận dụng sức mạnh của mô hình pretrained language lớn, đội ngũ của Google Research Team đã phát triển và tạo ra Imagen với khả năng Generation ảnh hết sức mạnh mẽ. Nào, cùng tìm hiểu sâu hơn một chút về Diffusion model và điều gì đã khiến nó trở nên rất "hot" trong thời gian gần đây thôi. Let's go !

2. Diffusion Model - a new approach for Generation Task

2.1 Ý tưởng chung

Xuất phát từ paper năm 2015 bởi các sinh viên đại học Stanford, mô hình được lấy cảm hứng từ nguyên lý khuếch tán trong lĩnh vực nhiệt động lực học, các bạn có thể đọc thêm về paper tại đây. Ý tưởng chung là phá hủy một phân phối dữ liệu một cách từ từ và có kiểm soát thông qua một chuỗi cách khuếch tán thuận, việc của chúng ta lúc này là tìm cách học một mô hình có thể đảo ngược quá trình khuếch tán đó nhờ đó có thể phục hồi lại cấu trúc dữ liệu ban đầu. Mô hình sau khi học được cách đảo ngược quá trình đó có thể được sử dụng cho tác vụ generation một cách hiệu quả.

Ảnh: Minh họa quá trình khuếch tán theo từng step

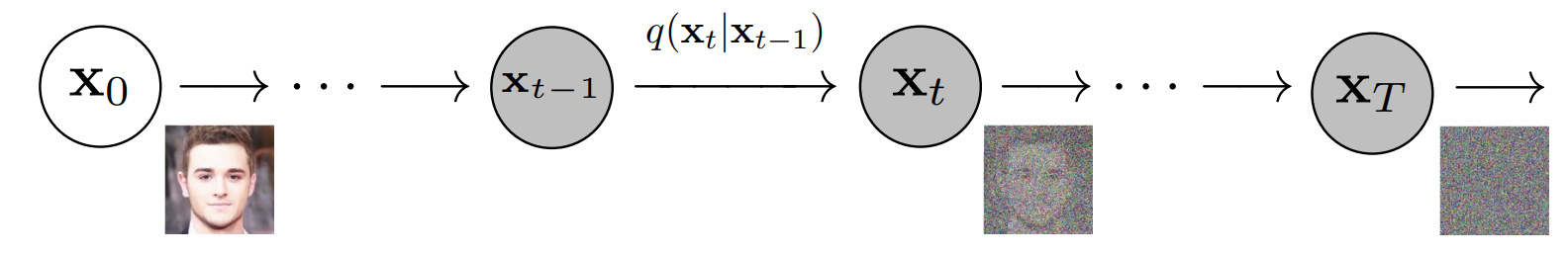
Cụ thể khi áp dụng với hình ảnh, quá trình khuếch tán thuận là một chuỗi các phép biến đổi bao gồm nhiều step, tại mỗi step ảnh nhiễu từ step trước lại được thêm Gaussion noise để gia tăng độ nhiễu, quá trình thêm nhiễu xảy ra dần dần và dừng lại khi ảnh hoàn toàn chỉ là nhiễu mà không còn đặc trưng thông tin ban đầu. Từ nhiễu thu được ở cuối quá trình thuận,chúng ta tìm cách khử nhiễu ảnh dần dần theo từng step để thu được ảnh gốc ban đầu.

Ảnh: Quá trình sinh ảnh từ trái sang phải bằng cách khử dần nhiễu

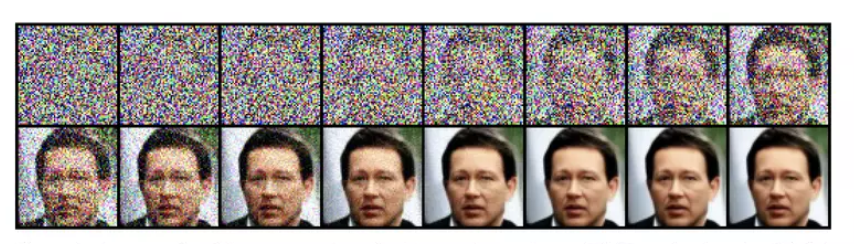
Câu hỏi đặt ra là tại sao chúng ta phải thực hiện thêm nhiễu và khử nhiễu thông qua một chuỗi rất nhiều các step ? Lý do khá đơn giản, thay vì trực tiếp giải bài toán khó chúng ta chia nhỏ vấn đề ra và giải quyết dần dần từng chút một, điều này giúp mô hình có thể "tiêu hóa" một cách dễ dàng. Vậy chúng ta khử nhiễu bằng cách nào ? Bằng cách huấn luyện một mô hình nhận đầu vào là ảnh nhiễu và predict ra một phần nhiễu của ảnh đó, ảnh bớt nhiễu có được bằng việc lấy ảnh nhiễu "trừ" đi nhiễu đã predict được. Khi phải học cách tái tạo lại một số lượng lớn các hình ảnh, mô hình sẽ "vô tình" nắm bắt được biểu diễn ẩn của phân phối dữ liệu được dùng từ đó sản sinh ra các hình ảnh tương tự.

Nền tảng toán học đằng sau diffusion model mình sẽ trình bày ở phần phụ lục cuối bài viết.

2.2 Kiến trúc của mạng

Chúng ta cần xác định kiến trúc của model sử dụng trong quá trình ngược. Có thể thấy, quá trình ngược ở trên yêu cầu ảnh input và ảnh ouput phải có cùng kích cỡ đồng thời chúng ta cũng phải thiết kế sao cho model có thể nắm được semantic của ảnh đầu vào ở mức độ pixel nhằm xác định noise. Tác giả của paper DDPM đã quyết định sử dụng mạng U-Net do nó có thể đáp ứng đầy đủ các yêu cầu trên. 2223

Ảnh: Cấu trúc của mạng U-Net được sử dụng

3. Text-to-Image Generative với Diffusion Model

Diffusion model đã được huấn luyện có thể thực hiện sinh ảnh mới tương tự với ảnh trong phân phối dùng để training từ một nhiễu trắng bất kì, tuy nhiên ảnh được sinh ra hoàn toàn ngẫu nhiên mà ta không thể kiểm soát được các đặc điểm cụ thể, hơn nữa ảnh được sinh ra thường có độ phân giải thấp. Để có thể áp dụng diffusion model cho tác vụ Text-to-image chúng ta cần bổ sung một vài cải tiến.

Classifier Guidance

Là phương pháp làm tăng tính trung thực cũng như chất lượng của hình ảnh với trade-off là giảm sự đa dạng của ảnh được sinh ra. Nhằm bổ sung thêm thông tin về class của ảnh trong quá trình khuyếch tán , trong paper các tác giả đến từ OpenAI có đề xuất bổ sung thêm gradient $c$ của một mô hình classifier đã được training riêng biệt qua đó hướng quá trình sinh ảnh tập trung vào class được target.

Ảnh: Bên trái là ảnh không được guidance, bên phải là ảnh được guidance (Text: "Pembroke Welsh corgi")
Classifier-Free Guidance

Với phương pháp Classifier Guidance bên trên, gradient được lấy từ một pre-trained model riêng biệt . Để tránh việc phụ thuộc vào thông tin từ một pre-trained model khác, phương pháp này huấn luyện một cách đồng thời một mô hình diffusion theo cả 2 mục tiêu là unconditional và conditional bằng cách ngẫu nhiên loại bỏ gradient $c$ trong quá trình training. Cụ thể, predicted noise được định nghĩa:

$\tilde { \epsilon } _ { \theta } ( z _ { t } , c ) = w \epsilon _ { \theta } ( z _ { t } , c ) + ( 1 - w ) \epsilon _ { \theta } ( z _ { t } )$
Trong đó $w$ được gọi là guidance weight, $w$ càng lớn tương ứng với việc tăng sức ảnh hưởng của gradient $c$ .

Note: Imagen đặc biệt chú trọng vào classifier-free guidance để generate ảnh có sự tương quan nhất với text.
Cascaded diffusion models

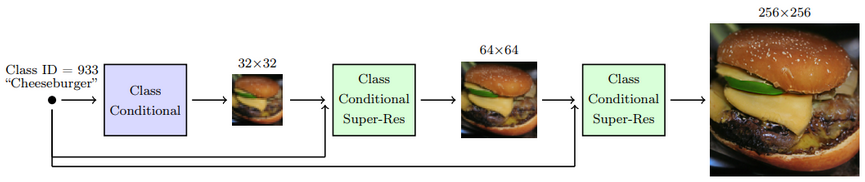
Ảnh được sinh ra bởi mô hình diffusion thường sẽ cho độ phân giải thấp (VD: 32x32), lý do là bởi độ phân giải thấp thì mô hình sẽ tập trung vào việc generate ảnh với các chi tiết và đặc điểm một cách hợp lý nhất, điều này là khó khăn khi gen luôn ra ảnh với độ phân giải cao. Do đó paper này đã đề xuất một cấu trúc nhằm tăng dần độ phân giải của ảnh đươc sinh ra bằng cách sử dụng mô hình thác nước với 3 diffusion model nối tiếp nhau, trong đó 2 model phía sau được sử dụng để tăng độ phân giải.

Ảnh: Cấu trúc của cascaded diffusion model
Ảnh sau khi được sinh ra bởi mô hình đầu tiên sẽ làm input cho model diffusion thứ 2, tương tự đổi với diffusion model cuối cùng. Ngoài ra để việc scale up ảnh đạt hiệu quả tốt nhất, các additional signal sử dụng trong conditional diffusion cũng được bổ sung vào input của từng model.

Các bạn có thể tham khảo thêm về cascaded diffusion models tại đây.
Text-to-Image Model

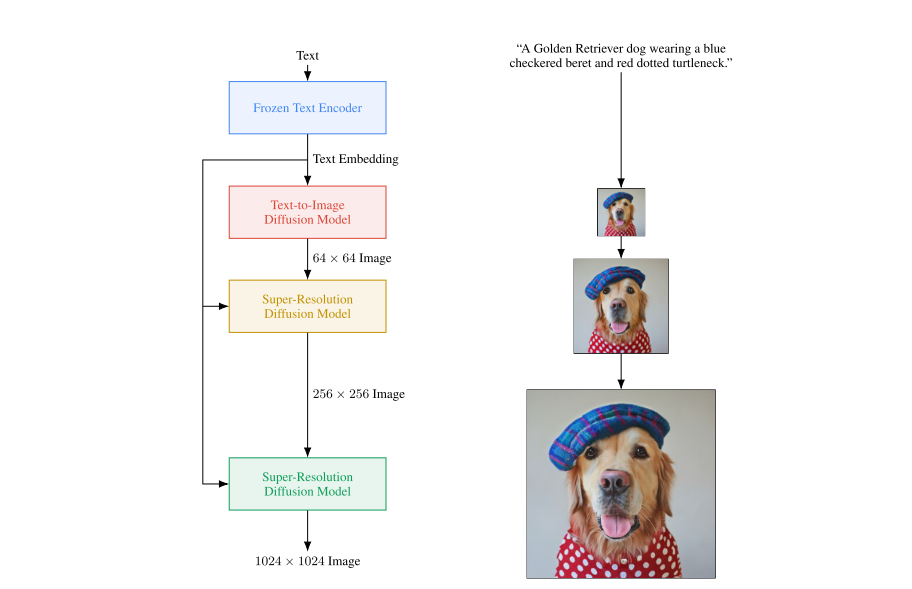
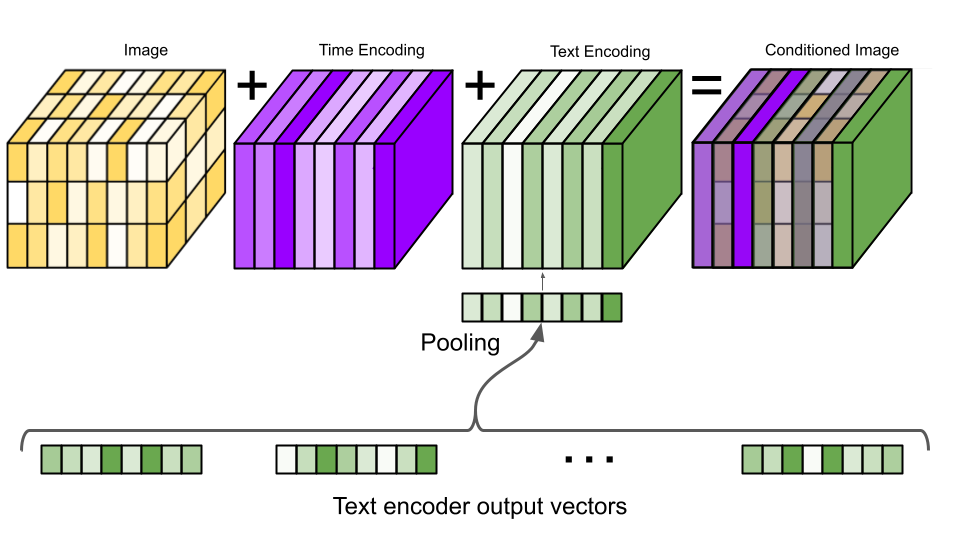
Sử dụng Text Encoder nhằm embedding text input thành vectơ và sử dụng vectơ này làm input cho mô hình Cascaded Diffusion, quá trình generate sẽ sử dụng thông tin từ vectơ text embedding để ảnh được sinh ra giống với mô tả của text.

Ảnh: Flow của mô hình sinh ảnh Imagen

4. Imagen

Sau khi đi qua một vài khái niệm cơ bản giờ hãy phân tích về nhân vật chính của chúng ta. Imagen được train với bộ dữ liệu xấp xỉ 860 triệu cặp image-text, trong đó gồm 400 triệu datapoint lấy từ bộ public Laion và 460 triệu còn lại lấy từ dữ liệu nội bộ của Google. Điểm khác biệt lớn khiến cho Imagen trở thành mô hình text-to-image mạnh nhất có thể kể đến đó là:

Text Encoder sử dụng các mô hình pre-trained language lớn

DALL-E 2, GLIDE hay các mô hình text-to-image trước đó sử dụng Text Encoder được training với bimodal data - tức là data đi theo cặp (image, text caption), ưu điểm là dạng data này giúp mô hình có thể học được sự liên kết giữa ảnh và text tương ứng với nó, tuy nhiên lượng data là quá ít khi so sánh với lượng data thuần text hoặc image . Text Encoder được sử dụng trong Imagen là mô hình Encoder T5-XXL , T5 là pre-trained transformer language models mạnh mẽ và được sử dụng cho rất nhiều tác vụ NLP khác nhau. Mô hình T5 được train với lượng dữ liệu chỉ bao gồm text với lượng data là rất lớn khiến cho Encoder T5 có thể nắm bắt được ngữ nghĩa ẩn của câu text rất hiệu quả. Một điểm đáng chú ý là phần Text Encoder này sẽ được "frezze" trong quá trình training.

Ảnh: Minh họa text embedding được "chèn" vào tại từng step để traning kết hợp với hình ảnh

Threshoding - khắc phục điểm yếu của classifier-free guidance

Việc tăng guidance weight $w$ giúp mô hình có thể cải độ phù hợp giữa ảnh và text (image-text alignment), tuy nhiên khi $w$ quá lớn (VD: $w>5$ ) ảnh được generate sẽ thường trông không tự nhiên hay tệ hơn là ảnh bị bão hòa. Lí do là bởi khi $w$ lớn, ảnh được predict tại từng step có giá trị pixel vượt quá khoảng giá trị pixel của các ảnh trong training data (VD: khoảng [-1,1]). Để giải quyết vấn đề này, tác giả Imagen đã nghiên cứu 2 giải pháp:

Static Thresholding: Thực hiện clipped giá trị các pixel về khoảng [-1,1], cụ thể tất cả các giá trị pixel > 1 sẽ trở thành 1, các giá trị pixel < -1 sẽ trở thành -1.
Dynamic Thresholding: Chọn một số lượng các pixel có giá trị dương (VD: 80% lượng pixel > 0) và threshhold trên giá trị $s$ của các pixel đó. Khi giá trị $s$ đó >1 thì clipped giá trị tất cả các pixel về khoảng $[-s,s]$ , sau đó chia tất cả cho $s$ để scale về khoảng [-1,1].

Ảnh: So sánh các phương pháp thresholding khi guidance weight tăng dần

Phương pháp Dynamic Thresholding tỏ ra cực kỳ hiệu quả với guidance weight $w$ tăng cao, điều này cho phép Imagen tận dụng triệt để Classifier-free guidance để tối ưu image-text alignment, cho ra kết quả cực kỳ chính xác với text được mô tả mà ảnh vẫn trung thực và không bị bão hòa.

Efficient U-Net

Với cascade diffusion model được trình bày ở trên, sau khi đưa qua 2 mạng supper-resolution ảnh thu được có độ phân giải 256x256 nhưng như vậy vẫn chưa đủ. Ảnh được sinh ra bởi Imagen có độ phân giải 1024x1024 và điều này khiến cho mạng U-net trở nên rất nặng với nhiều tham số. Do đó các tác giả đã cải tiến U-Net để có thể tiết kiệm bộ nhớ, cải thiện thời gian training và inference, đó là Efficien U-Net. Một số phương pháp được họ sử dụng: đảo thứ tự của các Downsampling (và Upsampling) với các lớp convolution nhằm giảm số lượng tham số, thêm các residual block khi ảnh ở độ phân giải thấp, scale các skip-connection bởi $1 / \sqrt { 2 }$ ,...

5. Kết luận

Có thể nói rằng generative model nói chung và bài toán text-to-image nói riêng đang là lĩnh vực đang được các ông lớn công nghệ cũng như giới khoa học đặc biệt quan tâm. Các ứng dụng AI vẽ tranh, Deepfake,... sử dụng các mô hình generative đều thu hút được sự tò mò và phấn khích của người dùng. Mô hình mới đây của Google đã đặt một bước tiến mới trong việc cải thiện chất lượng của các mô hình sinh ảnh đồng thời mở ra nhiều hướng đi mới để tiếp tục cải thiện các mô hình này.

6. Phụ lục: Nền tảng toán học đằng sau Diffusion model

Khuếch tán thuận (Foward diffusion process)

Một hình ảnh hay 1 datapoint $x _ { 0 } \sim q ( x )$ với $q(x)$ là phân phối của training data sẽ được thêm nhiễu (noise) lần lượt theo từng step. Ta định nghĩa một quá trình thuận $q \left ( x _ { t } | x _ { t - 1 } \right )$ với $t$ là tham số về mặt thời gian theo từng step, $t$ càng lớn tương ứng với bức ảnh càng nhiều nhiễu.

Cụ thể quá trình thuận:

$q ( x _ { t } | x _ { t - 1 } ) = N ( x _ { t } ; \sqrt { 1 - \beta _ { t } } x _ { t - 1 } , \beta _ { t } I)$
Ở đây ảnh tại step t sẽ được thêm nhiễu Gaussion bằng cách sample ra $x_{t}$ theo phân phối Gauss với kỳ vọng $\sqrt { 1 - \beta _ { t } } x _ { t - 1 }$ và phương sai $\beta _ { t } I$ . Lưu ý rằng $\beta$ ở đây là siêu tham số được thay đổi theo thời gian và kiểm soát bởi variance schedule : $\{ \beta _ { t } \in ( 0 , 1 ) \} _ { t = 1 } ^ { T }$ . Khi số step T đủ lớn, ảnh ban đầu sẽ chuyển thành một ảnh nhiễu trắng hoàn toàn (isotropic noise).
Khuếch tán ngược (Reverse diffusion process)

Nếu chúng ta có thể đảo ngược quá trình bên trên thành $q \left ( x _ { t -1} | x _ { t } \right )$ thì từ một ảnh nhiễu trắng $x _ { T } \sim N ( 0 , I )$ chúng ta có thể tái tạo lại ảnh tương đương với mẫu được lấy trong phân phối $q(x)$ ban đầu. Nhưng thật không may rằng chúng ta không thể tính toán trực tiếp $q \left ( x _ { t -1} | x _ { t } \right )$ do đó chúng ta cần học một model $p _ { \theta }$ có khả năng xấp xỉ quá trình đảo ngược bên trên.

Ta định nghĩa một quá trình ngược:

$p( x _ { t-1 } | x _ { t} )=N ( x _ { t -1} ; \mu _ { \theta } ( x _ { t } , t ),\Sigma _ { \theta } ( x _ { t } , t ) )$
trong đó $\mu _ { \theta }$ và $\Sigma _ { \theta }$ chính là hai tham số mà mô hình của chúng ta cần xấp xỉ. Toàn bộ quá trình biến đổi ngược từ $x _ { T }$ về $x _ { 0 }$ có thể được tính toán nhờ vào tính chất độc lập của chuỗi Markov:

$p _ { \theta } ( x _ { 0:T } ) = p ( x _ { T } ) \prod _ { t = 1 } ^ { T } p _ { \theta } ( x _ { t - 1 } | x _ { t } )$
Quá trình training

Mục tiêu của ta lúc này là minimize hàm negative log-likelihood: $- \log p _ { \theta } ( x _ { 0 } )$ , tuy nhiên hàm này cũng không trực tiếp tính toán được, do đó chúng ta cần sử dụng một kỹ thuật tương tự đã áp dụng với VAE đó là Variational lower bound:

$- \log p _ { \theta } ( x _ { 0 } ) \leq - \log p _ { \theta } ( x _ { 0 } ) + D _ { K L } ( q ( x _ { 1:T } | x _ { 0 } ) \| p _ { \theta } ( x _ { 1:T } | x _ { 0 } ) )$
Chúng ta sẽ gián tiếp minimize hàm $- \log p _ { \theta } ( x _ { 0 } )$ bằng cách minimize đẳng thức phía bên phải.Tiếp tục sử dụng tính chất Bayes và bất đẳng thức Jensen chúng ta có được hàm mục tiêu cần minimize (phần biến đổi này khá dài và phức tạp nên mình không trình bày cụ thể, mình recommend các bạn nên đọc thêm ở link bên dưới để hiểu rõ):

$D _ { K L } ( q ( x _ { T } | x _ { 0 } ) \| p _ { \theta } ( x _ { T } ) ) +\sum_{t=2} ^ { T } D _{ K L } ( q ( x _{ t - 1 } | x _{ t } , x _{ 0 } ) \| p_{ \theta } ( x _{ t - 1 } | x _{ t } ) ) - \log p _{ \theta } ( x _{ 0 } | x _{ 1 } )$
Thành phần KL Divergence đầu tiên có thể tính toán trực tiếp do $p _ { \theta } ( x _ { T }), x_{T}, x_{0}$ và quá trình $q$ chúng ta đã biết, lúc này chúng ta chỉ cần minimize:

$\sum_{t=2} ^ { T } D_{ K L } ( q ( x_{ t - 1 } | x_{ t } , x_{ 0 } ) \| p_{ \theta } (x_{ t - 1 } | x_{ t } ) ) - \log p_{ \theta } ( x_{ 0 } | x_{ 1 } )$
Thành phần KL Divergence đầu tiên so sánh 2 phân phối Gauss $q ( x_{ t - 1 } | x_{ t } , x_{ 0 } )$ và $p_{ \theta } (x_{ t - 1 } | x_{t})$ do đó nó nó có thể tính toán ở dạng closed form. Ở trên ta có nói rằng $q \left ( x _ { t -1} | x _ { t } \right )$ không thể trực tiếp tính toán nhưng thật may là $q ( x_{ t - 1 } | x_{ t } , x_{ 0 } )$ thì lại có thể tính toán được ^^. Cụ thể :

$q ( x _ { t - 1 } | x _ { t } , x _ { 0 } ) = N ( x _ { t - 1 } ; \tilde { \mu } ( x _ { t } , x _ { 0 } ) , \tilde { \beta } _ { t } \Sigma \rangle$
với $\tilde { \mu }$ và $\tilde { \beta }$ có thể tính toán qua Bayes rule:

$\tilde { \beta } = \frac { 1 - \tilde { \alpha } _ { t - 1 } } { 1 - \tilde { \alpha } _ { t } } \cdot \beta _ { t } ; \tilde { \mu } = \frac { 1 } { \sqrt { \alpha _ { t } } } ( x _ { t } - \frac { 1 - \alpha _ { t } } { \sqrt { 1 - \tilde { \alpha } _ { t } } } \epsilon _ { t } )$
Cần nhắc lại rằng, chúng ta đang tìm cách huấn luyện mô hình có thể xấp xỉ được xác suất có điều kiện của quá trình biến đổi ngược $p _ { \theta } ( x _ { t - 1 } | x _ { t } ) = N ( x _ { t - 1 } ; \mu _ { \theta } ( x _ { t } , t ) , \Sigma _ { \theta } ( x _ { t } , t ) )$ . Chúng ta mong muốn $\mu _ { \theta }$ có thể dự đoán được $\tilde { \mu } _ { t }$ , một phương pháp đơn giản được sử dụng để tính toán lỗi đó là MSE loss:

$L _ { t } = { \mathrm { E } } _ { x _ { 0 } , \epsilon } [ \frac { 1 } { 2 \| \Sigma _ { \theta } ( x _ { t } , t ) \| ^ { 2 } } \| \tilde { \mu } _ { t } ( x _ { t } , x _ { 0 } ) - \mu _ { \theta } ( x _ { t } , t ) \| ^ { 2 } ]$
Và vì $\tilde { \mu } _ { t }$ và $\mu _ { \theta }$ có thể tính toán thông qua noise $\epsilon _ { t }, \epsilon_{\theta}$ và input $x_{t}$ theo từng step, cuối cùng mô hình chỉ cần predict ra noise đã được thêm vào:

$L _ { t } ^ { \operatorname { s i m p l e } } = E _ { t \sim [ l , T ] , x _ { 0 } , \epsilon _ { t } } [ \| \epsilon _ { t } - \epsilon _ { \theta } ( x _ { t } , t ) \| ^ { 2 } ]$
Chi tiết phần biến đổi toán học các bạn có thể tham khảo tại đây.

Khi đã xác định được noise đã được thêm vào trong quá trình thuận, tại từng step chúng ta có thể thu được ảnh bớt nhiễu bằng cách lấy ảnh nhiễu "trừ" đi noise.