Đã đăng vào thg 9 13, 2019 5:06 CH 6 phút đọc

3.0K

Giới thiệu về Connectionist Temporal Classification (CTC) (Phần 2)

Bài đăng này đã không được cập nhật trong 5 năm

Hello guys, bài viết này mình sẽ tiếp nối phần 1, đó là các giải thuật decoding để tìm alignment $h(x)$ phù hợp nhất và tính hàm mất mát ctc (ctc loss function).

Ở bài viết này mình sẽ nêu ra 3 giải thuật ngày nay người ta hay sử dụng: Greedy Decoding, Beam Search Decoding và Beam Search Decoding with Language Model Rescoring.

Best Path Decoding (Greedy Decoding)

Ý tưởng của giải thuật này là:

Ở mỗi time-step, chọn ký tự có xác suất lớn nhất và kết hợp chúng lại với nhau (path có xác suất lớn nhất)
Sau đó, loại bỏ những ký tự trùng nhau (duplicate) và các ký tự trống (blanks) để cho ra kết quả cuối cùng là một chuỗi các từ được dự đoán.

Biểu diễn bằng toán học thì ta có:

$\begin{aligned} \pi^\star &= arg \max_{\pi \in N^T} p(\pi \lvert x) \\ h(x) &= B(\pi^\star) \\ O(S, \mathcal{N_w}) &= - \sum_{(x,z) \in S} ln(\pi^\star) \end{aligned}$

Trong đó:

$\pi$ là path (mỗi path là một cách chọn ký tự ở mỗi time-step rồi kết hợp chúng lại với nhau)
$h(x)$ là alignment
$O$ là ctc loss function (objective function)
$B$ là hàm loại bỏ các ký tự trùng nhau và ký tự trống
$S$ là tập huấn luyện, gồm các cặp chuỗi $(x,z)$
$N^T$ là tập hợp tất cả các path có độ dài là $T$
$\mathcal{N_w}$ đại diện cho vector trọng số của neural network.

Để hiểu rõ hơn, mình sẽ cho một ví dụ như sau:

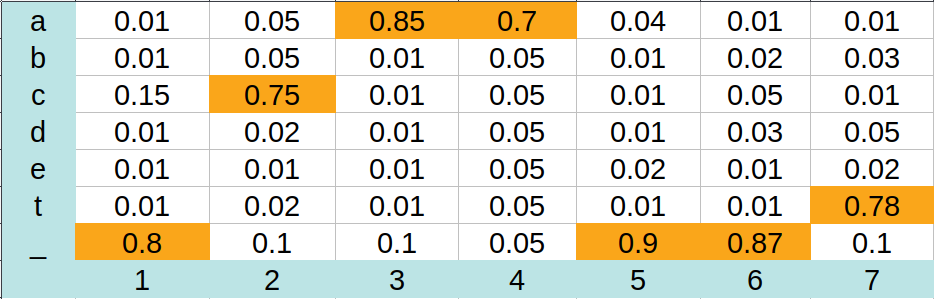
Những con số nền vàng là xác suất cao nhất trong mỗi time-step. Với giải thuật này thì ta sẽ chọn được chuỗi các ký tự là: "_caa__t", sau đó ta loại bỏ đi các ký tự trùng nhau và ký tự trống để cho ra chuỗi hoàn chỉnh là: "cat".

Greedy Decoding là một giải thuật nhanh và đơn giản, nhưng nó không cover được hết tất cả các tình huống, chẳng hạn như:

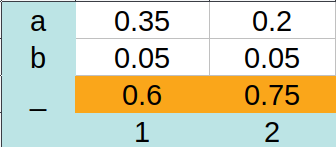
Ở đây ta thấy $p(a|x) = p("aa"|x) + p("a\_"|x) + p("\_a"|x) = 0.35 \times 0.2 +0.35 \times 0.75 + 0.6 \times 0.2 = 0.4525$ mà khi sử dụng greedy ta được $p(""|x) = 0.6 \times 0.75 = 0.45$ , đáng lẽ ta phải decode ra được "a" thay vì "". Do đó, ta cần một giải thuật tốt hơn.

Prefix Search Decoding (Beam Search Decoding)

Pseudocode của giải thuật này như sau:

Data: NN output matrix mat, BW
Result: decoded text
beams = { null };
P_b(null, 0) = 1;
for t = 1 to T do
    bestBeams = bestBeams(beams, BW);
    beams = {};
    for b in bestBeams do
        if !b.isEmpty() then
            P_nb(b, t) += P_nb(b, t-1) * mat(b[-1], t);
        end
        P_b(b, t) += P(b, t-1) * mat(blank, t);
        for c in alphabet do
            b' = b + c;
            if b(t) == c then
                P_nb(b', t) += P_b(b, t-1) * mat(c, t);
            else
                P_nb(b', t) += P(b, t-1) * mat(c, t);
            end
            beams.add(b');
        end
    end
end
return bestBeams(beams, 1)

Đầu tiên ta khởi tạo một bộ beam rỗng và score tương ứng. Ở mỗi time-step, chỉ có $BW$ (beam width) số beam có score tốt nhất được giữ lại. Đối với từng beam được chọn đó, ta tính score của nó ở time-step hiện tại, sau đó mở rộng beam đó với mọi ký tự trong alphabet và tính score ứng với từng beam được mở rộng đấy. Giải thuật trả về kết quả là một beam có score tốt nhất sau khi lặp hết time-step.

Tính beam's score

Ta gọi xác suất của tất cả các path ứng với beam $b$ tại time-step $t$ kết thúc bằng ký tự blank là $P_b(b,t)$ và ký tự không phải blank là $P_{nb}(b,t)$ . Khi đó, score là xác suất của beam $b$ tại time-step $t$ và sẽ là $P(b,t) = P_b(b,t) + P_{nb}(b,t)$ . Cả $P_b$ và $P_{nb}$ đều được khởi tạo bằng $0$ .

Khi ta mở rộng một path (mở rộng một beam) thì ta có ba cách: mở rộng bằng ký tự trống, bằng ký tự giống ký tự cuối và bằng một ký tự khác ngoài hai cái trên. Do đó ta sẽ có hai trường hợp là copy và extend như hình dưới đây:

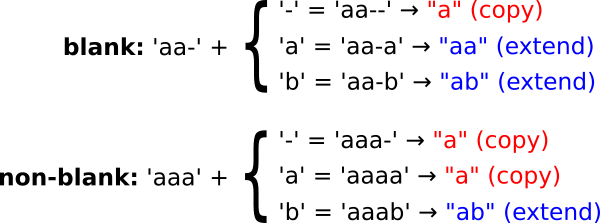
Copy beam

Copy beam là trường hợp mở rộng beam mà khi áp dụng hàm $B$ lên trước và sau khi mở rộng thì kết quả không thay đổi.

Khi mở rộng bằng ký tự trống (blank) của một beam kết thúc bằng ký tự trống, ta sẽ cập nhật $P_b(b,t) = P(b,t-1) \times mat(blank, t)$ . Ta sử dụng $P(b,t-1)$ bởi vì ký tự cuối trước khi mở rộng có thể là blank hoặc non-blank.

Khi mở rộng bằng ký tự giống ký tự cuối của một beam kết thúc không phải blank, nếu beam đó không rỗng, ta cập nhật $P_{nb} = P_{nb}(b,t-1) \times mat(b[-1],t)$ . Ta lấy $P_{nb}(b,t-1)$ bởi vì không ký tự kết thúc đó không phải blank.

Extend beam

Extend beam là trường hợp mở rộng beam mà khi áp dụng hàm $B$ lên trước và sau khi mở rộng thì kết quả khác nhau.

Khi mở rộng bằng ký tự $c$ khác blank và ký tự cuối thì ta cập nhật $P_{nb}(b+c,t) = P(b,t-1) \times mat(c,t)$ . Ta lấy $P(b,t-1)$ bởi vì ký tự cuối trước khi mở rộng là blank hay non-blank thì sau khi mở rộng kết quả vẫn như nhau, nên ta lấy cả hay trường hợp blank và non-blank.

Khi mở rộng bằng ký tự $c$ giống ký tự cuối thì ta cập nhật $P_{nb}(b+c,t) = P_b(b,t-1) \times mat(c,t)$ . Ta lấy $P_b(b,t-1)$ bởi vì để cho ra kết quả khác thì phải thêm blank vào giữa hai ký tự giống nhau, ví dụ: "a_a".

Tính loss (objective) function

Nhìn vào mã giả, ta không thấy chỗ nào tính loss function cả, vì thế câu hỏi được đặt ra là giải thuật này cho ra loss function như thế nào? Như mình đã nói ở phần 1, loss function được tính bằng negative log likelihood của alignment tìm được:

$O(S, \mathcal{N_w}) = - \sum_{(x,z) \in S} ln(p(l|x))$

$p(l|x)$ ở đây sẽ là $P(b, T)$ hay còn gọi là score được tính cuối cùng với $b = bestBeams(beams, 1)$ là kết quả của giải thuật này.

Beam Search Decoding with Language Model Re-scoring

Đúng với cái tên, giải thuật này là beam search decoding nhưng chỉ có thay đổi ở phần tính toán beam's score bằng cách thêm N-gram Character-level Language Model.

Mình sẽ nói ngắn gọn về Language Model (LM) này, chi tiết hơn thì mình sẽ viết một bài khác nói riêng về LM ở đây.

N-gram Char-level LM sẽ tính xác suất của một câu $s$ trên tập dữ liệu huấn luyện dựa trên xác suất của từng ký tự trong câu đó, với xác suất của từng ký tự được tính khi đã biết $N-1$ ký tự đứng trước nó:

$p_{LM}(s = \{c_1,c_2,...,c_K\}) = p(c_1)p(c_2|c_1)...p(c_K|c_{K-N+1}...c_{K-1})$

Khi áp dụng vào beam search decoding, $s$ sẽ là $b'$ (beam được mở rộng bằng một ký tự trong alphabet) và score sẽ được tính lại (rescore) là $P(b',t) = p_{LM}(b')$ . Cuối cùng ta có pseudocode như sau:

Data: NN output matrix mat, BW, LM
Result: decoded text
beams = { null };
P_b(null, 0) = 1;
for t = 1 to T do
    bestBeams = bestBeams(beams, BW);
    beams = {};
    for b in bestBeams do
        if !b.isEmpty() then
            P_nb(b, t) += P_nb(b, t-1) * mat(b[-1], t);
        end
        P_b(b, t) += P(b, t-1) * mat(blank, t);
        for c in alphabet do
            b' = b + c;
            P(b', t) = applyLM(LM, b, c); // Add LM rescoring
            if b(t) == c then
                P_nb(b', t) += P_b(b, t-1) * mat(c, t);
            else
                P_nb(b', t) += P(b, t-1) * mat(c, t);
            end
            beams.add(b');
        end
    end
end
return bestBeams(beams, 1)

Tham khảo