Giới thiệu

Vào năm 2017, trí tuệ nhân tạo AlphaGo Zero (AGZ) do Deepmind phát triển đã đánh bại cao thủ cờ vây Lee Sedol (người đã từng 18 lần vô địch cờ vây thế giới và được coi là người chơi cờ vây giỏi nhất trong vòng 1 thập kỳ qua) với tỷ số 4-1. Sự kiện này đã gây chấn động rất lớn tới những người quan tâm đến trí tuệ nhân tạo vì từ trước tới nay con người vẫn luôn tự tin độ phức tạp của cờ vây (số khả năng có thể xảy ra trong một ván cờ nhiều hơn cả số nguyên tử trong vũ trụ!) khiến các thuật toán tìm kiếm của máy tính không bao giờ có thể đánh bại được. Ấy vậy mà chỉ với 40 ngày huấn luyện, trí tuệ nhân tạo AGZ đã đặt dấu chấm hết cho bề dày 2500 năm kinh nghiệm cờ vây của con người. Phiên bản trước của AGZ, AlphaGo, cũng là một AI mạnh mẽ đã chiến thắng cao thủ khác là Ke Jie. Tuy nhiên, phiên bản này đòi hỏi các kỹ sư DeepMind tạo ra hàng nghìn thế cờ chuyên nghiệp cho quá trình huấn luyện AI. Trong khi đó, AGZ lại không cần học bất cứ một thế cờ nào từ trước, thậm chí ở giai đoạn đầu "nó" còn không biết chơi cờ vây. Đó chính là lý do cho chữ "Zero" trong tên nó - bắt đầu từ con số 0; và từ con số 0 này, AGZ tự chơi với chính mình hàng triệu ván cờ trước khi trở thành AI cờ vây mạnh nhất thế giới.

(Trong bài này mình sẽ sử dụng một số thuật ngữ và kiến thức cơ bản của reinforcement learning, nếu bạn chưa tìn hiểu về RL cơ bản thì có thể tham khảo bải viết trước của mình: Giới thiệu về học tăng cường và ứng dụng Deep Q-Learning chơi game CartPole)

Điều gì khiến AGZ mạnh mẽ đến như vậy? 3 thành phần:

1. Mạng học sâu: nhận input là state hiện tại, đầu ra tách thành 2 nhánh trả về value (phần trăm thắng) và policy (nước đi tiếp theo).
2. Monte Carlo Tree Search (MTCS): là một thuật toán tìm kiếm các bước di chuyển tiềm năng nhất dựa trên các thông tin từ mạng học sâu. Một mạng học sâu nếu được train tốt sẽ giúp MTCS loại bỏ phần lớn các nước đi kém, khiến nó không phải brute-force như các engine cờ truyền thống.
3. Self-play: AGZ chơi với chính nó qua một số ván cờ và cập nhật phiên bản có tỉ lệ thắng cao hơn.

(4. Phần này cung quang trọng không kém nhưng lại không thuộc phạm trù thuật toán và bạn cũng không thể implement được: đó là tiền . AGZ được train bằng 4 TPUs của google trong 40 ngày, tính ra đâu đó tầm 20.000.000$ )

Tổng quan

David Foster - founder của Applied Data Science phân tách AGZ thành các phần nhỏ và tạo ra cheatsheet rất trực quan và đầy đủ về AGZ. Link ảnh chất lượng cao tại đây

Training pipeline

Quá trình huấn luyện AGZ gồm 3 bước thực hiện song song:

Self-play

Bước này AGZ tự chơi với chính nó để thu thập dữ liệu trận đấu, phục vụ training mạng học sâu. Tất nhiên ở những ván cờ đầu tiên, AGZ chơi rất "ngây thơ" vì output mạng học sâu lúc này (cả value và policy) chỉ là những giá trị random. Nhưng chơi càng lâu, AGZ càng trở nên xuất sắc. Thuật toán chơi tổng cộng 25000 games với chính nó, sử dụng MCTS để chọn nước đi (mình sẽ nói rõ hơn ở mục Monte Carlo Tree Search). Mỗi nước đi, các giá trị sau được lưu lại:

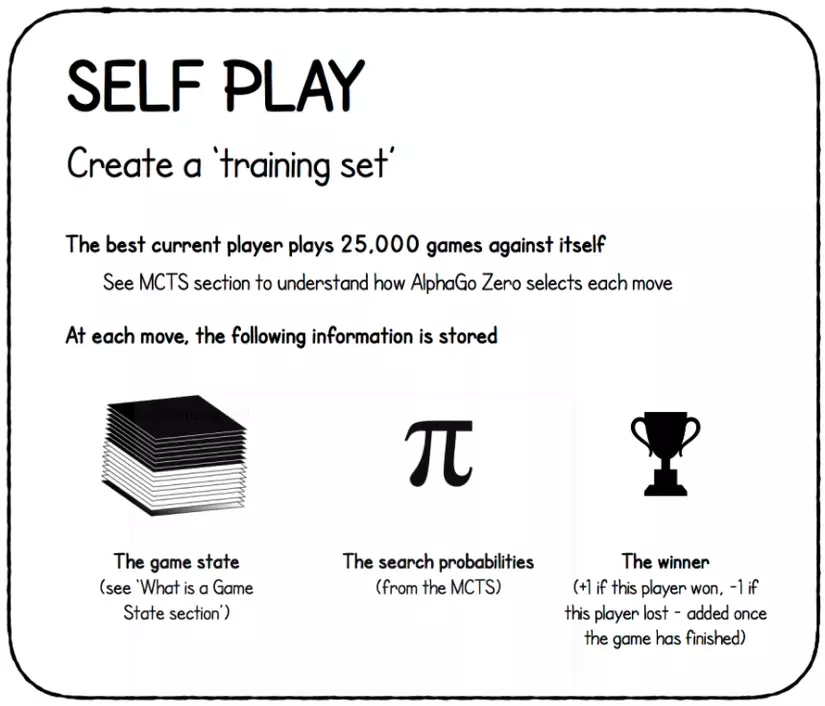
• Game state: (chi tiết xem phần mạng học sâu)
• Action probabilities: Phân bố xác suất các hành động kế tiếp. Tuy nhiên nên tránh nhầm lẫn với phân bố xác suất từ nhánh policy của mạng học sâu. Phân bố này tính toán từ MCTS.
• The winner: +1 nếu lượt này thắng, -1 nếu lượt này thua. Giá trị này chỉ xuất hiện khi game kết thúc.

Retrain network

Dựa trên bộ dữ liệu đã thu thập (và được update liên lục) từ quá trình self-play, thuật toán thực hiện train lại mạng neuron và tối ưu trọng số mạng. Vòng lặp training diễn ra như sau:

1. Sample mini-batch 2048 nước đi (là bộ 3 thông tin ở phần trên) từ 500000 games mới nhất, lấy game state làm input cho mạng.
2. Train mạng với bộ dữ liệu này
3. Như đã đề cập ở phần giới thiệu, mạng học sâu này gồm 2 nhánh là value và policy; vậy nên nó cần 2 hàm loss để backprop. Policy loss là cross-entropy giữa phân bố xác suất policy do mạng dự đoán và phân bố xác suất policy thực tế do MCTS tính được. Value loss là mean-squared error giữa predicted value và value của MCTS tính toán.
4. Optimizer sử dụng là SGD với Momentum thay vì Adam
5. Evaluate mạng sau mỗi 1000 vòng lặp

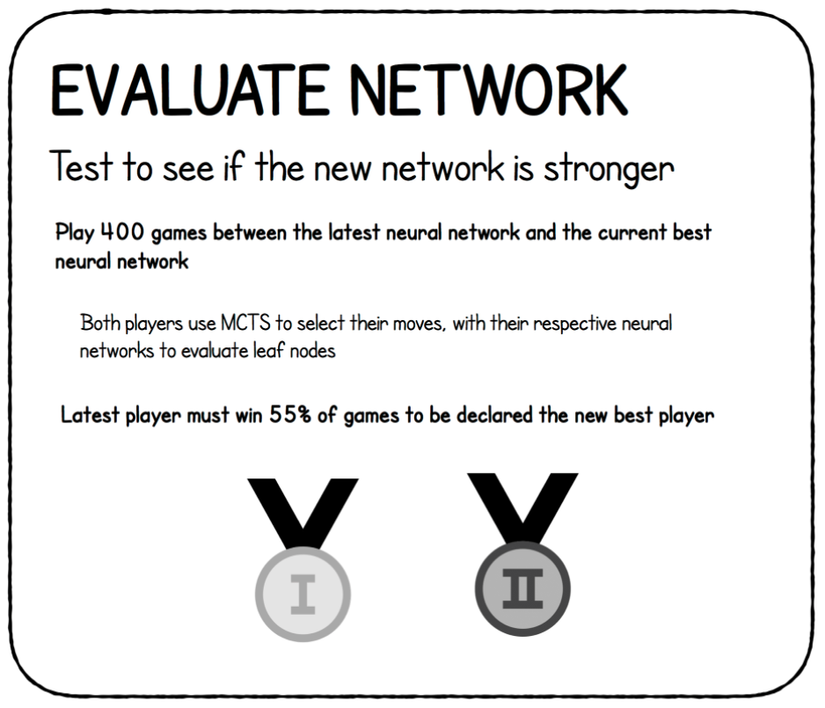
Evaluate network

Bước này ta thực hiện đánh giá mô hình học sâu mới train để xem liệu nó có tốt hơn phiên bản tốt nhất không. Hai mạng sẽ được "đấu" với nhau 400 games, cả 2 đều sử dụng MCTS để chọn nước đi. Mô hình mới train phải thắng ít nhất 55% số ván đấu để trở thành "người chiến thắng", khi đó trọng số của mạng được cập nhật theo trọng số mới nhất.

Monte Carlo Tree Search

Ở phần trước mình đã nói một cách tổng quan về cách AGZ chọn từng bước đi. Tại một thế cờ, thay vì brute-force tất cả các nước đi và mở rộng cây tìm kiếm từ các nước đó (rất tốn kém), AGZ sử dụng mạng học sâu để lọc ra một vài nước đi tốt nhất để mở rộng. Trong phần này mình sẽ nói kỹ hơn về cách thuật toán MCTS.

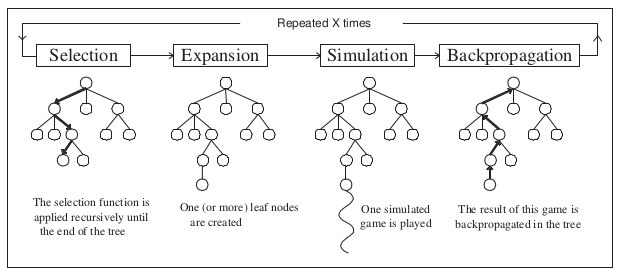
Thuật toán MCTS bao gồm 4 bước:

1. Selection: Từ node gốc, chọn đường đi tiềm năng nhất (dựa trên một vài statistics) cho đến khi gặp node lá.
2. Expansion: Tạo một node lá từ nốt hiện tại
3. Simulation: Mở rộng đến khi game kết thúc
4. Backup (back propagation): Lưu lại đường đi này và update statistics của các cạnh trên path đã chọn theo hướng từ dưới lên trên (từ node lá đến node gốc).

Lặp lại các bước này X lần ta sẽ có 1 cây với node gốc là state hiện tại và từ đó chọn ra nước đi tiếp theo tốt nhất dựa trên statistics của cây.

Tree statistics

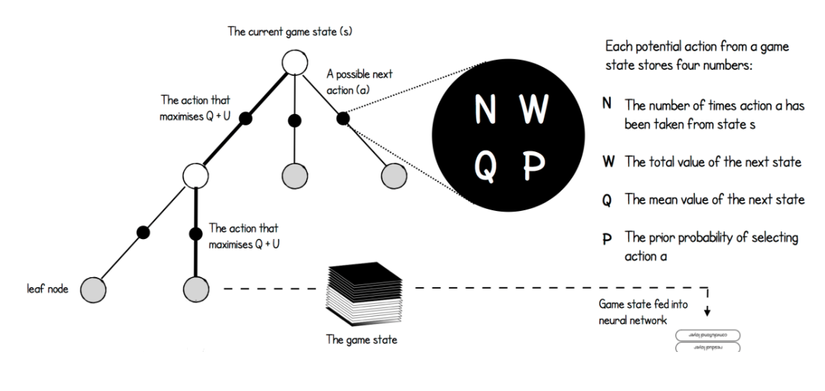
Với MCTS trong AGZ, mỗi cạnh là một action và có 4 statistics:

• N: Số lần action a được chọn tại state s.
• W: Tổng value của state tiếp theo. Mỗi khi ta đến node lá MCTS query mạng neuron để lấy value của state đó; và trong quá trình backup, giá trị này cộng dồn (từ dưới lên trên) vào W của các node trên đường đi.
• Q: value trung bình của state. Đơn giản là lấy W/N. Ý tưởng của Q cũng tương tự như Q-value trong Q-learning.
• P: Prior probabilities lựa chọn action a tại state s. Giá trị này lấy từ nhánh policy của mạng học sâu.

Và đó là những concept cơ bản của MCTS. Phần tiếp theo chúng ta sẽ đi sâu vào cơ chế hoạt động của nó.

Cơ chế hoạt động

Bắt đầu với node gốc đại diện cho state hiện tại, MCTS chọn action có $(Q + U)$ lớn nhất với $Q$ là value trung bình của state tiếp theo, $U$ là một hàm của $P$ và $N$ trong đó $U$ tăng khi action đó chưa được chọn nhiều (exploration) hoặc prior probability của action đó cao (exploitation).

Cụ thể, $U$ được tính như sau:

$$U(s, a)=c_{p u c t} \cdot P(s, a) \cdot \frac{\sqrt{\left.\sum_{b} N(s, b)\right)}}{1+N(s, a)}$$

, trong đó $N(s,a)$ là số lần chọn action a từ state s, $c_{p u c t}$ là hyperparameter điều chỉnh trade-off giữa exploration và exploitation. Trong paper AGZ tác giả chọn $c_{p u c t}=1.0$.

Bước 2, ta tiếp tục mở rộng đến khi gặp node lá (terminal state). Game state của node này được đưa vào mạng neuron để predict ra hai giá trị p (phân bố xác suất các nước đi kế tiếp - lấy từ nhánh policy) và v (value của state này - lấy từ nhánh value).

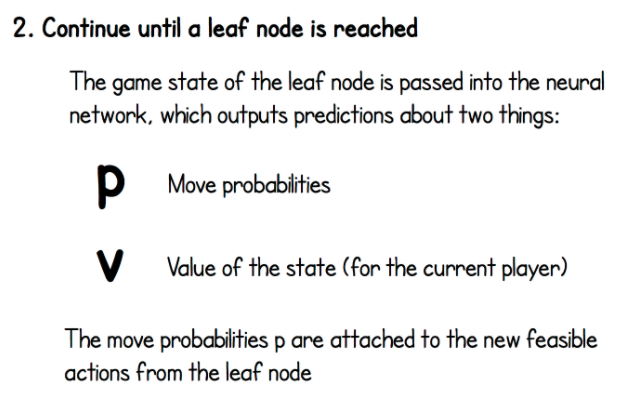
Bước 3, backup các cạnh trước đó cho đến tận node gốc. Duyệt từ node lá, mỗi cạnh đã đi qua sẽ được update như sau:

• Tăng N (số lần đi qua) lên 1
• Cộng W với v lấy từ mạng neuron
• Tính $Q=W/N$

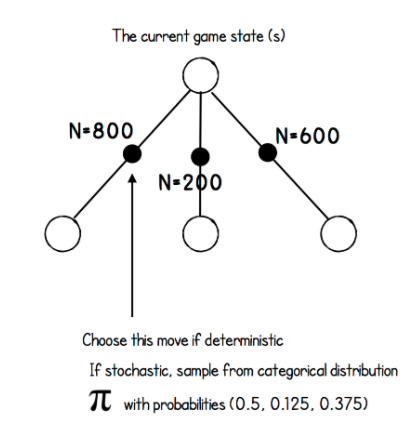
Với mỗi bước đi, ta lặp 3 bước trên 1600 lần để xây dựng cây trước khi chọn ra nước đi kế tiếp. Cách chọn nước đi kế tiếp từ cây đã xây dựng như sau:

Khi thi đấu hoặc trong quá trình evaluate performance, ta chọn một cách "chắc cú" (deterministic): chọn action có giá trị N lớn nhất. Tuy nhiên trong quá trình training, ta sẽ muốn thêm vào một chút yếu tố ngẫu nhiên để buộc agent explore các khả năng có thể xảy ra. Để tạo ra các nước đi ngẫu nhiên, ta tính xác suất chọn action bằng công thức sau:

$$\pi(a \mid s)=\frac{N(s, a)^{1 / \tau}}{\sum_{b} N(s, b)^{1 / \tau}}$$

, trong đó $\tau$ là thông số nhiệt độ kiểm soát mức độ exploration, được khởi tạo bằng 1.0 ở đầu game và giá trị giảm dần sau một số lần di chuyển nhất định.

Cuối cùng, sau khi chọn xong nước kế tiếp:

• Nước được chọn trở thành node gốc.
• Giữ lại tất cả lá gắn với node gốc này.
• Loại bỏ tất cả phần khác.
• Lặp lại từ đầu cho đến khi ván đấu kết thúc.

Deep Neural Network

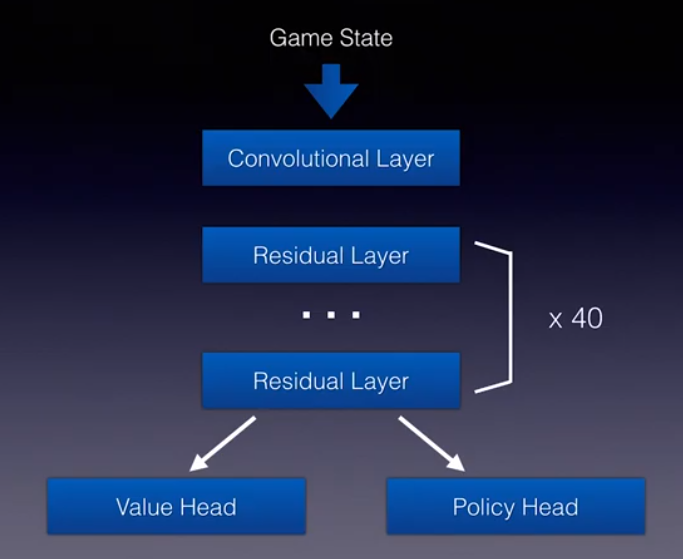
Để MCTS hoạt động hiệu quả, cần có sự hỗ trợ rất lớn từ mạng học sâu để làm giảm không gian tìm kiếm. Còn MCTS (bản chất thống kê) có thể đưa ra ground truth đáng tin cậy giúp ổn định quá trình huấn luyện mạng học sâu. AGZ sử dụng kiến trúc ResNet, đầu vào là game state, qua một convolution layer vào 40 residual layer trước khi tách 2 nhánh value và policy. Đây chính là kiến trúc Actor-Critic trong RL. Vì 2 lớp convolution và residual khá phổ biến nên mình sẽ không nói lại về 2 lớp này mà chỉ tập trung vào policy head và value head.

Game state

Bàn cờ Go có kích thước 19x19 nên kích thước 1 channel state cũng là 19x19. Vị trí của tất cả quân đen ở state hiện tại được encode dưới dạng lưới: 1 nếu có quân đen và 0 ngược lại. Ngoài state hiện tại, AGZ còn stack thêm 7 state trước đó. Vậy nên ta sẽ có 8 state cho quân đen và tương tự với quân trắng. Channel cuối cùng thể hiện lượt đi tại state đó: tất cả bằng 1 nếu lượt đen, bằng 0 nếu lượt của trắng. Kết quả là ta có game state kích thước 19x19x17.

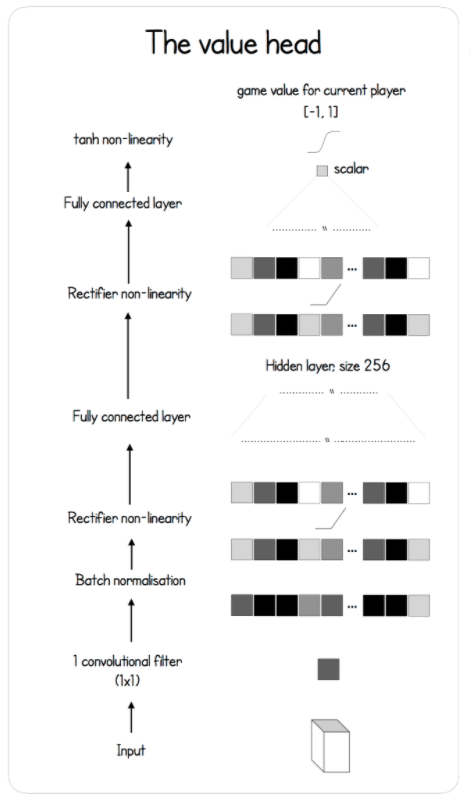
Value head

Input đưa thẳng qua 1 lớp convolution 1x1, tiếp theo là batch norm và ReLU. Sau đó là 1 lớp fully connected với 256 units, 1 lớp ReLU; và lại đi qua 1 lớp convolution nữa. Activation lúc này là tanh để co giá trị vể [-1, 1]

Policy head

Input được đưa qua một lớp convolution 2 filters 1x1, sau đó đi qua batch norm, ReLU và mạng fully connected. Mạng dự đoán xác suất cho từng ô vuông trong bàn cờ 19x19

Kết

Và đó là tất cả những thuật toán bên trong siêu AI AlphaGo Zero. Cá nhân mình thấy thuật toán này rất thú vị, đặc biệt là sự kết hợp cực kỳ khôn ngoan và tinh tế giữa một thuật toán tìm kiếm cổ điển Monte Carlo Tree Search và một mô hình hiện đại ResNet. Mong rằng qua bài này các bạn sẽ cảm thấy thích Reinforcement Learning hơn. Cảm ơn đã đọc đến đây.