Đánh giá các mô hình học máy
Bài đăng này đã không được cập nhật trong 4 năm
Abstract
Trong quá trình xây dựng một mô hình Machine Learning, một phần không thể thiếu để xét xem mô hình có chất lượng tốt hay không chính là đánh giá mô hình. Đánh giá mô hình giúp chúng ta chọn lựa được các mô hình phù hợp với bài toán cụ thể. Để có thể áp dụng đúng thước đo đánh giá mô hình phù hợp, chúng ta cần hiểu bản chất, ý nghĩa cũng như các trường hợp sử dụng nó. Cùng phân tích và tìm hiểu các thước đo này nhé!
Mong rằng bài viết này của mình sẽ giúp các bạn hiểu hơn về các Metric đánh giá mô hình học máy ^^
Để rõ ràng hơn, mình sẽ tập trung phân tích các metric đánh giá đối với: mô hình phân loại (classification), mô hình hồi quy (regression) và xếp hạng (Ranking)
Bài toán phân loại (Classification)
Classifcation là một bài toán được sử dụng vô cùng rộng rãi trong Machine Learning với các tính ứng dụng đa dạng như nhận diện khuôn mặt, phân loại video Youtube, phân loại văn bản, phân loại giọng nói, …
Có thể kể tới một vài mô hình tiêu biểu như Support Vector Machine (SVM), Logistic Regression, Decision Trees, Random Forest, XGboost, … Dưới đây là một số metrics để đánh giá mô hình phân loại mà mình sưu tầm được:
Confusion Matrix (Đây không phải là 1 metric, nhưng rất quan trọng)
Chúng ta cùng tìm hiểu một thuật ngữ cơ bản được sử dụng trong các bài toán phân loại – Confusion matrix (AKA error matrix). Nó thể hiện được có bao nhiêu điểm dữ liệu thực sự thuộc vào một class, và được dự đoán là rơi vào một class. Để dễ hiểu hơn, chúng ta cùng làm một ví dụ nhé
Ví dụ một bài toán phân loại ảnh đó là mèo hay không, trong dữ liệu dự đoán có 100 ảnh là mèo, 1000 ảnh không phải là mèo. Ở đây, kết quả dự đoán là như sau
Trong 100 ảnh mèo dự đoán đúng 90 ảnh, còn 10 ảnh được dự đoán là không phải. Nếu ta coi cat là “positive” và non-cat là “negative”, thì 90 ảnh được dự đoán là cat, được gọi là True Positive, còn 10 ảnh được dự đoán non-cat kia được gọi là False Negative
Trong 1000 ảnh non-cat, dự đoán đúng được 940 ảnh là non-cat, được gọi là True Negative, còn 60 ảnh bị dự đoán nhầm sang cat được gọi là False Positive
Có thể tới đây nhiều người sẽ khá là lẫn lộn, “True”, “False” rồi “Positive”, “Negative”. Vậy để có một cách dễ nhớ, có một mánh nhỏ như sau
- True/False ý chỉ những gì ta đã dự đoán là đúng hay chưa
- Positive/Negative chỉ những gì ta dự đoán (có hoặc không) Nói cách khách, nếu thấy chữ True tức là dự đoán là đúng (là cat hay non-cat, chỉ cần đúng), còn False thì ngược lại.
Classification Accuracy
Đây là độ đo của bài toán phân loại mà đơn giản nhất, tính toán bằng cách lấy số dự đoán đúng chia cho toàn bộ các dự đoán. Ví dụ với bài toán Cat/Non-cat như trên, độ chính xác sẽ được tính như sau:
Classification Accuracy = (90+940)/(1000+100) = 93.6%
Nhược điểm của cách đánh giá này là chỉ cho ta biết được bao nhiêu phần trăm lượng dữ liệu được phân loại đúng mà không chỉ ra được cụ thể mỗi loại được phân loại như thế nào, lớp nào được phân loại đúng nhiều nhất hay dữ liệu của lớp nào thường bị phân loại nhầm nhất vào các lớp khác.
Precision
Như đã nói phía trên, sẽ có rất nhiều trường hợp thước đo Accuracy không phản ánh đúng hiệu quả của mô hình. Giả sử mô hình dự đoán tất cả 1100 ảnh là Non-cat, thì Accuracy vẫn đạt tới 1000/1100 = 90.9%, khá cao nhưng thực chất mô hình khá là tồi Vì vậy chúng ta cần một metric có thể khắc phục được những yếu điểm này. Precision là một trong những metrics có thể khắc phục được, công thức như sau:

Áp dụng vào bài toán Cat/Non-cat, Precision sẽ được tính như sau:
Precision(cat) = 90/(90+60) = 60% Precision(non-cat) = 940/(940+10) = 98.9%
Có thể thấy việc dự đoán Cat chưa thực sự tốt nhờ phép đó Precision này. Precision sẽ cho chúng ta biết thực sự có bao nhiêu dự đoán Positive là thật sự True
Recall
Recall cũng là một metric quan trọng, nó đo lường tỷ lệ dự báo chính xác các trường hợp positive trên toàn bộ các mẫu thuộc nhóm positive. Công thức của Recall như sau:

Áp dụng vào bài toán Cat/Non-cat, Precision sẽ được tính như sau:
- Recall(cat) = 90/(90+10) = 90%
- Recall(non-cat) = 940/(940+60) = 94%
Recall cao đồng nghĩa với việc True Positive Rate cao, tức là tỷ lệ bỏ sót các điểm thực sự là positive là thấp
F1-score
Tùy thuộc vào bài toán mà bạn sẽ muốn ưu tiến sử dụng Recall hay Precision. Nhưng cũng có rất nhiều bai toán mà cả Precision hay Recall đều quan trọng. Một metric phổ biến đã kết hợp cả Recall và Precision lại được gọi là F1-score
F1-score được tính theo công thức sau:
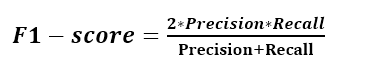
Sensitivity – Specificity
Sensitivity và Specificity là 2 metrics được sử dụng trong các bài toán phân loại liên quan đến y tế và sinh học. Chúng được định nghĩa như sau:

AUC
AUC (Area Under the Curve) là một phép đo tổng hợp về hiệu suất của phân loại nhị phân trên tất cả các giá trị ngưỡng có thể có. Để hiểu rõ hơn về metric này, chúng ta sẽ tìm hiểu về một khai niệm cơ sở trước, đó là ROC Curve
ROC Curve (The receiver operating characteristic curve) là một đường cong biểu diễn hiệu suất phân loại của một mô hình phân loại tại các ngưỡng threshold. Về cơ bản, nó hiển thị True Positive Rate (TPR) so với False Positive Rate (FPR) đối với các giá trị ngưỡng khác nhau. Các giá trị TPR, FPR được tính như sau:

Cùng làm một ví dụ cho dễ hình dung nhé
Có rất nhiều mô hình phân loại mang tính xác suất, ví dụ dự doán xác suất của một mẫu là Cat. Chúng so sánh xác suất đầu ra với một số ngưỡng giới hạn và nếu nó lớn hơn ngưỡng đó, mô hình dự đoán nhãn là Cat, còn không thì là Non-cat.
Ví dụ mô hình của bạn dự đoán giá trị xác suất cho 4 samples lần lượt là [0.45, 0.6, 0.7, 0.3]. Tùy vào giá trị ngưỡng mà sẽ có các nhãn đầu ra dự đoán khác nhau:
- Ngưỡng là 0.5: Sample 2,3 là Cat
- Ngưỡng là 0.25: Tất cả samples đều là Cat
- Ngưỡng là 0.8: Tất cả sample là Non-cat
Có thể thấy với các ngưỡng khác nhau, chúng ta sẽ có kết quả dự đoán nhãn khác nhau, kéo theo các giá trị như precision hay recall cũng sẽ khác nhau
ROC tìm ra TPR và FPR ứng với các giá tị ngưỡng khác nhau và vẽ biểu đồ để dễ dàng quan sát TPR so với FPR. Ví dụ dưới đây là một đường cong ROC
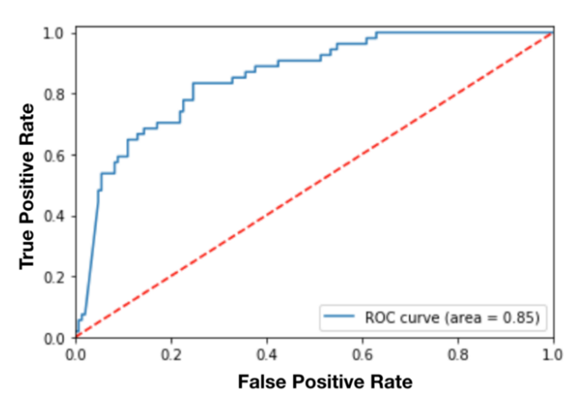
AUC là chỉ số được tính toán dựa trên đường cong ROC nhằm đánh giá khả năng phân loại của mô hình tốt như thê nào. Phần diện tích nằm dưới đường cong ROC và trên trục hoành chính là AUC, có giá trị nằm trong khoảng [0, 1].
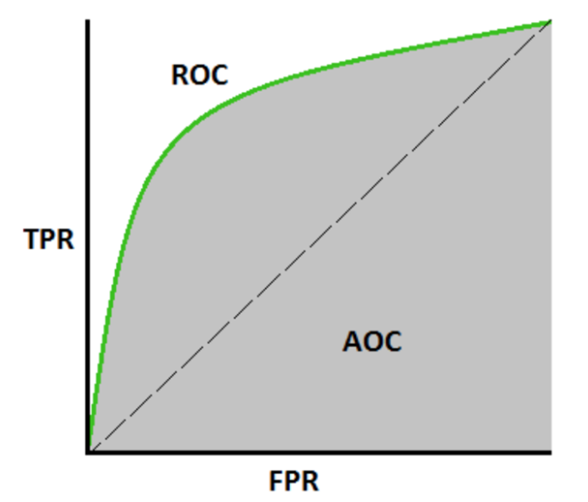
Khi diện tích này càng lớn, đường cong này sẽ dần tiệm cận với đường thẳng y=1 tương đương với khả năng phân loại của mô hình càng tốt. Còn khi đường cong ROC nằm sát với đường chéo đi qua hai điểm (0, 0) và (1, 1), mô hình sẽ tương đương với một phân loại ngẫu nhiên.
Bài toán hồi quy (Regression)
Mô hình hồi quy (Regerssion model) được sử dụng để dự đoán các giá trị mục tiêu là giá tị liên tục. Mô hình này cũng có tính ứng dụng vô cùng rộng, từ bài toán dự đoán giá nhà, hệ thống định giá thương mại điện tử, dự báo thời tiết, dự đoán thị trường chứng khoán, cho đến chuyển hóa độ phân giải hình ảnh siêu cao, tính năng học tập thông qua bộ mã hóa tự động, nén hình ảnh
Một vài mô hình hồi quy phổ biến có thể kể tới như hồi quy tuyến tính (Linear Regression), Random Forest, Convolution neural netwok (tùy vào bài toán mà CNN sẽ phục vụ, CNN có thể đáp ứng cả bài toán phân loại cũng như hồi quy), …
Các metrics được sử dụng để đánh giá mô hình hồi quy phải có khả năng làm việc với tập các giá trị liên tục, và mình xin giới thiệu một số metrics phổ biến sau:
MSE
MSE (Mean Square Error) có lẽ là một metric phổ biến nhất trong các bài toán hồi quy. Về cơ bản, nó tính trung bình của bình phương sai số giữa giá trị thực tế và giá trị dự đoán
Giả sử ta có một bài toán mà chắc hẳn ai đọc về Machine Learning cũng từng đọc qua, chính là bài toán dự đoán giá nhà. Coi giá trị thực tế của nhà thứ i là yi, còn giá trị dự đoán của căn nhà đó là yi’. Vậy, MSE có thể được tính như sau:
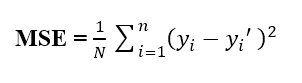
MAE
MAE (Mean Absolute Error) là 1 metric đánh giá mô hình bằng cách tính trung bình giá trị tuyệt đối sai số giữa giá trị thực tế và giá trị dự đoán. Công thức MAE được định nghĩa như sau:
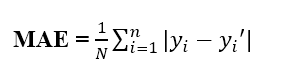
MAE được biết đến là mạnh mẽ hơn đối với các yếu tố ngoại lai (outliers) so với MSE. Lý do chính bởi vì MSE sử dụng bình phương lỗi, các ngoại lai (những samples mà có lỗi cao hơn hẳn các samples khác) sẽ được chú ý và chiếm ưu thế hơn (do tính bình phương) trong việc đánh giá và điều này tác động đến các thông số của mô hình.
Inlier Ratio Metric
Ngoài ra còn có một metric khác dùng để đánh giá các mô hình hồi quy, được gọi là tỷ lệ Inlier. Metric này mình thấy cũng không có nhiều bài báo khoa học dùng, về cơ bản là tính tỷ lệ phần trăm các điểm dữ liệu được dự đoán có lỗi nhỏ hơn biên. Số liệu này chủ yếu được sử dụng trong mô hình RANSAC4 và các phần mở rộng của nó. Các bạn có thể tham khảo thêm tại đây
Bài toán xếp hạng (Ranking)
Ranking được coi là một vấn đề cơ bản trong Machine Learning, nó xếp hạng một danh sách các mục dựa vào sự liên quan giữa chúng trong các bài toán cụ thể (ví dụ như xếp hạng các pages trên Google dựa vào sự liên quan với câu truy vấn tìm kiếm). Theo mình tìm hiểu được, Ranking được ứng dụng rộng rãi trong thương mại điện tử (E-commerce) và các công cụ tìm kiếm (search engines), cụ thể:
- Gợi ý phim ảnh (Netflix, Youtube)
- Xếp hạng page của Google
- Xếp hạng sản phẩm thương mại điện tử (Amazon)
- Tự động hoàn thiện câu truy vấn
- Tìm kiếm hình ảnh (vimeo)
- Tìm kiếm nhà nghỉ (Expedia/Booking)
Trong bài toán Ranking, mo hình cố gắng dự đoán thứ hạng (hoặc chỉ số liên quan) của một danh sách các mục đối với task cụ thể. Thuật toán đối với Ranking có thể chia làm các nhóm sau:
- Point-wise models: Dự đoán một điểm số đối với từng cặp truy vấn-văn bản trong dataset, và sử dụng nó để xếp hạng các mục
- Pair-wise models: Học một phân loại nhị phân mà có thể trả lời rằng văn bản này có liên quan tới truy vấn này hay không?
- List-wise models: Tối ưu hóa trực tiếp giá trị của một trong các thước đô đánh giá, được tính trung bình trên tất cả các truy vấn (Đoạn này hơi khó hiểu chút, bạn có thể tham khảo thêm tại đây
Trong quá trình đánh giá, dự trên thức tự thực của danh sách các mục cho một số truy vấn, chúng ta muốn biết việc dự đoán các mục đó tốt như thế nào. Có khá nhiều metrics được đề xuất như MRR, Precision@K, DCG&NDCG, MAP, Kendall’s tau, … tuy nhiên mình sẽ tập trung vào 3 metrics sau:
MRR
Mean Reciprocal Rank (MRR) là một trong những metrics đơn giản nhất trong việc đánh giá các ranking models. MRR tính trung bình của các thức hạng tương ứng của mục liên quan đầu tiên đối với tập các truy vấn Q, có thể địn nghĩa nó như sau
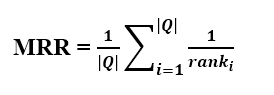
Ví dụ, ta có bảng sau, tương ứng với các queries 1,2,3 sẽ có danh sách dự đoán và đáp án đúng

Vậy MRR = 1/3 * (1/2 + 1/1 + 1/3) = 11/18
Một trong những hạn chế của MRR là nó chỉ tính đến thứ hạng của một trong các mục (mục có liên quan nhất, như ở query 2, chỉ quan tâm tới dự đoán d đầu tiên) và bỏ qua mục khác.
Precision at k
Precision@k : số tài liệu thật sự liên quan đến truy vấn trong k tài liệu có dự đoán liên quan cao nhất

Để mình ví dụ hơn cho dễ hiểu nhé, bạn tìm kiếm từ khóa “Phim Mỹ”, và trong trang đầu tiến, có 8 trên 10 phim gợi ý bạn là phim Mỹ, vậy Precision@10 đối với truy vấn này là 8/10 = 0.8
Khái quát hóa, để tính Precision@k của tập các truy vấn Q, bạn có thể tính bằng cách lấy trung bình của các giá trị Precision@k của các queries trong Q
Hạn chế của Precision@k đó là nó không tốt đối với việc tính đến vị trị các tài liệu liên quan bởi nó chỉ tính số lượng
DCG – NDCG
Normalized Discounted Cumulative Gain (NDCG) có lẽ là metric được được dung phổ biến nhất trong các bài toán learning to rank. Trái ngược với các metrics trước đó, NDCG xem xét thứ tự và sự liên quan quan trọng của các tài liệu, đồng thời chú trọng việc đưa ra các tài liệu có liên quan cao và danh sách được đề xuất
Nghe khá là khó hiểu nhỉ? Trước khi tìm hiểu kĩ hơn về NDCG, cùng nhau tìm hiểu 2 metrics liên quan là Cumulative Gain (CG) và Discounted Cumulative Gain (DCG) nào!
Cumulative Gain (CG) của một tập các tài liệu được truy xuất là tổng các điểm liên quan (relevance score) của chúng đối với câu truy vấn, được định nghĩa như sau:
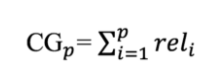
Discounted Cumulative Gain (DCG) là phiên bản có trọng số của CG, sử dụng logarit để giảm relevance score tương ứng với vị trí của các kết quả. Điều này hữu ích với việc muốn ưu tiên cao hơn cho một vài mục tiêu đầu tiến sau khi phân tích hiệu suất của một hệ thống
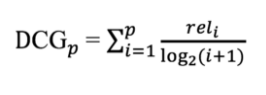
DCG dựa trên giả định sau:
- Các tài liệu có liên quan cao sẽ hưu ích hơn nếu xuất hiện sớm hơn trong kết quả tìm kiếm
- Các tài liệu có liên quan cao sẽ hữu ích hơn các tài liệu có liên quan bên lề tốt hơn các tài liệu không liên quan
Normalized Discounted Cumulative Gain (NDCG) cố gắng nâng cao DCG để phù hợp hơn với các ứng dụng thực tế. Bởi tập hợp các mục được truy xuất có thể khác nhau về kích thước giữa các truy vấn hay hệ thống, NDCG cố gắng so sánh hiệu suất bằng các sử dụng phiên bản chuẩn hóa của DCG. Nói cách khác, nó sắp xếp các tài liệu của 1 danh sách kết quả theo mức độ liên quan, tìm vị trí p có DCG cao nhất, và sử dụng để chuẩn hóa DCG như sau:
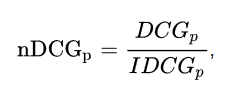
Trong đó, IDCG (Ideal Discounted Cumulative Gain), được định nghĩa như sau:
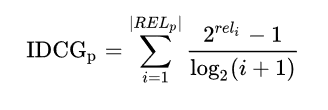
NDCG là một metric khá phổ biến, tuy nhiên cũng có một số hạn chế nhất định. Một trong những hạn chế chính của nó là nó không bắt được các “bad documents” trong kết quả. Nó có thể không phù hợp để đo lường hiệu xuất của các truy vấn mà thường có một số kết quả tốt ngang nhau.
Lời kết
Trên đây là một số metrics đánh giá ứng với các bài toán Machine Learning điển hình mà mình nghĩ các bạn sẽ cần. Đây chưa phải là tất cả nhưng mình thấy khá phổ biến nên đã tìm hiểu và viết bài chia sẻ cho mọi người. Mong là bài viết giúp ích được cho mọi người trên con đường chinh phục Machine Learning. Cảm ơn các bạn đã đọc! Rất mong nhận được những đóng góp cũng như các vấn đề mọi người quan tâm để mình có thể viết thêm bài chia sẻ!
Tài liệu tham khảo
20 Popular Machine Learning Metrics
All rights reserved
