I. Giới thiệu chung

Trie là một cấu trúc dữ liệu dạng cây, hay còn gọi là Cây tiền tố (Suffix tree). Đây là một cấu trúc dữ liệu hữu ích sử dụng để quản lý một tập hợp các xâu kí tự, và có thể mở rộng ra các bài toán liên quan tới quản lý tập số nguyên (xem phần 2 của bài viết tại đây).

Cấu trúc của Trie rất đơn giản, nó là một cây kiểm soát các kí tự của một xâu trên từng cạnh, cho phép lưu trữ các xâu có tiền tố giống nhau rất hiệu quả.

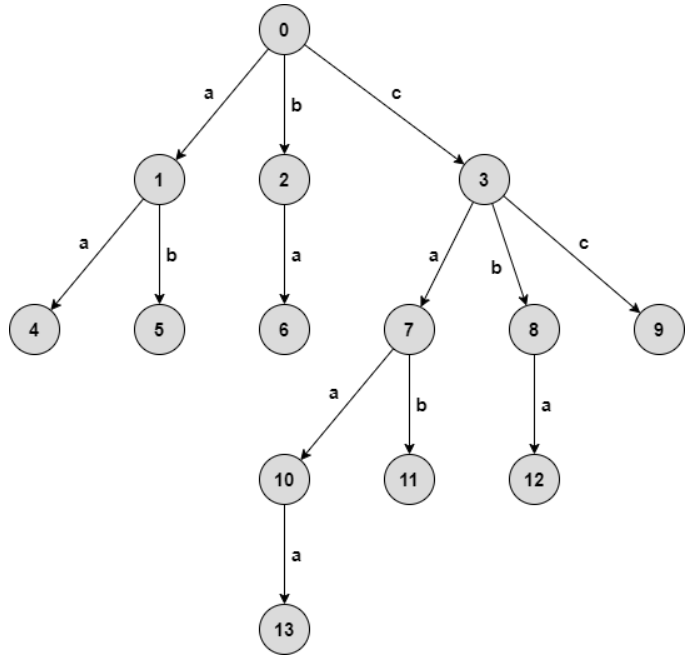
Trên Trie Tree, mỗi đường đi từ gốc tới lá sẽ biểu thị một xâu được tạo thành bởi các kí tự trên các cạnh của đường đi đó. Những xâu có chung tiền tố sẽ có chung một phần đường đi trên cây, chẳng hạn như trong hình vẽ trên, đường đi từ đỉnh $0$ tới đỉnh $13$ biểu thị xâu caaa, còn đường đi từ đỉnh $0$ tới đỉnh $12$ biểu thị xâu cba.

Để cài đặt được Trie Tree, ta chỉ cần xây dựng một cấu trúc $child(u, c) = v$ với ý nghĩa: Nút con của $u$ là $v$ và cạnh giữa chúng biểu diễn kí tự $c,$ hoặc $v = -1$ nếu như $u$ là nút lá. Ví dụ trong hình vẽ trên: child(0, b) = 2, child(3, a) = 7,... Như vậy ta chỉ cần duy trì một mảng $child[26]$ với mỗi đỉnh $u$ để biểu diễn Trie, và xâu tạo thành từ các cạnh trên đường đi từ đỉnh gốc tới đỉnh $u$ sẽ gọi là xâu thể hiện bởi đỉnh $u$.

II. Cài đặt Trie và ứng dụng

1. Phương pháp

Với mục đích giải quyết tốt các bài tập, Trie được cài đặt để hỗ trợ $3$ thao tác sau với độ phức tạp tuyến tính

• Thêm xâu vào tập hợp.
• Xóa một xâu khỏi tập hợp.
• Kiểm tra một xâu có nằm trong tập hợp hay không?

Do vậy, ngoài mảng $child,$ ta cần sử dụng thêm hai biến (tùy vào bài toán có thể bỏ đi):

• $exist$: Có bao nhiêu xâu là xâu được thể hiện bởi đỉnh $u$.
• $cnt$: Có bao nhiêu xâu có tiền tố là xâu được thể hiện bởi đỉnh $u$.

Tức là một đỉnh của cây giờ có dạng $\big(child[26], exist, cnt\big)$. Sau đây ta sẽ nghiên cứu cách cài đặt các thao tác của Trie.

Thao tác thêm xâu

Bắt đầu từ đỉnh gốc, ta duyệt lần lượt qua các kí tự trong xâu và đi xuống cạnh chứa kí tự tương ứng. Nếu như cạnh tương ứng đó chưa tồn tại thì ta tạo đỉnh mới rồi thêm nó vào mảng $child$. Dưới đây là hình ảnh minh họa Trie với tập hợp các xâu aa, aba, ba, caaa, cab, cba, ca.

<center>

Hình ảnh minh họa tham khảo từ VNOI

</center>

Thao tác xóa xâu

Đầu tiên ta kiểm tra xem xâu cần xóa có tồn tại trong Trie hay không, nếu có nhiều xâu như vậy, ta giảm giá trị $exist$ của đỉnh tương ứng với xâu đó đi $1$ đơn vị. Nếu không, ta sẽ đệ quy từ dưới lên trên để xóa các đỉnh dư thừa.

Thao tác tìm xâu

Gần giống với thao tác thêm xâu, chỉ khác là nếu không có cạnh tương ứng với kí tự đang duyệt, ta dừng ngay lập tức vì xâu đó sẽ không thể xuất hiện trong Trie. Sau khi duyệt xong ta kiểm tra ở đỉnh đó có xâu nào kết thúc hay không (tức là kiểm tra $exist \ne 0$).

2. Kĩ thuật cài đặt

Có hai cách cài đặt Trie là cài đặt bằng mảng hoặc cài đặt bằng con trỏ (hay còn gọi là Trie động). Dưới đây tôi sẽ trình bày cả hai cách, tuy nhiên lời khuyên là các bạn nên cài đặt bằng con trỏ, bởi vì ba lí do dưới đây:

• Không cần tính toán bộ nhớ mảng, tránh lãng phí dữ liệu.
• Dễ dàng cài đặt nhiều Trie một lúc bằng cách tạo một gốc mới khi cần một Trie mới.
• Có thể xóa một nút không cần thiết nữa trên Trie.

Các cài đặt trong bài viết này được tham khảo từ trang web VNOI, chỉ chỉnh sửa lại format code một chút nhằm dễ nhìn hơn.

Cài đặt bằng mảng

const int max_nodes = ...;

struct Trie
{
    struct Node
    {
        int child[26];
        int exist, cnt;
    } nodes[max_nodes];

    int cur = 0; // Hiện trong trie đang có bao nhiêu đỉnh.
    
    // Tạo nút gốc cho Trie là đỉnh 0 khi khởi tạo Trie.
    Trie() : cur(0) 
    {   
        memset(nodes[0].child, -1, sizeof(nodes[cur].child));
        nodes[0].exist = nodes[0].cnt = 0;
    };
    
    // Tạo và trả về giá trị của đỉnh mới được tạo ra.
    int new_node() 
    { 
        ++cur;
        memset(nodes[cur].child, -1, sizeof(nodes[cur].child));
        nodes[cur].exist = nodes[cur].cnt = 0;
        
        return cur;
    }

    void add_string(string s) 
    {
        int pos = 0;
        for (auto f : s) 
        {
            int c = f - 'a';
            // Nếu cạnh tương ứng chữ cái c chưa tồn tại thì ta tạo ra đỉnh mới.
            if (nodes[pos].child[c] == -1)
                nodes[pos].child[c] = new_node();
            
            // Có thêm một xâu trong trie có tiền tố là xâu được thể hiện 
            // bằng đỉnh hiện tại.
            pos = nodes[pos].child[c];
            ++nodes[pos].cnt; 
        }
        
        // Đã tìm được đỉnh tương ứng với xâu s, ta tăng biến exist của đỉnh lên 1.
        ++nodes[pos].exist; 
    }
    
    // Trả về liệu đỉnh pos có thể bị xóa đi hay không, đồng thời xóa xâu s nếu có thể. 
    bool delete_string_recursive(int pos, string& s, int i) 
    { 
        // Nếu chưa đến đỉnh tương ứng với xâu s thì tiếp tục đệ quy xuống dưới.
        if (i != (int) s.size()) 
        { 
            int c = s[i] - 'a';
            bool is_child_deleted = delete_string_recursive(nodes[pos].child[c], s, i + 1);
            // Nếu đỉnh con tương ứng bị xóa thì ta gán lại đỉnh tương ứng bằng -1.
            if (is_child_deleted)
                nodes[pos].child[c] = -1;
        }
        // Nếu đã đến đỉnh tương ứng với xâu s thì ta giảm biến exist của đỉnh đi 1
        else 
            --nodes[pos].exist; 
        
        // Nếu đỉnh đang xét không phải gốc thì ta giảm biến cnt của đỉnh đi 1
        // và kiểm tra đỉnh có bị xóa đi hay không?
        // Đỉnh bị xóa nếu không còn xâu nào đi qua nó, nói cách khác là
        // không còn xâu nào có tiền tố là xâu được thể hiện bởi đỉnh pos.
        if (pos != 0) 
        { 
            --nodes[pos].cnt;
            
            if (nodes[pos].cnt == 0) 
                return true;
        }
        
        return false;
    }

    void delete_string(string s) 
    {
        // Kiểm tra xâu s có trong Trie hay không.
        if (find_string(s) == false) 
            return; 
        
        // Gọi hàm đệ quy xóa xâu s khỏi Trie.
        delete_string_recursive(0, s, 0); 
    }

    // Tìm xâu s trong Trie. 
    bool find_string(string s) 
    {
        int pos = 0;
        for (auto f: s) 
        {
            int c = f - 'a';
            if (nodes[pos].child[c] == -1) 
                return false;
            
            pos = nodes[pos].child[c];
        }
        
        // Kiểm tra có xâu nào kết thúc tại đỉnh này hay không.
        return (nodes[pos].exist != 0); 
    }
};

Cài đặt bằng con trỏ

Mặc dù có nhiều ưu điểm, nhưng cài đặt bằng con trỏ cũng rất dễ gây ra nhầm lẫn nếu các bạn chưa vững kiến thức về cấp phát bộ nhớ động. Vì thế, trước khi quyết định sử dụng con trỏ để cài đặt Trie, hãy xem lại các kiến thức dưới đây:

• Tham chiếu, Địa chỉ ảo và Con trỏ trong C++.
• Hoạt động nâng cao với con trỏ C++.
• Kĩ thuật Cấp phát bộ nhớ động.

Các phần trong code có chức năng tương tự như cách cài đặt bằng mảng nên sẽ không chú thích lại!

struct Trie
{
    struct Node
    {
        Node* child[26];
        int exist, cnt;

        Node() 
        {
            for (int i = 0; i < 26; i++) 
                child[i] = NULL;
            
            exist = cnt = 0;
        }
    };
 
    int cur;
    Node* root;
    Trie() : cur(0)
    {
        root = new Node();
    };
 
    void add_string(string s) 
    {
        Node* p = root;
        for (auto f: s) 
        {
            int c = f - 'a';
            if (p -> child[c] == NULL) 
                p -> child[c] = new Node();

            p = p -> child[c];
            p -> cnt++;
        }
        
        p -> exist++;
    }

    bool delete_string_recursive(Node* p, string& s, int i) 
    {
        if (i != (int) s.size()) 
        {
            int c = s[i] - 'a';
            bool is_child_deleted = delete_string_recursive(p -> child[c], s, i + 1);
            if (is_child_deleted) 
                p->child[c] = NULL;
        }
        else 
            p -> exist--;

        if (p != root) 
        {
            p -> cnt--;
            if (p -> cnt == 0) 
            {
                // Khác với cài đặt bằng mảng, ta có thể thực sự xóa đỉnh này đi.
                delete(p); 
                
                return true;
            }
        }
        return false;
    }
 
    void delete_string(string s) 
    {
        if (find_string(s) == false) 
            return;

        delete_string_recursive(root, s, 0);
    }
 
    bool find_string(string s) 
    {
        Node* p = root;
        for (auto f: s) 
        {
            int c = f - 'a';
            if (p -> child[c] == NULL) 
                return false;
            
            p = p -> child[c];
        }
        
        return (p -> exist != 0);
    }
};

III. Các ứng dụng cơ bản

1. Sắp xếp danh sách các xâu

Thông qua Trie Tree, ta có thể đạt được một thuật toán để sắp xếp một danh sách $n$ xâu theo thứ tự từ điển tăng dần chỉ trong thời gian tuyến tính.

Sau khi xây dựng Trie gồm các xâu trong danh sách, ta sử dụng $\text{DFS}$ để duyệt Trie đó, đi lần lượt các cạnh theo thứ tự chữ cái tăng dần. Duyệt tới một đỉnh tới bất kì, ta sẽ in ra các xâu được thể hiện bởi đỉnh đó nếu có. Dễ thấy ta sẽ lần lượt thu được các xâu trong danh sách theo thứ tự từ điển tăng dần.

void dfs(int pos, string& current_string, vector < string >& res) 
{
    for (int i = 1; i <= nodes[pos].exist; ++i) 
        res.push_back(current_string);

    for (int i = 0; i < 26; ++i) 
        if (nodes[pos].child[i] != -1) 
        {
            current_string += char(i + 'a');
            dfs(nodes[pos].child[i], current_string, res);
            current_string.pop_back();
        }
}

vector < string > sort_strings() 
{
    string current_string = "";
    vector < string > res;
    dfs(0, current_string, res);
    
    return res;
}

Độ phức tạp trung bình của cách làm này sẽ là $O(m \times n)$ với $m$ là độ dài trung bình của các xâu. Như vậy, nếu độ dài các xâu nhỏ và danh sách lại gồm nhiều xâu thì cách làm này sẽ có ưu thế hơn so với những thuật toán sắp xếp truyền thống Quicksort hay Mergesort. Và điều quan trọng là Trie có thể hỗ trợ cả các thao tác thêm - xóa - tìm kiếm xâu chỉ trong $O(m),$ nên tùy vào yêu cầu bài toán ta có thể lựa chọn cách tiếp cận phù hợp.

2. Truy vấn tiền tố chung dài nhất của hai xâu

Với một danh sách $n$ xâu, Trie Tree có thể hỗ trợ trả lời truy vấn tìm độ dài tiền tố chung dài nhất giữa hai xâu bất kì trong danh sách.

Đầu tiên, ta thêm tất cả các xâu trong danh sách vào Trie.

Với hai xâu bất kì trong danh sách, ta có thể thấy tiền tố chung của chúng cũng có thể được thể hiện bằng một đỉnh trong Trie. Tìm tiền tố chung dài nhất nghĩa là đi tìm một đỉnh mà từ vị trí đó, hai xâu bắt đầu tách ra hai nhánh khác nhau (khoảng cách tới gốc xa nhất). Dễ nhận thấy, đỉnh biểu thị tiền tố chung dài nhất của hai xâu chính là Nút cha chung gần nhất của hai đỉnh này. Từ đây ta có thể đưa về bài toán LCA trên cây.

Lời giải bài toán LCA các bạn hãy tham khảo lại tại đây.

Code mẫu

#include <bits/stdc++.h>

using namespace std;

struct Trie 
{
    struct Node 
    {
        Node* child[26];
        int index;
        Node () 
        {
            for (int i = 0; i < 26; ++i) 
                child[i] = NULL;

            index = 0;
        }
    };

    Node* root;
    vector < vector < int > > f;
    vector < int > lv;
    vector < int > leaf;
    int max_log;
    int cnt;

    Trie () {}

    Trie(int total_node) 
    {
        root = new Node();
        f.resize(total_node + 5);
        lv.assign(total_node + 5, 0);
        leaf.assign(total_node + 5, 0);
        max_log = log2(total_node + 1);

        for (int i = 0; i <= total_node; ++i)
            f[i].assign(max_log + 1,0);
        
        cnt = 0;
    }

    void add(string s, int id) 
    {
        Node* tmp = root;
        for (int i = 0; i < (int) s.size(); ++i) 
        {
            int c = s[i] - 'a';
            if (tmp -> child[c] == NULL) 
            {
                tmp -> child[c] = new Node();
                tmp -> child[c] -> index = ++cnt;
                f[cnt][0] = (tmp -> index);
                lv[cnt] = i+1;
                for (int j = 1; j <= max_log; ++j) 
                    f[cnt][j] = f[f[cnt][j - 1]][j - 1];
            }

            tmp = tmp -> child[c];
        }

        leaf[id] = cnt;
    }

    int lca (int u, int v) 
    {
        if (lv[u] < lv[v]) 
            swap(u, v);

        for (int j = max_log; j >= 0; --j)
            if (lv[f[u][j]] >= lv[v]) 
                u = f[u][j];
        
        for (int j = max_log; j >= 0; --j) 
            if (f[u][j] != f[v][j]) 
            {
                u = f[u][j];
                v = f[v][j];
            }
        
        while (u != v) 
        {
            u = f[u][0];
            v = f[v][0];
        }

        return u;
    }

    int max_pref(int u, int v) 
    {
        return lv[lca(leaf[u], leaf[v])];
    }
} Tree;


signed main() 
{
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);

    int q; 
    cin >> q;

    int cnt = 0;
    Tree = Trie(5e4);

    while (q--) 
    {
        int t; 
        cin >> t;
        if (t == 1) 
        {
            string s; 
            cin >> s;

            Tree.add(s,++cnt);
        }
        else 
        {
            int u, v; 
            cin >> u >> v;

            cout << Tree.max_pref(u, v) << endl;
        }
    }

    return 0;
}

3. Truy vấn tìm xâu có thứ tự từ điển thứ k

Trong một danh sách gồm $n$ xâu, Trie Tree có thể hỗ trợ truy vấn tìm xâu có thứ tự từ điển lớn thứ $k$ với ý tưởng xây dựng xâu đáp án lần lượt từng kí tự từ trái qua phải.

Đầu tiên ta dựng Trie chứa tất cả các xâu trong danh sách ban đầu. Xuất phát từ đỉnh gốc, ở đỉnh hiện tại đang xét, ta sử dụng biến đếm $cnt$ ở mỗi đỉnh con để xác định kí tự tiếp theo của xâu đáp án là gì. Sau đó di chuyển xuống đỉnh con đó để tiếp tục tìm kí tự tiếp theo.

Code mẫu

string find_kth_string(int k) 
{
    int pos = 0;
    string res = "";
    while (true) 
    {
        if (nodes[pos].exist >= k) 
            break;
        
        k -= nodes[pos].exist;

        for (int i = 0; i < 26; i++) 
            if (nodes[pos].child[i] != -1) 
            {
                int nxt = nodes[pos].child[i];
                if (nodes[nxt].cnt >= k) 
                {
                    res += char(i + 'a');
                    pos = nxt;
                    break;
                }
                
                k -= nodes[nxt].cnt;
            } 
    }

    return res;
}

IV. Một số bài tập khác

1. FSTR

Đề bài

Bờm viết một chương trình hỗ trợ học ngoại ngữ. Module quản lí từ vựng với phép tìm kiếm từ được Bờm xây dựng theo quy trình: Giả sử danh sách từ chương trình đang có là $w_1, w_2,..., w_N,$ mỗi khi nhận được mẫu tìm kiếm $P,$ chương trình sẽ lần lượt so sánh $P$ với $w_1, w_2,...$ cho đến khi gặp từ trùng với $P$ hoặc đã hết danh sách từ. Khi so sánh $P$ với các từ, chương trình sẽ lần lượt so sánh các kí tự từ trái qua phải cho đến khi gặp kí tự sai khác hay một trong hai từ kết thúc (khi đó nếu cả hai từ cùng kết thúc là tìm kiếm thành công).

Để khảo sát hiệu năng của module tìm kiếm, Bờm xây dựng một danh sách $N$ từ và thực hiện tìm kiếm $Q$ mẫu, với mỗi mẫu Bờm cần xác định số thao tác cơ sở mà chương trình thực hiện, thao tác cơ sở là một lần so sánh kí tự hoặc một lần xử lí khi gặp kết thúc từ. Số thao tác cơ sở thực hiện với mỗi mẫu tìm kiếm sẽ bằng tổng của: Số lượng từ được so sánh với mẫu và độ dài của tiền tố chung dài nhất của mỗi từ với mẫu.

Yêu cầu: Hãy giúp Bờm thực hiện việc khảo sát trên mà không cần thực hiện chương trình của Bờm?

Ý tưởng

Ta xử lý offline các truy vấn.

Với mỗi mẫu tìm kiếm gọi $pos_i$ là vị trí nhỏ nhất sao cho $w_{1...pos_i}$ bằng với mẫu tìm kiếm đó (có thể cài đặt bước này bằng map, chặt nhị phân, Trie Tree,...). Ở đây ta sẽ sử dụng Trie vì mục đích luyện tập.

Sắp xếp lại các mẫu tìm kiếm theo $pos_i$.

Xử dụng hai con trỏ, khi duyệt đến mẫu tìm kiếm thứ $i$ ta thêm dần các $w_j$ với $j \leq pos_i$ vào Trie.

Kết quả của mỗi truy vấn có thể tính thông qua Trie như đoạn code dưới đây:

int find(string s)
{
    int pos = 0, ans = 0;
    for (auto ch : s)
    {
        int i = ch - 'a';

        if (trie[pos].child[i] == -1)
            return 0;

        pos = trie[pos].child[i];
        ans += trie[pos].cnt;
    }

    return ans;
}

Độ phức tạp: $O(n + m),$ với $m$ là tổng độ dài các xâu.

Code mẫu

#include <bits/stdc++.h>
#define int long long

using namespace std;

const int maxn = 30050;
int res[maxn];
string s[maxn], t[maxn];

struct Node 
{
    Node* child[26];
    vector < int > v;
    int cost;

    Node() 
    {
        for (int i = 0; i < 26; ++i)
            child[i] = NULL;

        cost = 0;
    }
};

struct Trie 
{
    Node* root;

    Trie()
    {
        root = new Node();
    }

    void add(string s, int id) 
    {
        Node* p = root;
        for (int i = 0; i < s.size(); ++i) 
        {
            int c = s[i] - 'a';
            if (p -> child[c] == NULL)
                p -> child[c] = new Node();

            p = p -> child[c];
        }

        p -> v.push_back(id);
    }
};

void process(Trie* root, string s) 
{
    Node* p = root -> root;
    int cur = 0;
    for (int i = 0; i < s.size(); ++i) 
    {
        int c = s[i] - 'a';
        p -> cost++;
        cur += p -> cost;

        if (p -> child[c] == NULL) 
            return; 

        p = p -> child[c];
    }

    p -> cost++; 
    cur += p -> cost;

    vector < int > v = p -> v;
    for (int i = 0; i < v.size(); ++i)
        res[v[i]] = cur;

    p -> v.clear();
}

void cal(Node* u, int cost) 
{
    for (int i = 0; i < u -> v.size(); ++i) 
        res[u -> v[i]] = cost;

    for (int i = 0; i < 26; ++i) 
    {
        if (u -> child[i] == NULL) 
            continue;

        cal(u -> child[i], u -> child[i] -> cost + cost);
    }
}

void solution(Trie* root, int n, int q) 
{
    memset(res, 0, sizeof(res));

    for (int i = 1; i <= n; ++i) 
        process(root, s[i]);

    cal(root -> root, root -> root -> cost);

    for (int i = 1; i <= q; ++i) 
        cout << res[i] << '\n'; 
}

signed main() 
{
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);

    int n, q;
    cin >> n >> q;

    for (int i = 1; i <= n; ++i) 
        cin >> s[i];

    Trie* root = new Trie();
    for (int i = 1; i <= q; ++i) 
    {
        cin >> t[i];
        root -> add(t[i], i);
    }

    solution(root, n, q);

    return 0;
}

2. Perfect Matching

Đề bài

Một lớp học nọ có $n$ học sinh, tên của học sinh thứ $i$ được biểu diễn bằng một chuỗi kí tự $s_i$.

Có $n$ biệt danh cũng được biểu diễn bằng các chuỗi kí tự $p_i$.

Ta kí hiệu $lcp(a,b)$ là độ dài tiền tố chung dài nhất giữa hai xâu $a$ và $b$.

Bạn có thể chọn $c$ là dãy hoán vị từ $1$ tới $n,$ tương đương với việc gán cho bạn thứ $i$ biệt danh là $p_{c_i}$. Cách chọn này có độ "hoàn hảo" là $\sum lcp(s_i,p_{c_i}); \forall i \in[1,n]$.

Yêu cầu: Hãy tìm dãy hoán vị $c$ có độ hoàn hảo lớn nhất?

Ý tưởng

Tóm tắt

Cho hai tập xâu $A$ và $B$ đều có $n$ phần tử, tìm cách ghép $n$ cặp xâu $s_i, t_i \ (s \in A, t \in B)$ sao cho tổng $\sum^n_{i = 1}lcp(s_i, t_i)$ là lớn nhất.

Hướng giải

Bài này ta có thể giải bằng cách $\text{DFS}$ trên cây Trie. Đầu tiên, ta cho hết các xâu thuộc tập $A$ và $B$ vào trong cây. Gọi $x$ là nút ta đang thực hiện $\text{DFS},$ $h(x)$ là khoảng cách từ nút gốc đến $x, cnt_A(x), cnt_B(x)$ lần lượt là số xâu thuộc tập $A$ và tập $B$ mà đi qua nút này.

Nhận xét: Khi hai xâu $s, t$ đều đi qua một nút $x$ trong cây Trie, thì $lcp(s, t) \ge h(x)$. Nhận xét này chính từ cách hoạt động của Trie là gộp các xâu có cùng tiền tố.

Từ đây ta có thuật toán tham lam như sau: $\text{DFS}$ từ gốc của Trie, sau đó đi tới nút sâu nhất có thể thỏa mãn có ít nhất một xâu thuộc tập $A$ và một xâu thuộc tập $B,$ sau đó ghép chúng thành $\text{min}\big(cnt_A(x), cnt_B(x)\big)$ cặp có $lcp = h(x)$. Cuối cùng cộng vào nút cha các xâu chưa được ghép cặp để khi kết thúc $\text{DFS}$ ta sẽ quay lại ghép tiếp.

Độ phức tạp: $O(n + m)$.

Code mẫu

#include <bits/stdc++.h>

using namespace std;

// Cấu trúc một Node trên Trie. Ở code này cài riêng ra ngoài chứ không lồng vào Trie, để 
// khi DFS vẫn khai báo được tham số kiểu Node*. 
struct Node
{
    Node* child[26];
    vector < int > v[2]; // v[0] lưu chỉ số của n xâu tên đầu, v[1] lưu chỉ số của n xâu biệt danh sau.

    Node()
    {
        for (int i = 0; i < 26; ++i)
            child[i] = NULL;
    }
};

struct Trie
{
    // Con trỏ trỏ vào Node gốc của 1 Trie khi tạo ra.
    Node* root;

    Trie()
    {
        root = new Node();
    }

    void add(string s, int id, int pos)
    {
        Node* p = root;
        for (int i = 0; i < (int) s.size(); ++i)
        {
            int c = s[i] - 'a';
            if (p -> child[c] == NULL)
                p -> child[c] = new Node();

            p = p -> child[c];
        }

        p -> v[pos].push_back(id);
    }
};

int res = 0;

void dfs(Node* u, int depth)
{
    for (int i = 0; i < 26; ++i)
    {
        if (u -> child[i] == NULL)
            continue;

        dfs(u -> child[i], depth + 1);

        vector < int > cop = u -> child[i] -> v[0];
        for (int i = 0; i < (int) cop.size(); ++i)
            u -> v[0].push_back(cop[i]);

        cop = u -> child[i] -> v[1];
        for (int i = 0; i < (int) cop.size(); ++i)
            u -> v[1].push_back(cop[i]);
    }

    res += depth * min(u -> v[0].size(), u -> v[1].size());

    while (u -> v[0].size() && u -> v[1].size())
    {
        u -> v[0].pop_back();
        u -> v[1].pop_back();
    }
}

int main()
{
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);

    int n;
    cin >> n;

    Trie* root = new Trie();
    for (int i = 1; i <= n; ++i)
    {
        string s;
        cin >> s;
        root -> add(s, i, 0);
    }

    for (int i = 1; i <= n; ++i)
    {
        string s;
        cin >> s;

        root -> add(s, i, 1);
    }

    dfs(root -> root, 0);

    cout << res;
}

V. Tài liệu tham khảo

• https://vnoi.info/wiki/algo/data-structures/trie.md
• https://leduythuccs.github.io/2018-05-23-c-u-tr-c-d-li-u-trie/

Để tiếp tục xem phần thứ $2$ của bài viết, mời các bạn nhấn vào đây.