Đây là bài viết số $2$ thuộc series bài viết về cấu trúc dữ liệu Trie Tree. Để hiểu được bài viết này, trước tiên các bạn hãy tìm đọc lại bài viết phần $1$ liên quan tới Trie Tree cơ bản tại đây: Trie Tree phần 1.

I. Giới thiệu chung

Ta đã biết rằng Trie là một cấu trúc dữ liệu dạng cây, sử dụng rất hiệu quả trong các bài toán liên quan tới quản lý danh sách xâu kí tự. Tuy nhiên, ít ai biết rằng Trie Tree còn có một ứng dụng nữa, đó là quản lý một tập số nguyên.

Bằng cách coi mỗi số là một xâu kí tự gồm toàn kí tự 0 và 1 (tức là biểu diễn nhị phân của số đó), ta có thể quản lý tập hợp số này cùng với những thao tác hỗ trợ để xử lý những bài toán về số nguyên.

Dưới đây là một ví dụ minh họa về Trie nhị phân quản lý tập các số nguyên $\{0, 1, 2, 4, 6\}$.

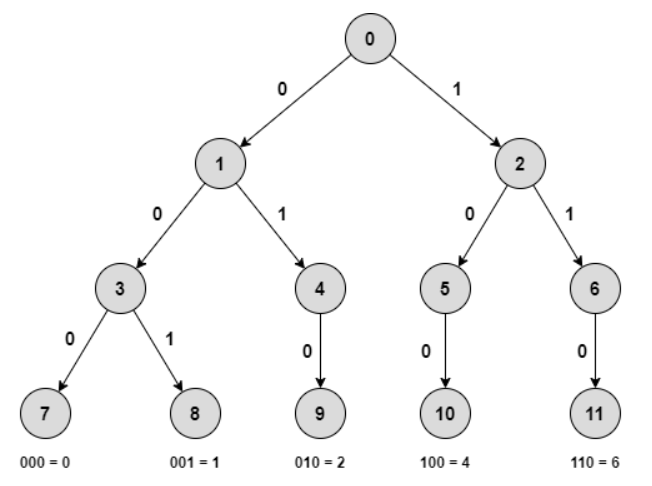
Trie nhị phân có một số đặc điểm sau:

• Các số được thêm vào Trie sẽ được chuyển qua dạng nhị phân, rồi thêm các bit $0$ vào đầu sao cho độ dài của chúng đều bằng nhau. Thông thường độ dài này sẽ được đặt là $\log\big(\text{max}(a_i)\big)$ với $a_i$ là các số trong tập hợp.
• Một số nguyên sẽ bao gồm các bit trên đường đi từ nút gốc tới nút lá của Trie Tree (mỗi cạnh lưu một bit).
• Khi thêm các bit vào Trie, ta thêm theo chiều từ trái sang phải.

II. Cài đặt và ứng dụng

1. Cài đặt

Các ứng dụng của Trie trên xâu đều có thể áp dụng trên Trie nhị phân. Các thao tác cơ bản trên Trie nhị phân bao gồm:

• Thêm một nút trên Trie.
• Thêm một số vào Trie.
• Xóa một số khỏi Trie.
• Kiểm tra một số có xuất hiện trong Trie hay không.

Và dĩ nhiên, ta cũng có thể sử dụng một trong hai cách cài đặt bằng mảng hoặc bằng con trỏ.

Cài đặt bằng mảng

const int MAX_NODES = ...;
const int LOG = ...; // Giá trị lớn nhất của log(a[i]).

struct Trie
{
    struct Node
    {
        int child[2];
        int exist, cnt;
    } nodes[MAX_NODES];
    
    // Số lượng node hiện tại của Trie.
    int cur;
    
    Trie() : cur(0) 
    {
        memset(nodes[0].child, -1, sizeof(nodes[cur].child));
        nodes[0].exist = nodes[0].cnt = 0;
    };

    int new_node() 
    {
        ++cur;
        memset(nodes[cur].child, -1, sizeof(nodes[cur].child));
        nodes[cur].exist = nodes[cur].cnt = 0;
        
        return cur;
    }

    void add_number(int x) 
    {
        int pos = 0;
        for (int i = LOG; i >= 0; --i) 
        {
            int c = (x >> i) & 1;
            if (nodes[pos].child[c] == -1) 
                nodes[pos].child[c] = new_node();
            pos = nodes[pos].child[c];
            ++nodes[pos].cnt;
        }
        
        ++nodes[pos].exist;
    }

    void delete_number(int x) 
    {
        if (find_number(x) == false) 
            return;
        
        int pos = 0;
        for (int i = LOG; i >= 0; --i) 
        {
            int c = (x >> i) & 1;
            int tmp = nodes[pos].child[c];
            nodes[tmp].cnt--;
            
            if (nodes[tmp].cnt == 0) 
            {
                nodes[pos].child[c] = -1;
                return;
            }

            pos = tmp;
        }
        
        --nodes[pos].exist;
    }

    bool find_number(int x) 
    {
        int pos = 0;
        for (int i = LG; i >= 0; --i) 
        {
            int c = (x & (1 << i) ? 1 : 0);
            
            if (nodes[pos].child[c] == -1) 
                return false;
            
            pos = nodes[pos].child[c];
        }
        
        return (nodes[pos].exist != 0);
    }
};

Cài đặt bằng con trỏ

const int LOG = ...; // Giá trị lớn nhất của log(a[i]).
    
struct Trie
{
    struct Node
    {
        Node* child[2];
        int exist, cnt;

        Node() 
        {
            for (int i = 0; i < 2; ++i) 
                child[i] = NULL;
            
            exist = cnt = 0;
        }
    };
 
    Node* root;
    Trie() : cur(0)
    {
        root = new Node();
    };
 
     void add_number(int x) 
     {
        Node* p = root;
         
        for (int i = LOG; i >= 0; --i) 
        {
            int c = (x >> i) & 1;
            if (p -> child[c] == -1) 
                p -> child[c] = new Node();
            
            p = p -> child[c];
            p -> cnt++;
        }
         
        p -> exist++;
    }

    void delete_number(int x) 
    {
        if (find_number(x) == false) 
            return;
        
        Node* p = root;
        for (int i = LOG; i >= 0; --i) 
        {
            int c = (x >> i) & 1;
            Node* tmp = p -> child[c];
            tmp -> cnt--;
            
            if (tmp -> cnt == 0) 
            {
                p -> child[c] = -1;
                return;
            }

            p = tmp;
        }
        
        p -> exist--;
    }

    bool find_number(int x) 
    {        
        Node* p = root;
        for (int i = LOG; i >= 0; --i)  
        {
            int c = (x & (1 << i) ? 1 : 0);
            
            if (p -> child[c] == NULL) 
                return false;
            
            p = p -> child[c];
        }
        
        return (p -> exist != 0);
    }
};

2. Xử lí truy vấn tìm XOR lớn nhất với giá trị được cho

Đây là một bài toán điển hình sử dụng trie nhị phân. Đa số các bài toán liên quan tới thao tác bit sử dụng trie đều là biến thể của bài toán này.

Đề bài

Cho $n$ số nguyên không âm $a_1, a_2, \dots, a_n$ và $m$ truy vấn, mỗi truy vấn yêu cầu tìm giá trị:

$$\text{max}_{i = 1}^n\big(a_i \oplus x\big)$$

<center>

với $x$ là một số nguyên không âm cho trước, $\oplus$ là toán tử $\text{XOR}$ bit

</center>

Yêu cầu: Xử lý tất cả các truy vấn?

Ý tưởng

Đầu tiên xây dựng một Trie nhị phân với các số nguyên đã cho.

Xét lần lượt các bit từ lớn đến bé của đáp án. Coi bit đang xét là bit thứ $i$. Ta sẽ xây dựng đáp án một cách tham lam bằng cách cố gắng đặt bit thứ $i$ của đáp án là $1$ do $2^i > \sum_{i = 0}^{j - 1} 2^j$. Nói cách khác, dù đặt cả $i − 1$ bit còn lại của đáp án là $1$ thì cũng không có lợi bằng đặt bit $i$ là $1$.

Ta sẽ lần lượt xây đáp án bằng các đi xuống từ gốc của Trie. Giả sử ta đang xây dựng bit thứ $i$ của đáp án. Nếu đỉnh hiện tại đang xét có thể đi xuống cạnh có bit là $f(x,i) \oplus 1$ với $f(x,i)$ là bit thứ $i$ của số $x,$ ta sẽ đi qua cạnh đó để có được bit $i$ trong đáp án là $1$. Nếu không, ta "đành" đi xuống cạnh còn lại của đỉnh đang xét và có được bit $i$ của đáp án là $0$.

Cài đặt

// Cài đặt bằng con trỏ, chỉ cần thêm hàm này vào trong cấu trúc Trie.
int query(int x) 
{
    int res = 0;
    Node* p = root;
    
    for (int i = LOG; i >= 0; --i) 
    {
        int c = (x >> i) & 1;

        if (p -> child[c ^ 1] != -1) 
        {
            res += (1ll << i);
            p = p -> child[c ^ 1];
        }
        else 
            p = p -> child[c];
    }
    
    return res;
}

III. Bài tập áp dụng

1. GCD, XOR & SUM

Đề bài

Tý đang chơi một trò chơi về những con số và nhờ sự thông minh của mình, cậu giữ chuỗi thắng liên tiếp trong nhiều ngày. Một ngày, Tý đi du lịch và không thể tiếp tục chuỗi thắng, vì thế cậu nhờ người bạn Tèo của mình giúp đỡ tiếp tục trò chơi. Trò chơi này như sau:

Ban đầu, có một mảng $A$ rỗng. Máy tính sẽ đưa ra hai loại truy vấn:

• $1 \ u_i$: Thêm số $u_i$ vào mảng $A$.
• $2 \ x_i \ k_i \ s_i$: Tìm số $v$ thuộc mảng $A$ sao cho $\text{GCD}(x_i, v)$ chia hết cho $k_i; x_i + v_i \le s_i$ và $x_i \oplus v$ là lớn nhất có thể (với $oplus$ là toán tử $\text{XOR}$ bit). Nếu không có số $v$ như vậy thì trả về $-1$.

Yêu cầu: Hãy giúp Tèo thực hiện $q$ truy vấn mà máy tính đưa ra?

Input:

• Dòng đầu tiên chứa số nguyên dương $q$ - số lượng truy vấn.
• Trên $q$ dòng tiếp theo, mỗi dòng chứa một trong hai loại truy vấn đã nêu.

Ràng buộc:

• $1 \le q \le 10^5$.
• $1 \le u_i \le 10^5$.
• $1 \le x_i, k_i, s_i \le 10^5$.

Output:

• Với mỗi truy vấn loại $2,$ đưa ra giá trị $v$ tìm được hoặc $-1$ nếu không tìm được (mỗi truy vấn đưa ra kết quả trên một dòng).

Sample Input:

5
1 1
1 2
2 1 1 3
2 1 1 2
2 1 1 1

Sample Output:

2
1
-1

Ý tưởng

Nhìn thấy bài toán tìm $x_i \oplus v$ lớn nhất ngay lập tức gợi cho chúng ta lời giải sử dụng Trie. Vì vậy ta sẽ cố gắng thiết kế Trie để truy vấn trên tập các số thỏa mãn hai điều kiện còn lại.

Để $GCD(x_i, v)$ chia hết cho $k_i,$ dễ nhận thấy cả $x_i$ và $v$ đều phải chia hết cho $k_i$. Do vậy, ta sẽ tạo $10^5$ trie, với Trie thứ $i$ là các số trong mảng $a$ chia hết cho $i$. Để $x_i+v ≤ s_i$ thì dĩ nhiên $v≤s_i−x_i,$ ta lưu với mỗi đỉnh trong Trie số bé nhất trong cây con của đỉnh đó là bao nhiêu.

Vậy để giải quyết một truy vấn, ta sẽ tìm giá trị $\text{XOR}$ lớn nhất trên Trie thứ $k_i$ (cách giải đã trình bày ở trên) và chỉ đi vào một đỉnh con nếu như giá trị bé nhất của cây con đó bé hơn hoặc bằng $s_i−x_i$.

Độ phức tạp: $O(n \times \log + q \times \log^2)$.

Code mẫu

#include <bits/stdc++.h>

using namespace std;

const int LG = 18;
const int INF = 1e9;

struct Trie
{
    struct Node
    {
        Node* child[2];
        int mn;

        Node() 
        {
            for (int i = 0; i < 2; i++) 
                child[i] = NULL;
                
            mn = INF;
        }
    };

    Node* root;
    Trie() : cur(0) 
    {
        root = new Node();
    };

    void add_number(int x) 
    {
        Node* p = root;
        for (int i = LG; i >= 0; i--) 
        {
            int c = (x >> i) & 1;
            if (p -> child[c] == NULL) 
                p -> child[c] = new Node();

            p = p -> child[c];
            p -> mn = min(p -> mn, x);
        }
    }

    int query(int x, int val) 
    {
        Node* p = root;
        int res = 0;
        for (int i = LG; i >= 0; i--) 
        {
            int c = (x >> i) & 1;
            if (p -> child[c ^ 1] != NULL && p -> child[c ^ 1] -> mn <= val) 
            {
                res += ((c ^ 1) << i);
                p = p -> child[c ^ 1];
            }
            else 
            {
                if (p -> child[c] == NULL || p -> child[c] -> mn > val) 
                    return -1;
                
                p = p -> child[c];
                res += (c << i);
            }
        }
        
        return res;
    }
};

const int maxn = 1e5;
Trie tries[maxn + 5];
vector < int > d[maxn + 5];

signed main() 
{
    ios_base::sync_with_stdio(false); 
    cin.tie(nullptr);

    for (int i = 1; i <= N; i++) 
        for (int j = i; j <= N; j += i) 
            d[j].push_back(i);
    
    int q;
    cin >> q;
    
    while (q--) 
    {
        int t;
        cin >> t;

        if (t == 1) 
        {
            int u;
            cin >> u;
            
            for (auto x : d[u]) 
                tries[x].add_number(u); 
        }
        else 
        {
            int x, k, s;
            cin >> x >> k >> s;

            if (x % k != 0) 
                cout << "-1\n";
            else 
                cout << tries[k].query(x, s - x) << "\n";
        }
    }
    
    return 0;
}

2. KXOR

Đề bài

Cho một dãy số nguyên dương $a_1, a_2,..., a_n$.

Yêu cầu: Đếm số cách chia dãy này thành $k$ đoạn con liên tiếp, thỏa mãn tổng $\text{XOR}$ đoạn thứ $i \ (i \le k)$ nằm trong đoạn $[L_i, R_i]?$

Input:

• Dòng thứ nhất gồm hai số nguyên dương $n$ và $k$.
• Dòng thứ hai gồm $n$ số nguyên dương $a_1, a_2,..., a_n$.
• Trên $k$ dòng tiếp theo, mỗi dòng gồm 2 số nguyên dương $L_i$ và $R_i$ là điều kiện của đoạn thứ $i$.

Ràng buộc:

• $1 \le k \le n \le 10^5, n \times k \le 10^5$.
• $a_i \le 10^9; \forall i: 1 \le i \le n$.
• $1 \le L_i \le R_i \le 10^9; \forall i: 1 \le i \le k$.

Output:

• Gồm một số nguyên duy nhất là kết quả của bài toán. Do kết quả có thể khá lớn, hãy in ra phần dư của kết quả sau khi chia cho $10^9 + 7$.

Sample Input:

4 2
1 2 3 4
1 4
2 10

Sample Output:

2

Ý tưởng

Ta định nghĩa:

• $dp[i][j]$ là số cách chia dãy từ $a_{1...i}$ thành $j$ nhóm và những cách chia này thỏa mãn với yêu cầu đề bài.
• $pre[i]$ là tổng xor của dãy $a_{1...i} \ (a_1 \oplus a_2 \oplus ... \oplus a_i)$.
• $mask(x, i)$ là bit thứ $i$ của $x$.

Từ đó ta dễ dàng xây dựng được công thức: $$dp[i][j] = \sum_{\substack k=1}^{i-1} dp[k][j - 1]$$ với điều kiện $L[j] \le pre[i] \oplus pre[k] \le R[j]$.

Giải thích điều kiện:

$$L[j] \le (a_{k+1} \oplus a_{k+2} \oplus ... \oplus a_i) \le R[j] \implies L[j] \le pre[i] \oplus pre[k] \le R[j]$$

Vậy ta sẽ chuyển bài toán về thành: Với mỗi $(i, j),$ cần tính hiệu của (tổng của các $dp[k][j-1]$ với $pre[i] \oplus pre[k] \le R[j] \ (1)$ và tổng của các $dp[k][j - 1]$ với $pre[i] \oplus pre[k] \le L[j] - 1 \ (2)$).

Ta sẽ sử dụng $k$ cây Binary Indexed Trie lưu biến sum, cây Trie thứ $j$ sẽ lưu các số $pre[k]$ và cộng vào biến sum ở các node mà $pre[k]$ đi qua một lượng $dp[k][j]$.

Để tìm tổng $(1),$ ta sẽ xét lần lượt các bit từ lớn đến bé của $R[j]$ và $pre[i],$ đi từ gốc của cây Trie thứ $j,$ xảy ra các trường hợp sau (giả sử đang xét bit thứ $x$):

• $mask\big(R[j], x\big) = 1$: Ta sẽ cộng vào $dp[i][j]$ một lượng $sum$ của của cây con tương ứng với $mask\big(pre[i], x\big)$. Sau đó ta đi xuống cây con tương ứng với $mask\big(R[j], x\big) \oplus mask \big(pre[i], x\big)$.
• $mask\big(R[j], x\big) = 0$: ta đi xuống cây con tương ứng với $mask\big(R[j], x\big) \oplus mask\big(pre[i], x\big)$.

Tổng $(2)$ tìm tương tự giống tổng $(1)$.

Độ phức tạp: $O\big(n \times k \times \log(10^9)\big)$.

Code mẫu

#include <bits/stdc++.h>
#define int long long
#define nd second
#define st first
#define endl "\n"

using namespace std;

const int MOD = 1e9 + 7;
int n, k;
vector < int > a, pre;
vector < vector < int > > dp;
vector < ii > Q;

void add(int& x, int y)
{
    x += y;
    if (x >= MOD)
        x -= MOD;
    if (x < 0)
        x += MOD;
}

struct Trie
{
    Trie* child[2];
    int sum;
};

struct Trie* get_node(void)
{
    Trie* x = new Trie();
    x -> sum = 0;
    return x;
}

vector < Trie* > root;

void insert(int team, int XOR, int val)
{
    Trie* x = root[team];
    for (int i = 30; i >= 0; --i)
    {
        int key = (XOR >> i) & 1;
        if (!x -> child[key]) 
            x -> child[key] = get_node();
        x = x -> child[key];

        add(x -> sum, val);
    }
}

void solution()
{
    for (int i = 1; i <= n; ++i)
    {
        for (int j = 1; j <= min(i, k); ++j)
        {
            int l = Q[j].st - 1, r = Q[j].nd;
            int res = 0;
            Trie* x = root[j - 1];
            int bit;
            for (bit = 30; bit >= 0; bit--)
            {
                int key = (r >> bit) & 1, k = (pre[i] >> bit) & 1;
                if (key && x -> child[k]) 
                    add(res, x -> child[k] -> sum);
                
                if (!x -> child[key ^ k]) 
                    break;

                x = x -> child[key ^ k];    
            }

            if (bit == -1) 
                add(res, x -> sum);
            
            x = root[j - 1];
            if (l >= 0)
            {
                for (bit = 30; bit >= 0; bit--)
                {
                    int key = (l >> bit) & 1, k = (pre[i] >> bit) & 1;
                    if (key && x -> child[k]) 
                        add(res, -x -> child[k] -> sum);
                    
                    if (!x -> child[key ^ k]) 
                        break;

                    x = x -> child[key ^ k];
                }

                if (bit == -1) 
                    add(res, -x -> sum);
            }

            dp[i][j] = res;
        }

        for (int j = 1; j <= min(i, k); ++j)
            insert(j, pre[i], dp[i][j]);
    }

    cout << dp[n][k] << endl;
}

signed main()
{
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);

    cin >> n >> k;

    a.resize(n + 2);
    pre.resize(n + 2);
    dp.resize(n + 2, vector<int>(k + 2));
    Q.resize(k + 2);
    root.resize(k + 2);
    for (int i = 0; i <= k; ++i) 
        root[i] = get_node();

    for (int i = 1; i <= n; ++i) 
        cin >> a[i], pre[i] = pre[i - 1] ^ a[i];
    for (int i = 1; i <= k; ++i) 
        cin >> Q[i].st >> Q[i].nd;
    insert(0, 0, 1);
    
    solution();

    return 0;
}

IV. Tài liệu tham khảo

• https://vnoi.info/wiki/algo/data-structures/trie.md
• https://leduythuccs.github.io/2018-05-23-c-u-tr-c-d-li-u-trie/