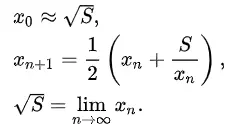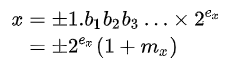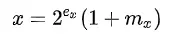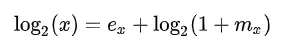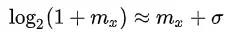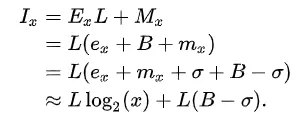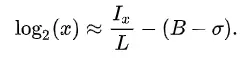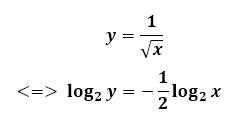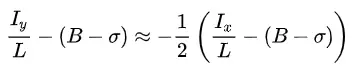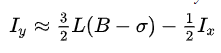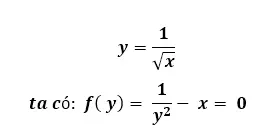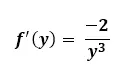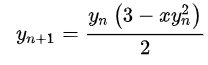Mở đầu

Vào khoảng những năm 2002, 2003, khi mã nguồn của tựa game Quake 3 Arena được chuyển thành mã nguồn mở, người ta đã tìm ra một hàm tính ra được giá trị nghịch đảo của căn bậc 2 một cách nhanh chóng, được biết đến rộng rãi với cái tên Fast inverse square root. Vào thời điểm đó, phép tính căn bậc 2 là một phép tính tốn nhiều tài nguyên, mà lại rất hay được sử dụng trong các phép tính vector. Với một game 3d đột phá vào thời điểm đó như Quake 3, thì sử dụng rất nhiều các phép tính dạng này. Mặc dù John Carmack, cha đẻ của dòng game Quake được nhắc đến như người đưa thuật toán trở nên phổ biến, nhưng những cài đặt đầu tiên đã được Gary Tarolli thực hiện trên máy tính SGI Indigo.

Cách máy tính tính căn bậc 2

Thực sự để tính xấp xỉ căn bậc 2 của một số, có rất nhiều phương pháp. Dựa theo bài viết Methods of computing square roots , ta có thể thấy, các phương pháp trên đều dựa trên việc đưa ra một dãy vô hạn, một công thức truy hồi dẫn đến kết quả của phép tính căn bậc 2. bằng việc lặp lại công thức đến độ chính xác tùy ý, ta có thể đưa ra kết quả với độ chính xác tùy ý.

Mô tả phương pháp Babylon Ví dụ, để tính căn bậc 2 của 125348, ta sẽ tính như sau:

Trên các máy tính hiện đại ngày nay, đã có các bộ chỉ thị phần cứng riêng để thực hiện việc này, bằng nhiều phương pháp khác nhau. Tuy nhiên vào thời điểm thập niên 90 của thế kỉ trước, phương pháp Fast inverse square root là một phương pháp hay, mang lại hiệu quả tính toán mà phần cứng chưa thể cung cấp được.

Cơ sở lý thuyết

Thuật toán được mô tả cơ bản như sau:

1. Chuyển số sang dạng nguyên, tính xấp xỉ -1/2 log2(x)
2. Đổi lại số sang dạng số thực
3. Xấp xỉ 1 lần nữa với phương pháp Newton

Xấp xỉ Log2(x)

Biểu diễn số thực x dưới dạng tích của một số thực với một lũy thừa của 2.

với ex là số tự nhiên lớn hơn 0, mx thuộc đoạn từ 0 đến 1. Xem thêm bài Single-precision floating-point format để hiểu về cách biểu diễn số thực dấu phẩy động trên máy tính. Ta tính được 3 giá trị:

• Sx, là dấu, 0 nếu x > 0, là 1 nếu x < 0 (1 bit)
• Ex = ex + B là "biased exponent", với B = 127 là giá trị "exponent bias"(8 bits)
• Mx = mx × L, với L = 223(23 bits)

Ta có:

Suy ra:

Vì m nằm trong đoạn 0 đến 1, ta có:

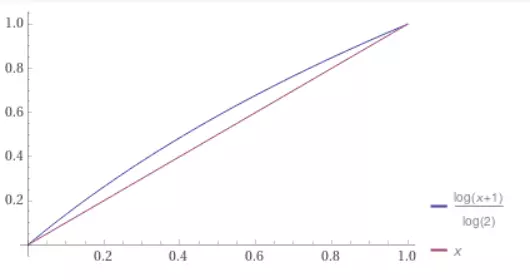
Vẽ lên đồ thị để thấy rõ hơn với σ = 0:

Người ta chứng minh được, với σ ≈ 0.0430357, sai số tuyệt đối sẽ nhỏ nhất.

Ta đổi phần thập phân sang dạng số tự nhiên, ta có:

Suy ra:

Xấp xỉ 1 trên căn 2 x

Ta có:

Dựa theo công thức xấp xỉ log ta có:

Suy ra:

Vì 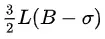là một hằng số, ta có thể dễ dàng tính được phần Ix một cách dễ dàng.

Phương pháp Newton

Ta sử dụng phương pháp Newton để tăng tính chính xác cho thuật toán. Xin đọc bài Newton's method Ta có công thức:

Tính đạo hàm ta có:

Theo công thức Newton, ta có:

Cài đặt thuật toán

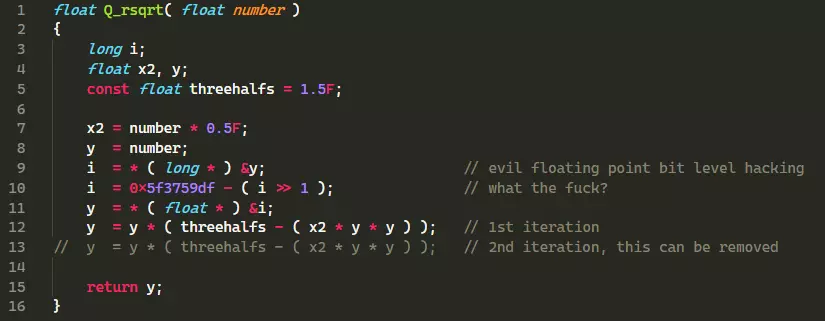
Thuật toán phiên bản trong Quake 3, ngôn ngữ C:

Nhìn vào đoạn code này, ta thấy nó không được sạch lắm ( sử dụng lại biến, không định nghĩa constant, ... ). Mình sẽ giải thích một số dòng không quen thuộc lắm nếu bạn chưa học C. Ở dòng 9, định nghĩa lại con trỏ kiểu float thành kiểu long trên cùng 1 vùng nhớ, ngược lại với dòng 11. Ở dòng 10, ta có phép toán dịch bit ( << ), sẽ làm giảm giá trị đi 1 nửa.

Các chỉ thị trên CPU liên quan

Vào năm 1999, bộ chỉ thị Streaming SIMD Extensions được thêm vào trên Intel Pentium III đi kèm theo đó là 2 chỉ thị rsqrtss & rsqrtps. 2 Chỉ thị này tính toán sấp xỉ các giá trị 1 trên căn x với độ chính xác chấp nhận được. Vì vậy sau này, người ta không còn thấy sự xuất hiện của thuật toán trên trong các phần mềm nữa.

Kết luận

Việc tính toán trong tin học luôn có những sự khác biệt với tư duy toán học thuần túy của chúng ta. Tuy nhiên những tính toán này đều dựa trên những biến đổi rất cơ bản và tự nhiên. Hy vọng các bạn thấy hay và bổ ích.