Rabin–Karp algorithm

String searching is one of the most common task done by people related to computer science. Almost everyday, there are some cases where they need to do string search. So there are intensive research going on that how we can efficiently search a pattern in a string till now. Previously we learned about KMP algorithm. Today we will learn about another algorithm named Rabin-Karp algorithm.

Rabin-Karp Algorithm

Rabin-Karp algorithm uses hashing to match a pattern in a string which is invented by Richard M. Karp and Michael O. Rabin in 1987. For a text T of length n and a pattern P of length m, the average case complexity of this algorithm is O(m+n). But in the Worst case, its complexity is same as brute-force algorithm. Though KMP is better to use for string search, Rabin-Karp is vastly used in plagiarism detecting softwares where sentences of a draft paper is matched against research paper in this world in a very short time.

Algorithm

If we see Brute-force approach, it takes O(mn) time to find a pattern in a string. What if we could compare two character in O(1) complexity like integer? Rabin-Karp algorithm gives us the previlage to convert a string to integer by hashing. We can convert a string to Base-B number, where B is equal to greater than highest ASCII value. Then again we need to convert this Base-B number to Base-10 number. we can do this by following

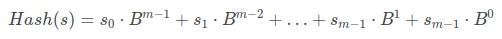
In this function s(i) is the ASCII value of i-th character of string s. We will get unique hash value for each unique string.

Determing Hash Value

So our prime task for implementing should be how efficiently we can find the hash value. At first we need to find the hash value of Pattern P. Then for each substring of m length in S, we need to match up. Now if we try to determine hash value h of each m-sized string, then the complexity will be O(mn). So this way wont give us any reason to use Brute-force approach. So we have to find a way to do it in O(n).

Lets say, H(i) is the hash value of m-sized substring of S starting from index i. We can write that like-

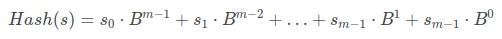
Lets say for m = 3, we can write H(0) and H(1) like this -

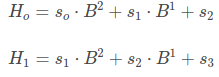
Now we can write H(1) in term of H(0) like -

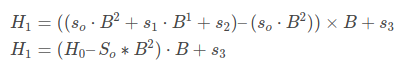
So, in general we can write -

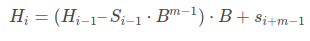
Now we can find hash of each m-sized substring in S in simple O(n) complexity. We just need to find the hash value of first m character. Others we can determine using hashing.

Implementation:

The ruby implementation of this algorithm is coded below

def rabin_karp text, pattern
    n = text.size
    m = pattern.size
    return -1 if n < m
    return -1 if m == 0 || n == 0
    b = 23
    power = b**(m - 1)
    hash_text = coverted_hash text, m, b
    hash_pattern = coverted_hash pattern, m, b
    return 0 if hash_text == hash_pattern
        
    (m...n).to_a.each do |i|
      hash_text -= power * text[i - m]
      hash_text *= B
      hash_text += text[i]
      return i - m + 1 if hash_text == hash_pattern
    end
    -1;
  end

  def converted_hash string, m, b
    h = 0
    power = 1
    i = m - 1
    until i >= 0 do
      h += s[i] * power;
      power *=  B
      i -= 1
    end
    h
  end

Complexity

In this implementation We find out hash value of pattern in O(m) complexity. And hash value of text in O(n). So the total complexity is O(m+n). But there is a possibility that the hash value can overflow. In that case we can modulo the value with a big number M. Again in that case hash value of two different string can be same. That can we can do rehashing with different base B and M. Or we can match character by character which will result complexity of O(mn). So it is actually better to use KMP in some cases.

Hope this will help you learn about the basics of Rabin-Karp algorithm. Thank you.