Knuth–Morris–Pratt(KMP) Algorithm

String is,without doubt, an non-ignorant part in programming. It is an envitable element in this computer science world. Finding for a defininite string or fully contained string is one of the burning job in computer science related work. Knuth–Morris–Pratt algorithm, in short KMP algorithm is a linear algorithm which will be broaden in this article.

Background

Lets think of a scenario - We get a String S = "I become so numb" and we need to search through for another string A = "numb" in S. What is the first approach to do this task? The most easiest one would be- starting from the 0-index of string S to find the find the first character of A. If it matches then check the next characters of A in S. The solution in ruby will be like -

def first_string_search s, a
    i = 0
    s_length = s.size
    a_length = a.size
    
    while i < s_length do
        next if s[i] != a[0]
        j = 1
        while i+j < s_length && j < a_length && s[i+j] == a[j] do
            j+= 1
            return i if j == a_length
        end
        i+= 1
    end
    false
end

if you observe the code, u can see that the complexity of this solution is O(mn) where m = length of s and n = length of a. Its Ok if both s and a is small in size. Think about the fact that they are enormous; what comes in your mind. Definitely the system will stand still. In careful thinking, we become astonished to learn that we can lookup any string in PDF reader or notepad or sublime in neglizible time, no matter how big the opened content is(may be 1000 page book). Minimum a day would be needed if we walk in that path. For finding a time-efficient solution, we will discover the KMP algorithm.

Knuth–Morris–Pratt Algorithm

in 1977, Donald Knuth, Vaughan Pratt and James H. Morris published an algorithm for string search which is known as KMP algorithm. In previous solution, we advanced by comparing each letter of a string. but in KMP algorithm it is tried to skip some letter- it is the basic idea

Algorithm steps are as follows

• At first we need to make a Pi table in terms of patter string P.
• After that we will check for patterns by the help of Pi table
• If any character is not matched, we can skip some characters based on pi table

Pi Table

This table is the helping array for KMP algorithm. The size of this table will be the size of pattern string P. Each element of this array will store the matched longest prefix or suffix of that string P.

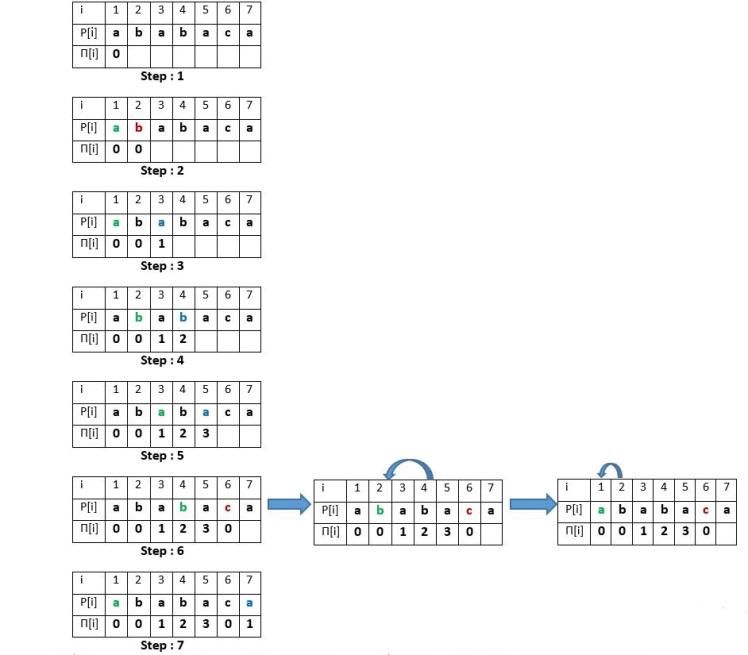
If you look at the picture above - for the first index of P the suffix and prefix is empty so we put 0 in that index.

• We will do the same for second index also.
• For third element of P, suffix = prefix = 1. So we put 1
• For fourth element of P, suffix = prefix = "ab" = 2. So we put 2 and so on

If we do it on code

def pi_table pattern
  f[0]=0
  j = 0
  m = pattern.size
  for i = 1; i < m; i++ do
    if pattern[i]==pattern[j]
      f[i]=j+1
      j += 1
    else
      while j!=0 do
        j = f[j-1]
        if pattern[i]==pattern[j]
            f[i] = j+1
            j+= 1
            break
        end
      end
    end
  end
end

Find Pattern using Pi table

Now we need to to find the pattern string P in reference string S. You can see the picture below

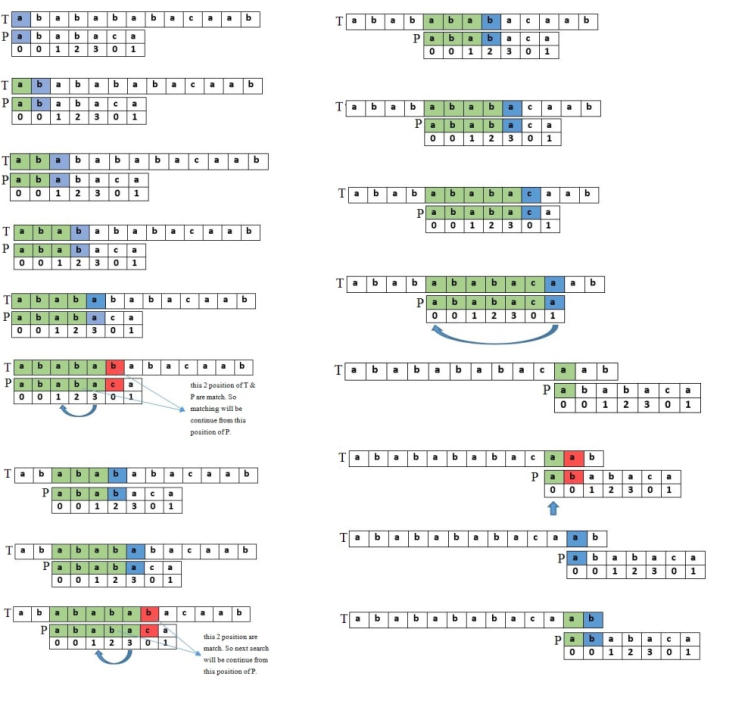
Finding a pattern in string S using the pi table is just like making the pi table above. If we get any difference in S and P, we can jump some character in S with the help of pi table because we already equaled the suffix and prefix. If we code this in ruby, we can write like this -

def kmp text, pattern
  j = 0
  for i = 0; i < n; i++ do
    if text[i]==pattern[j]
      if j==m-1
      return true if j==m-1
      j+= 1
    else
      while j!=0 do
        j = f[j-1]
        if text[i]==pattern[j]
          j+= 1
          break
        end
      end
    end
  end
  false
end

Complexity

For the pi table computation, the for loop is iterated m-1 times where m = size of pattern string P. The complexity of that part is O(m). And in KMP matching part, the loop runs n times where n = size of text S. So the time complexity for matching part is O(n). and the KMP algorithm runs in O(m+n)time complexity, which is more acceptable than O(mn) calculation of brute-force. The space complexity of this algorithm is O(m).

I wish the gyst from this post will make you interested to know more about search algorithms. Happy coding!!

Pic credit: Tanvir's Blog