Phần 2.Thuật toán QUY HOẠCH ĐỘNG

Bài đăng này đã không được cập nhật trong 4 năm

Thuật toán QUI HOẠCH ĐỘNG phần 2

Xin chào các bạn ở bài viết về QUI HOẠCH ĐỘNG phần 1:https://viblo.asia/p/phan-1thuat-toan-quy-hoach-dong-QpmleJzM5rd mình đã nói qua về qui hoạch động với những ví dụ đơn giản dễ hiểu.

Hôm nay mình xin đề cập đến một bài toán phức tạp hơn: Bài toán cái túi (Knapsack Problem)

Đây chỉ là một bài toán nhỏ để các bạn có thể vận dụng được những bài toán khó hơn hãy làm để hiểu thuần thục nó nhé.

Câu thần chú: Phân rã - Giải bài toán con - Tổng hợp bài toán con thành bài toán lớn

Mô tả bài toán

-Knapsack Problem là bài toán tên chộm mang theo một cái túi có dung lượng nhất định. Mục đích của tên chộm là chất đồ vật sao cho tổng trọng lượng không vượt quá dung lượng của cái túi và tổng giá trị lấy được là lớn nhất.

Cụ thể :

Có n đồ vật, đồ vật i có trọng lượng W_i và giá trị C_i

với $i = 1, 2, ..., n$ .

Tìm cách chất các đồ vật này vào cái túi có dung lượng là b sao cho tổng trọng lượng của các đồ vật được chất vào túi là không quá b, đồng thời tổng giá trị của chúng là lớn nhất.

Đi tìm lời giải bằng thuật toán qui hoạch động

Có: n - Số đồ vật, b - trọng lượng túi (lấy giá trị nguyên)

• Phân rã: Với các giá trị i (1..n) và L (0..b) Gọi MaxV(i,L) là tổng giá trị lớn nhất có thể chọn trong i đồ vật (từ 1 đến i) với trọng lượng tối đa của túi là L. Khi đó MaxV(n,b) là giá trị lớn nhất mang đi được.

• Giải bài toán con: MaxV(0,L) = 0 với mọi L, và MaxV(i,0) = 0 với mọi i.

• Tổng hợp:

Đã có MaxV(i-1,L): Giá trị lớn nhất mang đi được với i-1 đồ vật khi trọng lượng túi là L.
Xét đồ vật thứ i khi trọng lượng túi vẫn là L: Chỉ mang thêm đồ vật thứ i khi giá trị của túi lúc mang i-1 đồ vật ở trọng lượng túi là L - w * i (như thế mới đảm bảo mang thêm được đồ vật i có trọng lượng W_i khi trọng lượng túi là L ) cộng với giá trị của đồ vật thứ i, c[i] lớn hơn khi không mang đồ vật thứ i, MaxV(i-1,L). Bạn suy nghĩ 1 lúc phần này là ra ngay mà
Nghĩa là: $MaxV(i, L) = Max{MaxV(i-1,L-w[i])+c[i], MaxV(i-1,L)}$ tường minh quá rồi nhỉ :v

Giải thuật

    Procedure Bag_best
    {
    For L= 0 to b do MaxV[0,L] =0 ;

    For i= 0 to n do MaxV[i,0] =0 ;

    For i = 1 to n do

        For L = 1 to b do {

    MaxV[i,L] = MaxV[ i-1,L];

    If [(L >= w[i]) && (MaxV[i-1,L-w[i]]+c[i] > MaxV[i-1, L])]

    MaxV[i, L] = MaxV[i-1,L-w[i]]+c[i] ;
    }

    return MaxV(n, b) ;
    }

Một ví dụ cụ thể

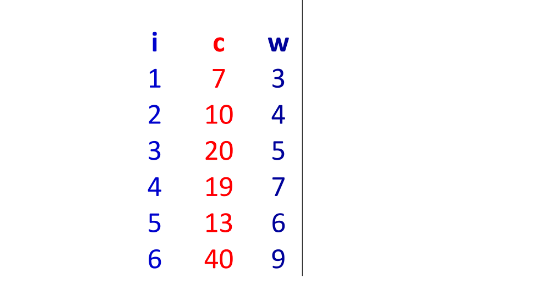
Cho 6 đồ vật (n = 6), và túi có trọng lượng b = 19. Các đồ vật có trọng lượng và giá trị như sau:

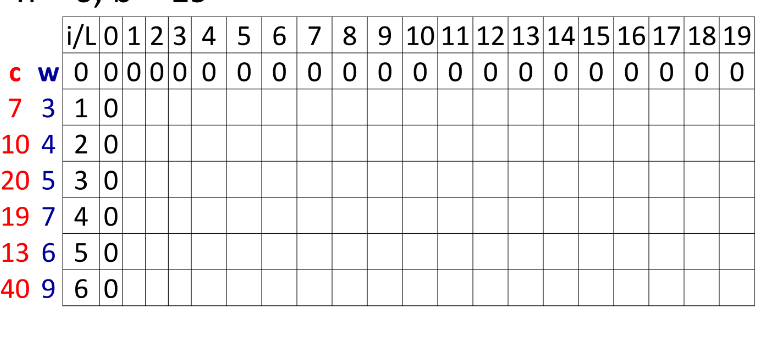
-Khởi tạo: MaxV[0,L] =0 , MaxV[i,0] =0

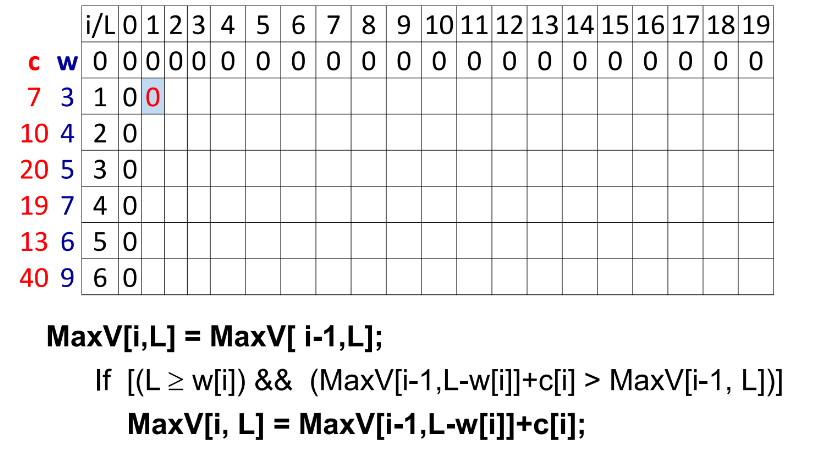
-Lặp : 2 vòng lặp như giải thuật ở trên

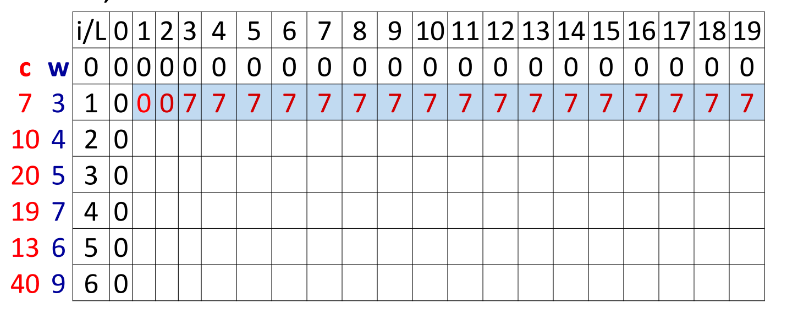
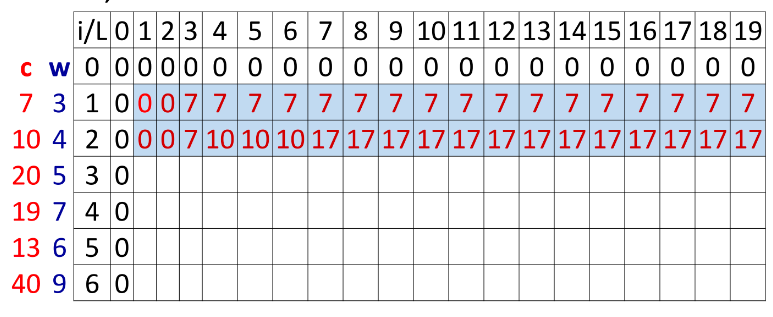
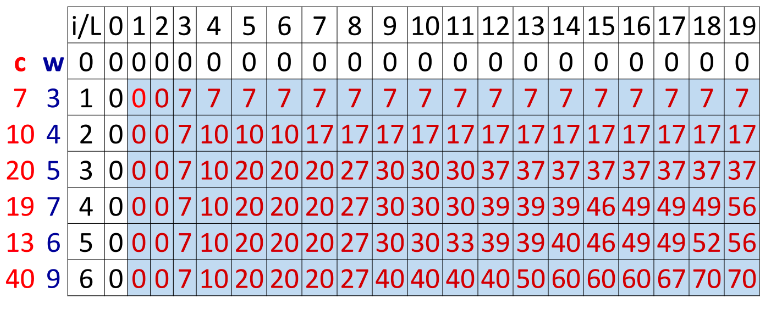
-Lặp đến hết ta được kết quả :

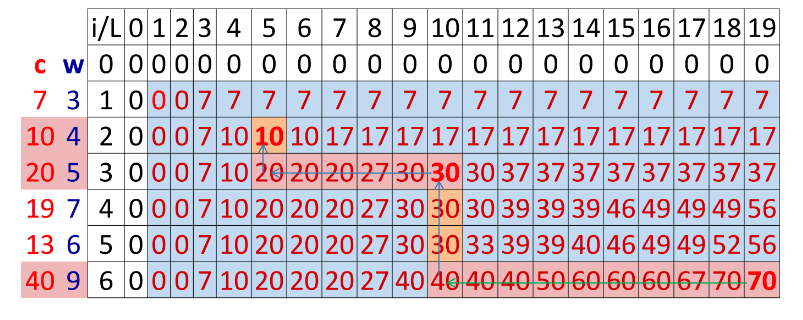
Những vật được mang đi: {2, 3, 6}
Tổng trọng lượng vật: 18
Tổng giá trị: 70

Kết luận

Công thức thần thánh là dây:

-Phân rã: Chia bài toán cần giải thành những bài toán con nhỏ hơn đến mức có thể giải trực tiếp được hay không? Nếu giải được chuyển sang bước giải bài toán con.

-Giải các bài toán con và ghi nhận lời giải: Lưu trữ lời giải của các bài toán con vào một bảng để sử dụng về sau.

-Tổng hợp lời giải:

Tổng hợp lời giải của các bài toán con kích thước nhỏ hơn để thành lời giải bài toán lớn hơn.
tiếp tục như vậy cho đến khi thu được lời giải của bài toán xuất phát (là bài toán con có kích thước lớn nhất)