vi
new
+23
Avatar
Nguyen Quynh Trang B @TrangQuynh
288 9 5
Đã đăng vào thg 4 30, 2021 8:47 CH 8 phút đọc
2.3K

Một số thuật toán sắp xếp

Chắc hẳn ngồi trên ghế giảng đường đại học thì ai cũng sẽ được làm quen với thuật toán. Nghe thì thật là trừu tượng và mơ hồ, nhưng để tối ưu hóa những bài toán đặt ra thì bắt buộc các bạn phải học đến nó. Mình xin chia sẻ 1 chút lí thuyết mà mình học được về các thuật toán sắp xếp đơn giản, mong là có thể giúp các bạn áp dụng vào bài toán thực tế của mình!

1. Thuật toán sắp xếp nổi bọt (Bubble Sort)

Ý tưởng

Đây có lẽ là loại sắp xếp quen thuộc nhất với mọi người.

  • Ban đầu tìm ra số lớn nhất và cho xuống cuối dãy: bằng cách so sánh và đổi chỗ 2 phần tử liền kề nhau từ phần tử đầu đến phần tử cuối.
    Lúc này coi như dãy số chỉ còn n-1 phần tử đầu, tiếp tục tìm ra số lớn nhất trong dãy giả định này như cách trên.
  • Tiếp tục đẩy dần số lớn nhất của dãy giả định hiện tại xuống cuối thì được dãy theo thứ tự bé đến lớn

Cài đặt thuật toán

for(int i = 0; i < n-1; i++){
		for (int j = 0; j < n – i – 1; j++)
			if (a[j] < a[j + 1]) swap (a[j], a[j + 1]);
		}
}

Ví dụ thuật toán

Sắp xếp mảng M có 5 phần tử [0, 8, 3, 4, 1]

i j M
0 [0,4) [0,8,3,4,1] -> [0,3,8,4,1] -> [0,3,4,8,1] -> [0,3,4,1,8]
1 [0,3) [0,3,4,1,8] -> [0,3,4,1,8] -> [0,3,1,4,8]
2 [0,2) [0,3,1,4,8] -> [0,1,3,4,8]
3 [0,1) [0,1,3,4,8]

Phân tích thuật toán:

  • Trong trường hợp tốt nhất: khi mảng ban đầu đã sắp xếp theo thứ tự tăng dần: Số phép hoán vị là Hmin = 0
  • Trong trường hợp xấu nhất: khi mảng ban đầu đã sắp xếp theo thứ tự giảm dần: Số phép hoán vị là Hmin = (N-1) + (N-2) + … + 1 = ½N(N-1)
  • Số phép hoán vị trung bình: Havg = ¼N(N-1)

Nhận xét về thuật toán nổi bọt

  • Thuật toán sắp xếp nổi bọt khá đơn giản, dễ hiểu và dễ cài đặt
  • Trong thuật toán sắp xếp nổi bọt, mỗi lần đi từ cuối mảng về đầu mảng thì phần tử nhẹ được trồi lên rất nhanh trong khi đó phần tử nặng lại chìm xuống chậm chạp do không tận dụng được chiều đi xuống (chiều đi từ đầu mảng về cuối mảng)
  • Thuật toán nổi bọt không phát hiện ra được các phần tử nằm hai đầu mảng đã nằm đúng vị trí chưa để có thể giảm bớt quãng đường đi trong mỗi lần đi
  • Nhược điểm: Hiệu suất thấp nhất

2. Thuật toán chia để trị (Merge Sort)

Ý tưởng

Ban đầu chia dãy làm đôi đến khi chỉ dãy con chỉ còn 1 phần tử. Sau đó merge các dãy lại với nhau đến khi được dãy có độ dài như ban đầu và đã được sắp xếp

  • Chia (Divide): Chia dãy gồm n phần tử cần sắp xếp thành 2 dãy, mỗi dãy có n/2 phần tử.
  • Trị (Conquer): Sắp xếp mỗi dãy con một cách đệ quy sử dụng sắp xếp trộn. Khi dãy chỉ còn một phần tử thì trả lại phần tử này.
  • Tổ hợp (Combine): Trộn (Merge) hai dãy con được sắp xếp để thu được dãy được sắp xếp gồm tất cả các phần tử của cả hai dãy con.

Cài đặt thuật toán

void mergeSort (int arr[], int l, int r)
{
    if (l < r)
    {
        int m = l + (r-l) / 2;
        mergeSort(arr, l, m);
        mergeSort(arr, m+1, r);
        merge(arr, l, m, r); // ghép dãy arr[l...m] và arr[m+1 ...r]
    }
}
void merge (int a[], int l, int m, int r)
{
    int n1 = m - l + 1; // kích thước mảng 1
    int n2 = r - m; // kích thước mảng 2
    
    int L[n1], R[n2]; // tạo 2 mảng tạm
    for (int i = 0; i < n1; i++) L[i] = arr [l+i];
    for (int i = 0; i < n1; i++) R[i] = arr [m+1+i];
    int i = 0, j = 0; // khởi tạo giá trị i, j cho vòng lặp while
    int k = l; //k là chỉ số của arr để bắt đầu lưu kết quả cần tìm
    while (i < n1 & j < n2)
    {
        if (L[i] < R [j]) 
        {
            arr[k] = L[i];
            i ++:
        }
        else 
        {
            arr[k] = R[j];
            j ++:
        }
        k++;
    }
    /*copy các phần tử còn lại của mảng L hoặc R vào arr nếu có. trường hợp nếu có là khi n1 != n2 */ 
    if (i < n1)
    {
        arr[k] = arr[i];
        i++;
        k++;
    }
    if (j < n2)
    {
        arr[k] = arr[j];
        j+;
        k++;
    }
}

Ví dụ thuật toán

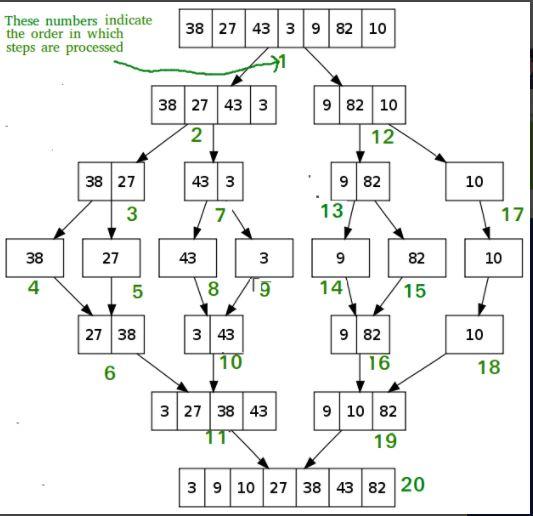
Sơ đồ sau đây từ Wikipedia cho thấy quy trình sắp xếp hợp nhất hoàn chỉnh cho một mảng mẫu [38, 27, 43, 3, 9, 82, 10]
Nếu chúng ta xem xét kỹ hơn sơ đồ, chúng ta có thể thấy rằng mảng được chia đệ quy làm hai nửa cho đến khi kích thước trở thành 1.
Khi kích thước trở thành 1, các quy trình hợp nhất sẽ hoạt động và bắt đầu hợp nhất các mảng trở lại cho đến khi mảng hoàn chỉnh đã hợp nhất.

Phân tích thuật toán

  • Độ phức tạp là O(nLogn) trong cả 3 trường hợp (xấu nhất, trung bình và tốt nhất) vì thuật toán luôn chia mảng thành hai nửa và mất thời gian tuyến tính để hợp nhất hai nửa.
  • So sánh chậm hơn với các thuật toán sắp xếp khác cho các nhiệm vụ nhỏ hơn.
  • Thuật toán sắp xếp hợp nhất yêu cầu thêm không gian bộ nhớ 0 (n) cho mảng tạm thời.
  • Nó đi qua toàn bộ quá trình ngay cả khi mảng được sắp xếp.
  • Ưu điểm: Hiệu suất của merge sort rất cao
  • Nhược điểm: Code thuật toán này khá phức tạp

3. Thuật toán sắp xếp nhanh (Quick Sort)

Ý tưởng

Chọn một phần tử trong mảng để làm điểm đánh dấu. Thuật toán sẽ thực hiện chia mảng thành các mảng con theo điểm mà mình đã chọn.
Có nhiều phiên bản quickSort khác nhau chọn pivot theo những cách khác nhau.

  • Luôn chọn phần tử đầu tiên làm trục.
  • Luôn chọn phần tử cuối cùng làm trụ (được triển khai bên dưới)
  • Chọn một phần tử ngẫu nhiên làm trục quay.
  • Chọn trung vị làm trục.

Cài đặt thuật toán

  • Chọn phần tử chốt.
  • Khai báo 2 biến con trỏ để trỏ để duyệt 2 phía của phần tử chốt.
  • Biến bên trái trỏ đến từng phần tử mảng con bên trái của phần tử chốt.
  • Biến bên phải trỏ đến từng phần tử mảng con bên phải của phần tử chốt.
  • Khi biến bên trái nhỏ hơn phần tử chốt thì di chuyển sang phải.
  • Khi biến bên phải nhỏ hơn phần tử chốt thì di chuyển sang trái.
  • Nếu không xảy ra trưởng hợp 5 và 6 thì tráo đổi giá trị 2 biến trái và phải.
  • Nếu trái lớn hơn phải thì đây là giá trị chốt mới.
void swap (int *a, int *b) {
	int temp=*a;
	*a=*b;
	*b=temp;
}
int partition (int arr[],int l,int h){
	int x=arr[h];
	int i=l-1;
	for (int j=l; j<=h-1; j++) {
		if(arr[j]<=x) {
			i++;
			swap(&arr[i], &arr[j]);
		}
	}
	swap(&arr[i+1], &arr[h]);
	return(i+1);
}
void quicksort (int arr[],int l,int h){
	if(l<h) {
		int p=partition(arr,l,h);
		quicksort (arr, l, p-1);
		quicksort (arr, p+1, h);
	}
}

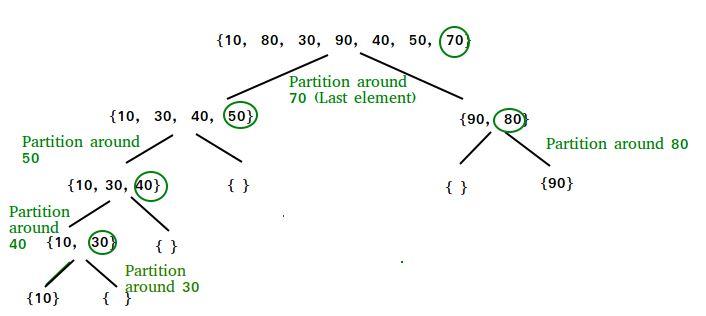
Ví dụ

Phân tích thuật toán

  • Độ phức tạp thuật toán của quick sort
    Trường hợp tốt: O(nlog(n))
    Trung bình: O(nlog(n))
    Trường hợp xấu: O(n^2)
  • Không gian bộ nhớ sử dụng: O(log(n))
  • Ưu điểm: Tuỳ cách chọn pivot mà tốc độ của thuật toán nhanh hay chậm
  • Nhược điểm: Code khá phức tạp

4. Tổng kết

Trên đây là một số những thuật toán sắp xếp mình đã tìm hiểu, nếu có gì sai sót, bạn góp ý cho mình nhé. Hi vọng bài viết này có ích với bạn. Hẹn gặp lại bạn ở những bài viết tiếp theo.

5. Tài liệu tham khảo

https://www.geeksforgeeks.org/merge-sort/
https://www.geeksforgeeks.org/quick-sort/

Education MobileTeam

All rights reserved

Mục lục


Viblo
Hãy đăng ký một tài khoản Viblo để nhận được nhiều bài viết thú vị hơn.
Đăng kí