Các kiến thức trong bài viết hôm nay bao gồm:

• Core idea của bài toán Face Recognition
• FaceNet with Triplet Loss
• CosFace
• ArcFace

1. Bài toán Face Recognition

Chắc hẳn mọi người đều đã từng nghe đến bài toán Face Recognition. Face Recognition có thể nói bao gồm hai bài toán con:

• Face identification (nhận diện khuôn mặt): là bài toán one-to-many. Input là ảnh một khuôn mặt, và mô hình của chúng ta cần trả lời câu hỏi "người này là ai", như vậy, output là nhãn tên của người trong ảnh.
• Face vertification (xác thực khuôn mặt): là bài toán one-to-one. Mô hình cần trả lời câu hỏi, hai người này có phải cùng một người.

Trong bài viết này, mình sẽ bàn về các phương pháp tiếp cận bài toán nhận diện khuôn mặt (như ảnh trên).

Có thể phân thành 2 cách tiếp cận:

1.1 One-shot learning

Về cơ bản, ta có thể coi đây là bài toán có input là dữ liệu ảnh và output là nhãn tên 1 ngoài, tức là bài toán classification. Vậy nên ta có thể xây dựng một kiến trúc CNN classify để predict người đó là ai.

Nhược điểm của phương pháp này là chỉ cần xuất hiện thêm người mới, chúng ta phải huấn luyện lại toàn bộ mô hình (shape của output thay đổi tăng lên 1). Đối với các bài toán châm công hay camera an ninh khu chung cư, điều này gây bất lợi rất lớn, vì số lượng người luôn biến động theo thời gian.

Để khắc phục được vấn đề này, chúng ta sử dụng phương pháp learning similarity.

1.2 Learning Similarity

Giống như ý tưởng của các thuật toán phân cụm, hiểu một cách đơn giản, hai ảnh càng giống nhau (cùng 1 người), thì khoảng cách giữa chúng càng bé, và ngược lại, hai ảnh càng xa nhau thì khoảng cách càng phải lớn. Khoảng cách ở đây có thể là Norm chuẩn L1 hoặc L2 (euclidean distance).

$\left\{\begin{matrix} d ( img1, img2) \leqslant T & \rightarrow same \\ d ( img1, img2) > T & \rightarrow different \end{matrix}\right.$

Với cách tiếp cận này, ta thường định nghĩa một ngưỡng threshold. Ta sẽ so sánh ảnh input với tất cả các ảnh trong dataset, và nếu khoảng cách nằm dưới ngưỡng cho phép, ta sẽ lấy các ảnh đó làm output. (như vậy kết quả trả về có thể một hoặc nhiều ảnh, cách đơn giản nhất là tìm nhãn phổ biến nhất trong tập nhãn output (ý tưởng của k-NN)).

Vậy so với one-shot learning, phương pháp này có ưu điểm không bị phụ thuộc vào số lượng classes, không cần phải huấn luyện lại khi xuất hiện class mới.

Vấn đề tiên quyết của phương pháp này, là làm sao để có một mô hình embedding đủ tốt, để embed các ảnh thành 1 vector. Thông thường, các mô hình cần tìm cách embed 1 ảnh xuống còn 1 vecto 512 hoặc 128 chiều, vừa đủ nhỏ để tính toán, lại vừa biểu diễn được đủ thông tin của ảnh.

Ta cần tới mô hình Siamese Network.

Siamese Network

Siamese network được xây dựng dựa trên base network là một CNN architecture (Resnet, Inception, InceptionResnet, MobileNet, vv) đã được loại bỏ output layer, có tác dụng encoding ảnh thành véc tơ embedding.

Đầu vào của mạng Siamese network là 2 bức ảnh bất kì được lựa chọn ngẫu nhiên từ dữ liệu ảnh. Output của Siamese network là 2 véc tơ tương ứng với biểu diễn của 2 ảnh input. Sau đó chúng ta đưa 2 véc tơ vào hàm loss function để đo lường sự khác biệt giữa chúng.

Có thể thấy, việc lựa chọn hàm loss function quyết định rất nhiều tới độ chính xác của mô hình.

Bài viết hôm nay, mình sẽ bàn về một số Loss Function của Face Recognition.

Face Recognition Loss Function

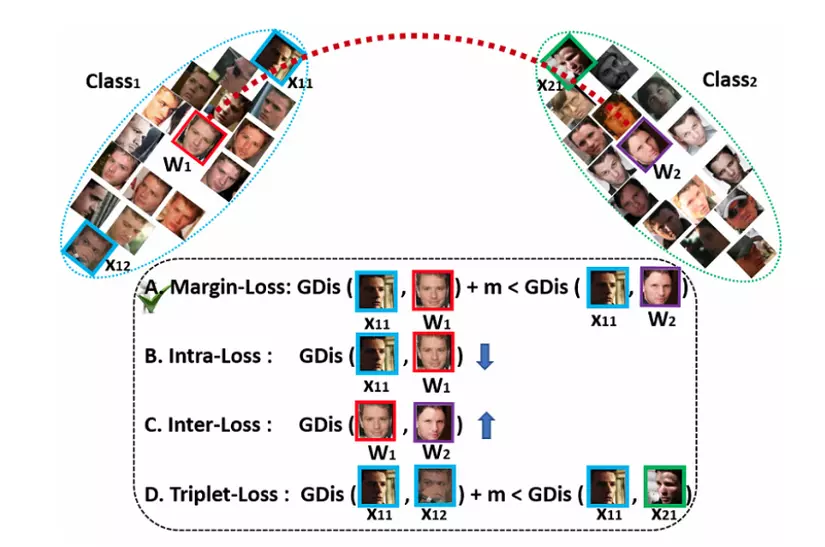
Hãy nhìn vào hình sau:

Có thể thấy ta có 4 loại ở đây:

• Margin-Loss: thêm margin giữa sample và centres,. có thể kể đến CosFace và ArcFace mà mình sẽ giới thiệu ở phần 3 và 4.
• Intra-Loss: giảm khoảng cách giữa mẫu và centre tương ứng.
• Inter-Loss: tăng khoảng cách giữa các centres khác nhau.
• Triplet-Loss: thêm margin vào giữa các mẫu bộ ba (triplet samples).

Và đanh thép hơn, paper ArcFace tuyên bố các chiến lược thuộc loại Margin-Loss mới là hiệu quả nhất. Nhưng thôi mình cứ từ từ, xem xét từng loại một nhé.

Let's start!

2. Facenet with Triplet Loss

Mình đã viết được hơn một nửa phần này cho đến khi đọc được một bài viết tiếng việt của tác giả Phạm Đình Khánh. (vì facenet đã xuất hiện từ lâu nên cũng có nhiều bài viết tiếng anh đầy đủ nhưng vì đây là blog tiếng việt, mình ưu tiên tìm kiếm các bài viết tiếng việt cho mọi người).

Bài viết bao gồm đầy đủ các công thức toán và cũng được giải thích rất dễ hiểu. Cảm ơn tác giả Phạm Đình Khánh. Mọi người có thể đọc nó ở đây:

• FaceNet with TripleLoss - PhamDinhKhanh Blog

Link paper gốc:

• FaceNet: A Unified Embedding for Face Recognition and Clustering https://arxiv.org/pdf/1503.03832.pdf

Nếu bạn đã đọc đến dòng này, hi vọng bạn đã hiểu đc core idea của Triplet Loss.

Về cơ bản, triplet-loss-based methods gặp phải hai vấn đề như sau:

• Một là, nếu dataset càng ngày càng lớn, sẽ có sự bùng nổ về số lượng bộ ba triplet samples, dẫn để sự lặp lại đáng kể các bước.
• Hai là, nếu bạn đã hiểu về facenet, sẽ biết việc tìm ra các bộ semi-hard samples không phải chuyện đơn giản.

Mình xin phép trích dẫn như trên và dành thời gian bài viết cho CosFace và ArcFace, được ra rời sau và được đánh giá là vượt trội hơn facenet.

3. CosFace

• Link paper gốc: CosFace: Large Margin Cosine Loss for Deep Face Recognition

Hình sau khái quát các phase trong traning và testing CosFace.

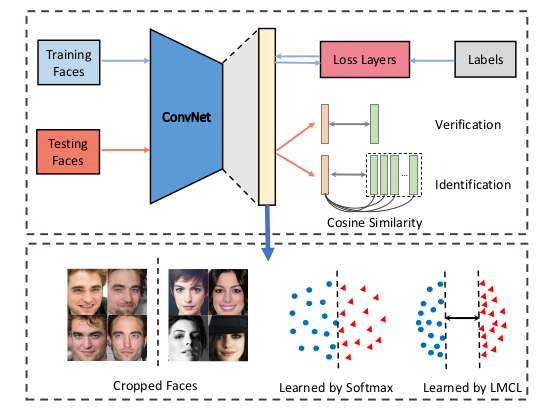
Hình 1

• Large Margin Cosine Loss (LMCL), hay còn gọi là CosFace, được cải tiến dựa trên softmax loss, nên mình sẽ nhắc lại về sofmax một chút.

Softmax Loss Function

• Nếu bạn chưa biết về Norm, có thể đọc ở đây: Norm (chuẩn) - ML cơ bản.

  Các kiến thức bao gồm: Norm là gì? Norm 2? Norm của ma trận là gì? (Norm Frobenius)

• Nếu bạn chưa biết về Softmax, có thể đọc ở đây (rất đầy đủ toán): Softmax Regression - ML cơ bản. Mình xin phép tóm tắt một số ý cơ bản sau đây.

Hầu hết các bạn học machine learning đều đã học qua Softmax Regression, một trong hai thuật toán classification thường xuyên được sử dụng nhất (cùng với SVM). Đặc biệt, softmax còn thường được dùng để đưa ra output cuối trong các mạng neural network.

Ban đầu, nếu bạn còn nhớ Logistic Regression, thì đây là thuật toán classification với 2 nhãn. Câu hỏi đặt ra là nếu có nhiều hơn 2 nhãn thì sao. Một số phương pháp được đưa ra như: one-vs-one (so sáng từng cặp nhãn một), one-vs-rest (một và các nhãn còn lại), one-hot. Mỗi phương pháp đều có ưu và nhược riêng. Tuy nhiên, ta vẫn cần một hàm tổng quát hơn cho bài toán nhiều nhãn.

Các điều kiện hàm này cần thỏa mãn bao gồm:

• Có thể đưa ra một phân phối xác suất cho tất cả các nhãn. $a_{i}$ là xác suất input rơi vào class $i$

• Các $a_{i}$ phải dương và tổng các $a_{i}$ phải bằng 1 (phân phối xác suất mà :vv)

• Giá trị $z_{i}={w_{i}}^{T}x$ càng lớn thì xác suất dữ liệu rơi vào class i càng cao -> cần một hàm đồng biến. Đồng thời, lưu ý rằng $z_{i}$ có thể âm hoặc dương, nhưng ta hi vọng một hàm số đơn giản có thể làm $z_{i}$ dương, và đồng biến, nên ta chọn hàm $exp(z_{i}) = e^{z_{i}}$.

  Cuối cùng, ta có softmax function:

$$a_{i}=\frac{exp(z_{i})}{\sum_{j=1}^{C}exp(z_{j})}, \forall i = 1,2,...,C$$

Như vậy, với mỗi đầu vào x, output sẽ là một phân phối xác suất $a=softmax(W^{T}x)$, nhưng nhãn thực sự lại là một one-hot encoding y (các vị trí khác bằng 0, vị trí truth class bằng 1). Vậy hàm Loss sẽ được xây dựng để tối thiểu sự khác nhau giữa đầu ra dự đoán a và đầu ra thực sự y. Thông thường ta có thể nghĩ tới:

$$J(W)= \sum_{i=1}^{N}\begin{Vmatrix}a_{i}-y_{i} \end{Vmatrix}_{2}^{2}$$

Tuy nhiên đây không hẳn là một hàm loss tốt để so sánh 2 phân bố xác suất. Thay vào đó, ta dùng cross entropy.

Cross entropy giữa hai phân phối p và q (với p và q rời rạc, như a và y) được định nghĩa là:

$$H(p,q)=-\sum_{i=1}^{C}p_{i}log(q_{i})$$

Như vậy, trong bài toán softmax regression, chúng ta có softmax los function là:

$$J(W;x_{i},y_{i})=-\sum_{j=1}^{C}y_{ij}log(a_{ij})$$

Đầy đủ hơn nữa, kết hợp tất cả các cặp dữ liệu $x_{i}$, $y_{i}$, $\forall i = 1,2,...,N$ và $\forall j = 1,2,...,C$, chúng ta sẽ có hàm mất mát cho Softmax Regression như sau:

$$J(W;x_{i},y_{i})=-\sum_{i=1}^{N}\sum_{j=1}^{C}y_{ij}log(a_{ij})=-\sum_{i=1}^{N}\sum_{j=1}^{C}y_{ij}log(\frac{e^{(w_{j}^{T}x_{i})}}{\sum_{k=1}^{C}e^{(w_{k}^{T}x_{i})}})$$

Trông hơi hổ báo quá, nên mình xin phép viết gọn lại một chút, theo đúng format của paper CosFace cho mọi người dễ theo dõi.

$$L_{s}=\frac{1}{N} \sum_{i=1}^{N}-\log p_{i}=\frac{1}{N} \sum_{i=1}^{N}-\log \frac{e^{f_{y_{i}}}}{\sum_{j=1}^{C} e^{f_{j}}}$$

Trong đó:

$$f_{j}= W_{j}^{T}x = \left \| W_{j} \right \|\left \| x \right \|cos \theta _{j}$$

Có thể thấy, norm(W) và góc giữa các vector ảnh hưởng tới phân bố xác suất cuối cùng.

Để học feature được hiệu quả, norm(W) cần phải bất biến, (?) vì vậy paper cố định norm (W) = 1 (bằng L2 Nomarlization).

Trong testing, paper so sánh vectơ đặc trưng của hai khuôn mặt bằng cách sử dụng cosine similarity. (xem ảnh) Ta có thể thấy, norm của vectơ đặc trưng không đóng bất kỳ vai trò nào đối với hàm tính điểm. Vì vậy, trong khi training, chúng ta có thể cố định norm (x) = s. Vì vậy, phân phối xác suất cuối cùng chỉ phụ thuộc vào cosin của góc và do đó Loss function trở thành:

$$L_{n s}=\frac{1}{N} \sum_{i}-\log \frac{e^{s \cos \left(\theta_{y_{i}, i}\right)}}{\sum_{j} e^{s \cos \left(\theta_{j, i}\right)}}$$

Đây chính là Normalized Version of Softmax Loss (NSL).

Tuy nhiên, NSL vẫn chưa đủ tốt. Paper đề xuất thêm Cosine Margin (m).

Ta có một ví dụ như sau: nếu C=2 (2 class), $\theta$ là góc giữa weight và feature vecture. NSL yêu cầu $\cos (\theta 1)>\cos (\theta 2)$ khi C1 là truth class.

Giờ ta thêm vào một margin (m), và yêu cầu $\cos (\theta 1)-\mathrm{m}>\cos (\theta 2)$, trong đó m ≥ 0 là một parameter cố định được đưa vào để điều khiển độ lớn của cosine margin.

Đây chính là Large Margin Cosine Loss LMCL, hay còn gọi là CosFace.

$$L_{l m c}=\frac{1}{N} \sum_{i}-\log \frac{e^{s\left(\cos \left(\theta_{y_{i}, i}\right)-m\right)}}{e^{s\left(\cos \left(\theta_{y_{i}, i}\right)-m\right)}+\sum_{j \neq y_{i}} e^{s \cos \left(\theta_{j, i}\right)}}$$

theo điều kiện,

$$W=\frac{W^{*}}{\left\|W^{*}\right\|}$$

$$x =\frac{x^{*}}{\left\|x^{*}\right\|}$$

$$\cos \left(\theta_{j}, i\right) = W_{j}^{T} x_{i}$$

Okayy, dài dòng thế cũng không bằng một hình ảnh tường minh.

$$(Hình 2)$$

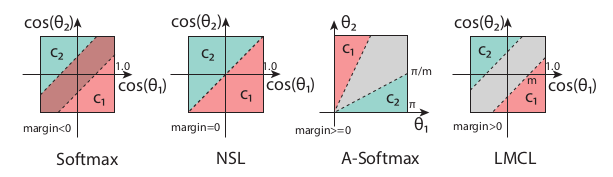
Trong hình trên, ta có thể thấy ảnh hưởng của giá trị margin tới quyết định phân loại. Bằng cách tìm ra margin thích hợp, ta sẽ có một mô hình tốt hơn. Theo 4 trường hợp của margin, ta có 4 loại Loss Function.

• Softmax:

$$\left\|W_{1}\right\| \cos \left(\theta_{1}\right)=\left\|W_{2}\right\| \cos \left(\theta_{2}\right)$$

Nhược: biên phụ thuộc vào cả độ lớn của vectơ trọng số và góc, do đó biên quyết định bị chồng lên nhau trong không gian cosin.

• NSL

$$\cos (\theta 1)=\cos (\theta 2)$$

Nhược: yếu với noise.

• A-Softmax

$$\begin{aligned}&C_{1}: \cos \left(m \theta_{1}\right) \geq \cos \left(\theta_{2}\right) \\ &C_{2}: \cos \left(m \theta_{2}\right) \geq \cos \left(\theta_{1}\right)\end{aligned}$$

Nhược: biên trở nên nhỏ hơn khi $\theta$ giảm và biến mất hoàn toàn khi θ = 0.

• LMCL (CosFace)

$$\begin{aligned}&C_{1}: \cos \left(\theta_{1}\right) \geq \cos \left(\theta_{2}\right)+m \\ &C_{2}: \cos \left(\theta_{2}\right) \geq \cos \left(\theta_{1}\right)+m \end{aligned}$$

Ưu: mạnh hơn kể cả khi có một ít nhiễu, nhất quán với mọi mẫu bất kể góc của weight vectors.

Feature Normalization

Đây là một phần nữa paper của CosFace có đề cập đến. Hãy nhìn lại một chút, trong các bước biến đổi phía trên, chúng ta đã normalized norm(W)=1 và norm(x) = s. Kết quả, feature vectors giờ phân phối trên một hypersphere (hình cầu n-chiều), trong khi the scaling-parameter s kiểm soát độ lớn của bán kính.

• Vậy câu hỏi là: tại sao ta lại feature normalization cho việc huấn luyện mô hình theo CosFace Loss ?

Có thể thấy, Softmax loss ban đầu mà không có feature normalization sẽ học được cả chuẩn Euclide (L2-norm) của vectơ đặc trưng và giá trị cosin của góc. Ngược lại, LMCL yêu cầu toàn bộ tập các feature vectors phải có cùng L2-norm, sao cho việc học chỉ phụ thuộc vào các giá trị cosin, tăng hiệu quả phân biệt. Khi đó, các feature vectors từ các class giống nhau được nhóm lại với nhau và các vectors từ các clall khác nhau được tách ra trên bề mặt của siêu cầu hypersphere.

Hình ảnh dưới đây cho thấy rõ ảnh hưởng của việc có thêm W trong sự phân tách các vectors trên bề mặt hypersphere.

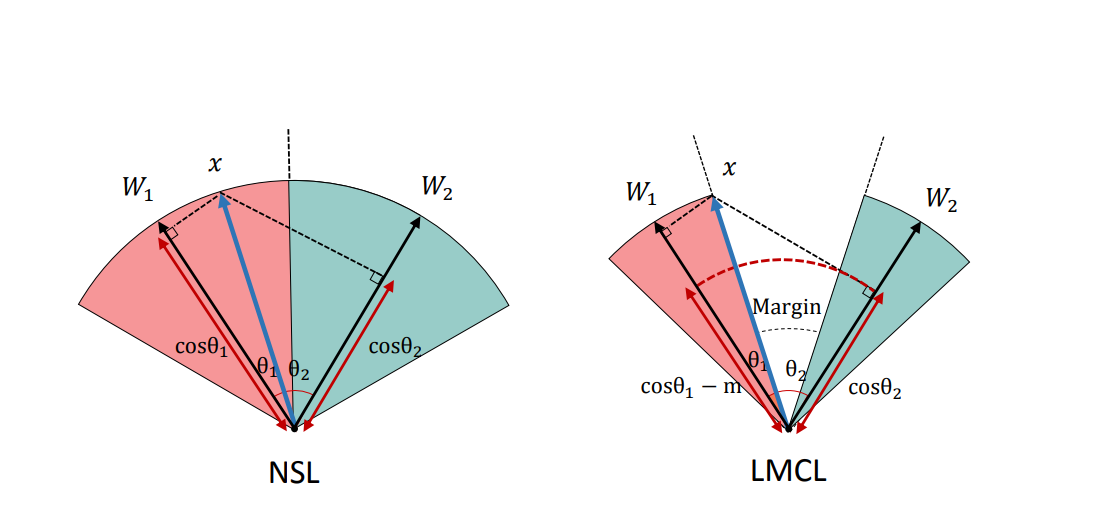
• Câu hỏi tiếp theo là: vậy giá trị của 's' là bao nhiêu?

Thực ra mình cx ko hiểu phần này lắm, lúc nào hiểu mình sẽ cập nhật. Paper đưa ra một công thức như sau:

$$s \geq \frac{C-1}{C} \log \frac{(C-1) P_{W}}{1-P_{W}}$$

• Câu hỏi cuối: Ảnh hưởng của cosine margin 'm'?

Chọn m như thế nào cho tối ưu. Một lựa chọn hợp lý của $m ∈ [0, C / (C-1)]$ với C là số classes. (đọc thêm paper để rõ về công thức trên). Đại ý là, m càng lớn, khả năng phân biệt càng cao. Tuy nhiên, thực tế, mô hình không hội tụ khi m quá lớn, vì ràng buộc cosin (tức là $cos θ1 −m> cos θ2$ hoặc $cos θ2 −m> cos θ1$ đối với trường hợp 2 classes) trở nên chặt chẽ hơn và khó được thỏa mãn. Bên cạnh đó, ràng buộc cosine với m quá lớn buộc quá trình huấn luyện phải nhạy cảm hơn với dữ liệu nhiễu. M ngày càng tăng bắt đầu làm giảm hiệu suất tổng thể tại một số điểm, là nguyên nhân không hội tụ.

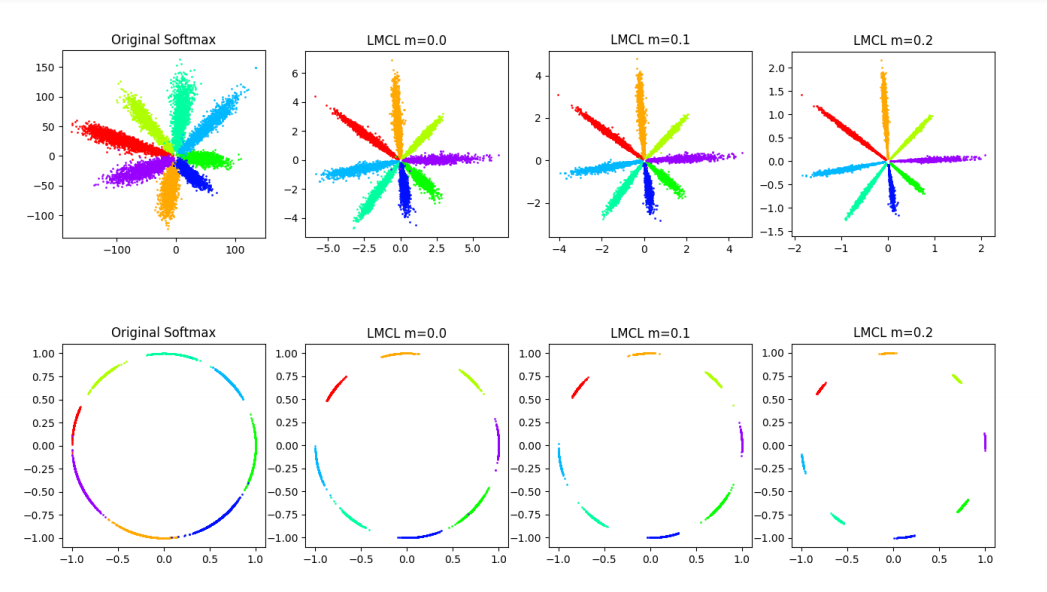
Vậy, đó là CosFace. Tiếp theo, mình sẽ xin phép giới thiệu về ArcFace.

4. ArcFace

Wow, nếu đã đọc đến tận đây, giờ thì dễ hiểu hơn một chút rồi.

Bởi vì Additive Angular Margin Loss , hay còn gọi là ArcFace, cũng được cải tiến dựa trên softmax loss function.

Link paper gốc:

• ArcFace: Additive Angular Margin Loss for Deep Face Recognition https://arxiv.org/pdf/1801.07698.pdf

Source code official:

• https://github.com/deepinsight/insightface

Paper của ArcFace có một đoạn so sánh với tiền nhiệm của nó , SphereFace và CosFace như sau: (mình để tiếng anh cho dễ hiểu)

Even though SphereFace [18] introduced the important idea of angular margin, their loss function required a series of approximations in order to be computed, which resulted in an unstable training of the network. In order to stabilize training, they proposed a hybrid loss function which includes the standard softmax loss. Empirically, the softmax loss dominates the training process, because the integer-based multiplicative angular margin makes the target logit curve very precipitous and thus hinders convergence.

CosFace [37, 35] directly adds cosine margin penalty to the target logit, which obtains better performance compared to SphereFace but admits much easier implementation and relieves the need for joint supervision from the softmax loss.

Một hình ảnh cực kỳ rõ nét và tường minh do paper cung cấp.

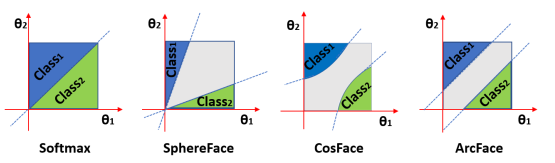
(lúc đầu nhìn qua mình kiểu, ủa, sao visualization của CosFace ở đây trông lạ lạ so với Hình 2 phía trên, rồi nhìn lại lần nữa mới nhạn ra là hai hình khác hệ quy chiếu. )

Ta có hàm softmax loss thông thường:

$$L_{1}=-\frac{1}{N} \sum_{i=1}^{N} \log \frac{e^{W_{y_{i}}^{T} x_{i}}}{\sum_{j=1}^{n} e^{W_{j}^{T} x_{i}}}$$

Tương tự như đã làm trong CosFace, để cho đơn giản, weight được normalized = 1 bằng cách sử dụng L2 Normalization. Đưa về $W_{j}^{T}x = \left \| W_{j} \right \|\left \| x \right \|cos \theta _{j}$ Feature cũng được L2 normalized và re-scaled về bằng s. Bước chuẩn hóa này giúp predictions chỉ phụ thuộc vào góc giữa features và weight.

Ta được LMCL (CosFace):

$$L_{2}=-\frac{1}{N} \sum_{i=1}^{N} \log \frac{e^{s \cos \theta_{y_{i}}}}{e^{s \cos \theta_{y_{i}}}+\sum_{j=1, j \neq y_{i}}^{n} e^{s \cos \theta_{j}}}$$

Vì các embedding features được phân phối xung quanh mỗi feature centre trên hypersphere (hình cầu trong không gian n-chiều), paper đề xuất thêm thêm một additive angular margin penalty m giữa $x_{i}$ và $W_{yi}$ để đồng thời tăng cường độ nhỏ gọn trong nội bộ class và sự khác biệt giữa các class.

$$L_{3}=-\frac{1}{N} \sum_{i=1}^{N} \log \frac{e^{s\left(\cos \left(\theta_{y_{i}}+m\right)\right)}}{e^{s\left(\cos \left(\theta_{y_{i}}+m\right)\right)}+\sum_{j=1, j \neq y_{i}}^{n} e^{s \cos \theta_{j}}}$$

Và kết quả, chúng ta được:

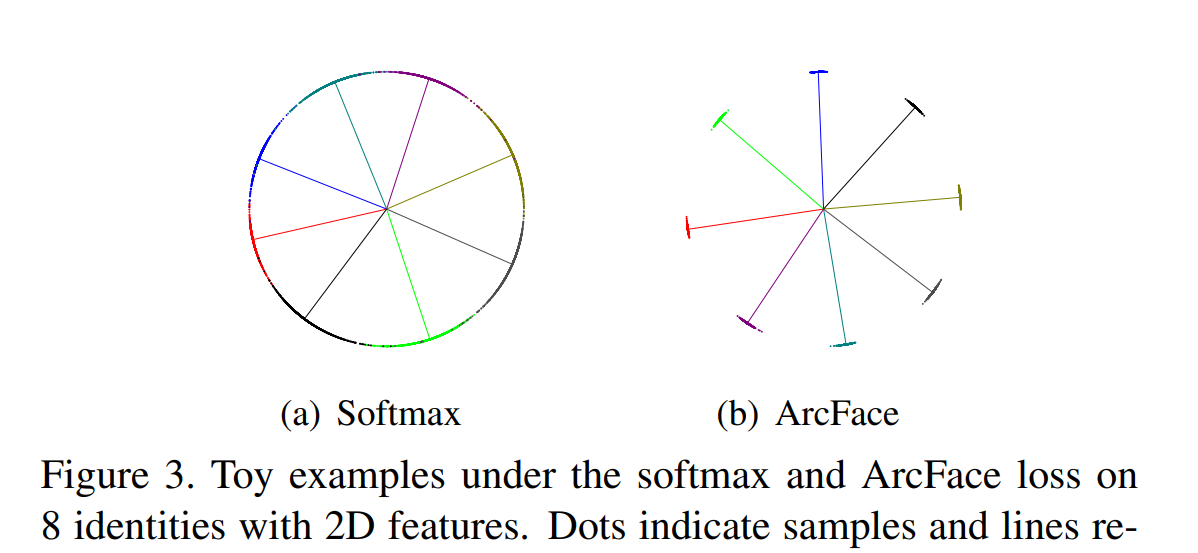
Bây giờ, hãy cùng xem quá trình training một DCNN bằng ArcFace.

(mọi người có thể vào paper để xem ảnh nét nhất có thể, và kèm theo Pseudo-code khá chi tiết nữa).

Đại ý các bước là:

• Sau khi normalization weights và feature vectors, ta lấy được $cos\theta_{j}$ với $\forall j = 1,2,...,C$ (C là số class).

• Ta cần tính $\theta_{j}$ (rất ez, lấy arccos là được). $\theta_{j}$ là góc giữa ground truth weight $W_{yi}$ và feature vector $x_{i}$.

• Sau đó ta tính $cos(\theta+m)$. Nếu bạn còn nhớ vòng tròn lượng giác, thì trong khoảng từ 0 đến $\pi$, góc càng tăng cos càng giảm.

• Tính $s* cos(\theta+m)$ . Sau đó đưa vào softmax để lấy ra phân phối xác suất probability của các nhãn.

• Cuối cùng, ta có ground truth vector (là label đã được one-hot) cùng probability, đóng góp vào cross entropy loss.

• Phần còn lại của paper ArcFace bao gồm các so sánh ArcFace với các loại Loss khác, thử nghiệm kết hợp 3 loại Margin-loss (multiplicative angular margin của SphereFace, additive angular margin của ArcFace và additive cosine margin của CosFace (cho kết quả tốt hơn)), cùng các kết quả thử nghiệm trên các bộ dataset và benchmark khác nhau.

• Bonus cuối paper, tại sao lại chọn số chiều của embedding features là 512-d?

Link paper gốc:

• ArcFace: Additive Angular Margin Loss for Deep Face Recognition

Một paper nữa cải tiến hơn cùng nhóm tác giả:

• Sub-center ArcFace: Boosting Face Recognition by Large-scale Noisy Web Faces

Paper của SphereFace nếu các bạn muốn đọc:

• SphereFace: Deep Hypersphere Embedding for Face Recognition

5. Kết

Bài đã dài rồi. Vì mình cũng ko phải là người giỏi Toán và cũng mới tập tành đọc paper, nên có thể bài viết còn nhiều thiếu sót. Mong nhận được góp ý và sửa lỗi từ mọi người thông qua mục comment của viblo hoặc qua gmail: ngthanhhuyen1707@gmail.com.

Nếu bài viết hữu ích, cho mình xin một upvote để có thêm động lực nhá ^^

Cảm ơn các bạn đã theo dõi ^^